Article

REVIEW: 50+ Years of Protein Folding

A. V. Finkelstein

Institute of Protein Research, Russian Academy of Sciences, 142290 Pushchino, Moscow Region, Russia; E-mail: afinkel@vega.protres.ru

Received May 25, 2017; Revision received July 10, 2017
The ability of proteins to spontaneously form their spatial structures is a long-standing puzzle in molecular biology. Experimentally measured rates of spontaneous folding of single-domain globular proteins range from microseconds to hours: the difference – 10-11 orders of magnitude – is the same as between the lifespan of a mosquito and the age of the Universe. This review (based on the literature and some personal recollections) describes a winding road to understanding spontaneous folding of protein structure. The main attention is given to the free-energy landscape of conformations of a protein chain – especially to the barrier separating its unfolded (U) and the natively folded (N) states – and to physical theories of rates of crossing this barrier in both directions: from U to N, and from N to U. It is shown that theories of both these processes come to essentially the same result and outline the observed range of folding and unfolding rates for single-domain globular proteins. In addition, they predict the maximal size of protein domains that fold under solely thermodynamic (rather than kinetic) control, and explain the observed maximal size of “foldable” protein domains.
KEY WORDS: protein folding rate, Levinthal’s paradox, folding funnel, free-energy landscape, phase separation, free-energy barrier, detailed balance law, protein secondary structure formation and assembly
DOI: 10.1134/S000629791814002X

Protein folding is a physical process during which a protein chain acquires its native (biologically functional) spatial structure “by itself”.

The spontaneous folding phenomenon was discovered by Anfinsen’s group in 1961 [1] on the example of spontaneous restoration of biochemical activity and “correct” S–S bonds in vitro in bovine ribonuclease A after its complete (including elimination of all S–S bonds) unfolding by a denaturing agent followed by returning it back to the “native” conditions. This discovery was further confirmed for many other proteins that were not subject to substantial posttranslational modification [2, 3].

In a living cell, a protein is synthesized on a ribosome and “matures under the care” of special protein-chaperones. Synthesis of a protein chain occurs during seconds to minutes. Overall production of the “complete” folded protein requires approximately the same period of time – there is no difference in the experiment [2-4].

Thus, one might suggest that protein folding starts on the ribosome even before completion of the synthesis of the protein chain. Apparently, this is the case for large multidomain proteins. Thus, luciferase (approximately 540 a.a.-long and folded into at least two domains) is active immediately after biosynthesis [4]. Apparently, folding of such a large protein in vitro can occur during a biologically-reasonable time interval, i.e. minutes (see Figs. 5 and 9 below), only in the case of “domain-by-domain” formation of its structure, which can be facilitated by the stepwise appearance of a protein chain from the ribosome. It is also known that the relatively small (about 150 a.a.) globin chain is already able to bind its ligand (heme) when the ribosome has only synthesized a little more than half of it [5]. These and similar facts lead to the assumption that cotranslational (and chaperone-dependent) folding of a protein chain in vivo significantly differs from its folding in vitro.

However, there is no noticeable difference between cotranslational in vivo folding and in vitro renaturation in the case of small single-domain proteins. According to some recent works [6-8], in the case of such proteins (which being labeled by ¹⁵N and ¹³C isotopes can be distinguished from the background of ribosomes and other cellular machinery) “polypeptides [on ribosomes] remain unstructured during elongation but fold into a compact, native-like structure when the entire sequence is available” [6, 7], and “cotranslational folding … proceeds through a compact, non-native conformation [i.e. apparently, through something like a molten globule – AF], …the compact state rearranges into a native-like structure immediately after the full domain sequence has emerged from the ribosome” [8]. Thus, in vivo, on the ribosome, an incomplete single-domain protein chain behaves as a shortened by several C-terminal amino acid residues in vitro: it does not form a certain spatial structure [9].

Two conclusions may be drawn from cotranslational behavior of small proteins.

First, it (similarly to behavior of the heme-binding N-terminal half of the globin chain, see above) is reminiscent of the behavior of “natively unfolded” proteins [10, 11], the majority of which represent molten globules and acquire certain spatial structure only upon binding a ligand.

Second, both in vivo and in vitro native structures emerge only in complete amino acid protein sequences (or in protein domains whose chains are usually sufficient for formation of their proper structures [12]).

Lack of a principal difference in folding is also true for participation of chaperones (whose main function is prevention of protein aggregation in the dense “cellular soup” [13]). Discovery of chaperones suggested that they possessed “structure-forming” catalytic activity (see, for instance, [14] and references therein); thus, formation of protein structure might proceed in completely different ways in vivo and in vitro. However, analysis of data provided in the work [14] showed that the best-studied chaperone, GroEL, does not accelerate protein folding [15]; these data rather confirm the previous conclusion [16, 17], that GroEL acts as a temporary “trap”, which binds folding protein chains present in abundance, thus preventing their irreversible aggregation.

Therefore, Anfinsen’s discovery of spontaneous folding in vitro [1, 18] (further confirmed for a number of other proteins), lack of cotranslational formation of native structures in incomplete proteins [6-8] along with the possibility of chemical synthesis of a polypeptide chain, which spontaneously folds into an active protein (experiments of Merrifield et al. [19]), – all this allows, to a first approximation, separating the spontaneous structure formation of a protein (at least, for a single-domain one) from its biosynthesis.

The present review focuses on exactly the spontaneous formation of a structure of a single-domain globular protein, i.e. on its in vitro folding.

HISTORICAL EXCURSUS

The ability of a protein chain to spontaneously fold into a complex spatial structure has been puzzling researchers for a long time: the chain must find its native structure (and the most stable one, as this structure is found both in vitro and during biogenesis, i.e. starting from various initial conditions) among a countless number of others during several minutes or seconds that are allocated by biology.

The number is truly great [20, 21]: at least 2¹⁰⁰ structures, but it is rather 3¹⁰⁰ or 10¹⁰⁰ or even 100¹⁰⁰ for a chain of 100 residues, as each residue can adopt at least two (“correct” and “wrong”), but rather even three (α, β, “coil”) or 10 [22] or even (10_by_φ) × (10_by_ψ) = 100 conformations [21]; thus, their “brute force” search should take about ~2¹⁰⁰, or 3¹⁰⁰, or 10¹⁰⁰, or 100¹⁰⁰ ps assuming that transition between conformations requires about 1 ps (the period of a thermal oscillation); this corresponds to ~10¹⁰, or 10²⁵, or 10⁸⁰, or even 10¹⁸⁰ years. A full search can only be “brute force” because a protein may “sense” conformation stability only by directly adopting it, as 1 Å deviation can greatly increase the chain energy in a dense protein globule.

Structural biologists and biophysicists were deeply influenced by “Levinthal’s paradox” (E. Shakhnovich compared this with the effect of “Fermat’s Last Theorem” on beginning mathematicians). Furthermore, under the influence of the hypothesis that cotranslational (and chaperone-dependent) in vivo folding of a protein chain significantly differs from its in vitro folding, many people assumed that there must be two solutions to this paradox: (i) for in vitro and (ii) for in vivo folding; and, probably, one more solution for folding of model protein chains in silico [B. K. Lee, remark on a seminar at NIH]!

Trying to solve his paradox, Levinthal suggested that a native protein structure is not determined by stability, i.e. not by the thermodynamics, but by the kinetics. Therefore, a protein follows some special “fast” folding pathway, and its native fold is just the end of this pathway with no regard for whether it is the most stable one. In other words, Levinthal assumed that native structure corresponds to a rapidly reachable minimum of chain free energy rather than the global one.

However, computer experiments with lattice protein models have convincingly demonstrated that chains folds into their most stable structure, i.e. the “native structure of a protein model” has the lowest energy, and thus protein folding is under thermodynamic rather than kinetic control [23, 24].

Nevertheless, most protein folding hypotheses are based on the “kinetic control hypothesis”.

In 1966 (even prior to Levinthal), Phillips suggested [25] that the protein folding core is formed at the N-terminus of its growing chain, whereas the remaining part is wrapped over this core. However, it was later demonstrated that successful in vitro folding of many single-domain proteins and protein domains does not commence at their N-termini [26, 27].

From personal memories. The paper of Phillips in Scientific American attracted my attention in the Moscow Lenin Library in the same 1966. After seeing there for the first time a picture of three-dimensional atomic protein structure, being a third-year student of PhysTech (the Moscow Institute of Physics and Technology), I said to myself: “I shall never have to deal with this nightmare”, and I was wrong…

Several years later, Wetlaufer [28] advanced the hypothesis that the folding core consists of residues situated close to each other in the chain. However, further in vitro experiments showed that this was not always the case [29].

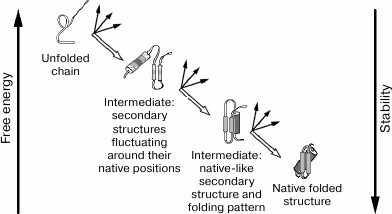
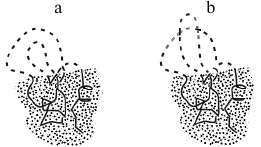
At the same time, Ptitsyn [30] proposed a model for hierarchic folding (Fig. 1) with stepwise involvement of various interactions and formation of diverse intermediate states.

According to this model, protein folding proceeds through several stages. In each of them, the most stable (for this stage) molecule shape is formed, which serves as an initial point for further stages of protein folding. In the example shown in Fig. 1, the choice of one native final structure out of ~2¹⁰⁰ possible structures, is reduced to three stages. At each of these stages, one structure is selected out of “only” ~2^100/3 possible structures, i.e. in the case of the stepwise mechanism selection of the final structure occurs ~2¹⁰⁰/(3 × 2^100/3) ~ 10²⁰ (!)-fold faster than in case of the brute force search.

Fig. 1. Ptitsyn’s stepwise model [30]. Secondary structures are shown – α-helices (cylinders), and β-regions (arrows). Both predicted intermediates were further found experimentally and referred to as: first – “pre-molten globule”, second – “molten globule” [31].

It should be noted, however, that this huge acceleration is reached due to irreversibility of choice of the optimal intermediate at each stage, and, therefore, a strong (by many k_BT, where k_B is the Boltzmann constant, and T is temperature) decrease in free energy at each stage. That is why rapid protein folding suggested by Ptitsyn can occur only if the native state of a protein is incomparably (by many-many k_BT) more stable than its unfolded state. At the same time, such “necessary superstability” of the protein’s native structure fundamentally contradicts the thermodynamics of phase transitions in protein molecules resolved by Privalov [22].

From personal memories. I remember very well heated debates between Ptitsyn and Privalov about the existence of protein folding intermediates and their thermodynamic and kinetic roles. Now, years later, it is clear that the folding intermediates discovered by Ptitsyn with the tip of his pen in 1973 and denied by Privalov exist in reality. They have been observed in many proteins both in kinetic and thermodynamic experiments [31, 32]. However, Ptitsyn’s main hypothesis about the necessity of existence of stable intermediates for protein folding was not confirmed. In many small proteins, stable folding intermediates are not observed at all [33], whereas in large proteins they are typically observed when the native state is much more stable than the denatured state, i.e. far from the point of thermodynamic equilibrium of these two states (under which protein folding also occurs, though significantly slower) [33-35]. Therefore, the two debaters were absolutely right about one point and wrong about another …

Closer to the end of this review I will consider Ptitsyn’s model in more detail, and we will see that based on this model, but with somewhat different interpretation, we can understand the reason for the rapidity of protein folding.

Finalizing discussion of the proposed approaches to solution of the protein folding issue, it should be mentioned that starting in the 1990s “folding funnels” became popular models for illustration and explanation of rapidity of protein folding [36-39]. However, they did not allow estimating – even approximately – time periods required for spontaneous folding of proteins. According to experiment (see below), for single-domain globular proteins these periods range from microseconds to hours.

Generally, complexity of the protein folding problem, considering a virtually infinite number of their possible structures, consists of the fact that it cannot be solved purely experimentally. Indeed, let us suppose that a protein chain possesses another “nonnative” kinetically very slowly reachable, but even more stable fold. How to find it, if the protein cannot find it itself? Should we wait for the result during 10¹⁰ (or even 10¹⁸⁰) years?

On the other hand, the question of whether kinetics or thermodynamics determines protein folding always rises in solving various applied tasks. It rises during sequence-based prediction of a protein structure (one must know what to predict: the most stable structure or the most rapidly folding one). It rises also in the case of designing new, not present in nature, proteins (one must know what to do: to maximally increase stability of desirable structure or to pave the fastest pathway to it).

However, is there indeed a contradiction between “stable” structure and the “fast folding” one? Maybe a stable structure is automatically the aim of “fast” pathways and thus automatically features fast folding?

Before addressing these questions, i.e. before considering the kinetic aspects of protein folding, let us remember several already well-studied fundamental facts from the field of thermodynamics (herein we always discuss relatively small single-domain proteins, 50-200 a.a. in length). These facts will facilitate our understanding of what folding process conditions we should consider. The thermodynamics facts are as follows.

1. The denatured form of proteins, at least of small proteins, unfolded with a strong and concentrated denaturing agent is often a coil [40].

2. Protein unfolding is reversible [18]. Furthermore, there may be equilibrium between denatured and native states [41], and transition between these states is an “all-or-none” process [22]. The latter means that at the protein denaturation point only two forms of the protein molecule are present at appreciable amounts: “native” and “denatured” ones, whereas all others (“semi-folded” and “misfolded” forms) are virtually absent. Such a transition is only possible for chains whose amino acid sequence provides sufficient “energy gap” between the majority of structures and the most stable of them [22, 42-45]; this provides reliability of protein functioning based on the “all-or-none” principle: as in a light bulb, it is either fully functional or completely not.

3. Under normal physiological conditions, the native form of a protein is only marginally (by several kcal/mol [22]) more stable than its denatured form (of course in a transition midpoint both these forms have the same stability); hence, the native form of a protein is stable due to its low energy, whereas the unfolded one is stable due to its high conformational entropy, i.e. due to vast number of various unfolded conformations.

Necessary clarification: as accepted in the literature, the term “energy” implies here, strictly speaking, all free energy of interactions including chain-solvent interactions (for instance, “energy” of hydrophobic interactions is determined by solvent entropy [40]). The term “entropy” comprises here only the chain conformational entropy, but not the solvent entropy. Such terminology is adopted to leave the solvent out and to focus on the main problem – how the protein chain finds “its” spatial structure among the vast number of possible ones.

The above-mentioned “all-or-none” transition means that the native (N) and the unfolded (U) states are separated with a high free-energy barrier.

It is height of this barrier that limits the rate of the transition, and this height should be estimated to solve Levinthal’s paradox.

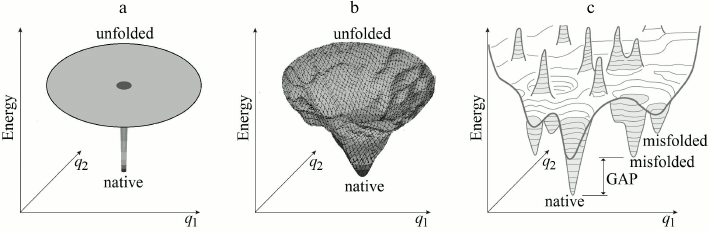
For the beginning, however, it is appropriate to determine whether “Levinthal’s paradox” is indeed a paradox? Already Bryngelson and Wolynes [46] noted that this “paradox” is based on an absolutely flat (and therefore nonrealistic) “golf course” model for describing a protein’s potential energy surface (Fig. 2a).

Fig. 2. Main models of energy landscapes of protein chain: Levinthal’s “golf course” (a) and the “funnel” of Leopold et al. (b); both possess the lowest energy (“native”) structure in the middle. c) More realistic picture of a bumpy energy landscape of the protein chain. Broad (of many k_BT_melt, where k_B is the Boltzmann’s constant, T_melt is a protein melting temperature) energy gap between the global energy minimum and other energy minima is required for providing the “all-or-none” transition upon destruction of stable protein structure [22, 42, 43]. Only two coordinates (q₁ and q₂) can be depicted on the figure, whereas the chain conformation is determined by hundreds of coordinates.

Somewhat later, Leopold et al. [36], following ideas of Go and Abe [47], considered a more realistic energy surface model (with inclination toward native protein structure) and introduced “folding funnels” (Fig. 2b), which seemed to eliminate “Levinthal’s paradox”.

However, not everything is so simple…

The problem of the huge time required for a search for the most stable structure does exist: it was proved mathematically that despite funnels, etc., a search for such structure is a so-called “NP-hard problem” [48, 49], which roughly speaking requires a huge (exponentially-large) time for its solution (by both a folding chain and a human).

Anyway, various “funnel” models became a popular way to explain and depict protein folding [37, 50, 51]. The lowest energy structure (which is formed by the most powerful chain interactions) situated at the middle of the funnel is surrounded by higher energy structures, which only comprise some of these interactions. An “energy funnel” directs the shift toward the lowest energy structure, which apparently should help the protein to avoid “Levinthal’s brute force search”.

Nevertheless, it is possible to demonstrate that energy funnels as such do not resolve Levinthal’s paradox. Analysis [52] of strictly formulated funnel models [39, 53] shows that at the equilibrium between folded and unfolded chain forms, these models are unable to explain simultaneously both main features observed during protein folding: (i) non-astronomical folding time, and (ii) “all-or-none” transition, i.e. coexistence of native and unfolded forms of protein molecules during folding.

Besides, as mentioned above, the stepwise mechanism of protein folding [30] as such is also unable to [54] explain simultaneously both these main features observed during protein folding.

Hence, neither the stepwise mechanism nor “funnels” can resolve Levinthal’s problem, though they suggest what may accelerate protein folding.

A fundamental solution of the paradox is provided by a special funnel type, considering separation of unfolded and native phases in a folding chain [55, 56] (see also review [57]).

The next part of our review is devoted to this solution.

PHYSICAL THEORIES AND THEIR RESULTS

Physical estimation of free-energy barrier height separating native and unfolded chain states: A view of the barrier from the native-state side. To resolve “Levinthal’s paradox” and to demonstrate that the most stable protein chain structure may (or may not?) be found during a reasonable time, we may to a first approximation consider only rate of “all-or-none” transition from the coil to the most stable chain structure. At the same time, it is sufficient to consider the case when the most stable chain fold is as stable as the coil (or only marginally more stable than it), whereas all other forms of a protein chain are thermodynamically unstable. Here, observing the protein folding is the easiest, as there are no stable folding intermediates: they only appear when the native structure becomes much more stable than coil; then the fastest protein folding occurs [33], but analyzing it becomes more difficult. Therefore, we will first focus on the point of equilibrium between the native structure and the coil, where protein folding is not the fastest, but the simplest.

From personal memories. I remember well that during discussing the protein folding problem in 1970s, 80s and even 90s, almost all of us one way or another were focused on the environmental conditions in which the process proceeded at the fastest rate (it was accepted that this would emulate “physiological” intracellular conditions); see for instance [30, 31, 33, 58]. Such attention to the “physiological” conditions was reasonable from the biological point of view. However, the main physical question – how the protein manages to find its structure during a non-astronomical time period – was shaded by a number of secondary (as much as I understand now) for answering this question details; for instance a question about the destiny of metastable folding intermediates (which simply does not exist when protein folding is examined near the point of thermodynamic equilibrium between the native structure and the coil), and all attention must be focused on the transition state [33]. I may not leave unnoted the fact that intense attention to this equilibrium point differentiates the approach, which we develop now, from those that were prevailing from the 1960s to the 1990s.

As an “all-or-none” transition requires a broad energy gap between the most stable structure and others [22, 42-45] (Fig. 2c), we will assume that an amino acid sequence under study provides such a gap. Our aim is to estimate rapidity of the “all-or-none” transition and to prove (if possible) that the most stable structure of a protein or a normal size domain (~100 a.a. in size) may emerge within several seconds or minutes.

To prove that the most stable structure should fold rapidly, it is sufficient to demonstrate that this structure can always be formed through at least one “fast” folding pathway. Existence of many reaction pathways would only accelerate the process…

At the same time, we may avoid considering pathways leading to formation of non-native structures (therefore, in the presence of the “gap” – high energy ones)! They cannot “destroy the true pass” for our chain. Indeed, near the “all-or-none” mid-transition between the most stable structure and the coil, no “semi-folded” or “misfolded” states can serve as traps – they cannot “absorb” folding chains just because their total stability is small. A good analogy here would be water leakage through cracks in a wall separating two swimming pools: if “capacitance” of the cracks is small, i.e. they cannot absorb all the water, any new crack may only accelerate filling of the second pool. Thus, examining leakage through a single crack, we estimate a minimal filling rate.

To provide fast folding, any step of the pathway should be fast, the number of steps should not be large, and – the main thing! – the folding pathway must not contain very high energy “barriers” at any stage.

As interval of time required for fixation of one link is small (nanoseconds, judging by measured growth rate of α-helices in polypeptide chains [59]), a protein fixing its links one-by-one would fold instantly (100-link chain in less than ~1000 ns) in the case when it would not have to overcome a free-energy barrier. Protein folding takes several seconds or minutes rather than microseconds because of the free-energy barrier: most of the time span is spent for ascending to this barrier and falling back, but not for movement along the folding pathway.

The “transition state” (i.e. the least stable “barrier state” in the reaction pathway) plays a key role in this process. According to a classical transition-state theory [60-62], time of the process of crossing the barrier is calculated as:

TIME ~ τ × exp(+ΔF^#/k_BT), (1)

where τ is the characteristic time of a single step of the process (normally about a nanosecond), ΔF^# is the height of the free-energy barrier.

As to ΔF^#, the main question to be answered is whether the ΔF^# barrier in the pathway leading to the most stable state of a protein chain is high.

Folding of a protein chain leads to decrease in both its entropy (because its ordering grows) and energy (due to formation of contacts between approaching chain links). Energy decrease reduces whereas entropy decrease elevates the chain free energy.

If during folding the chain must closely approach its final structure before emergence of the contacts, which should stabilize this structure (i.e. the chain must loose almost all its energy before it starts gaining energy), the increase in the free energy at the first folding stage will be proportional to the number of links in the chain, i.e. it will be very high, and the chain folding will be very slow. This is exactly the idea (losing all entropy before gaining energy) underlying Levinthal’s paradox, which claims that a protein chain cannot find its most stable structure even during the lifespan of the universe.

On the contrary, if during folding, reduction of entropy is immediately compensated by reduction of energy [47], then this pathway is not blocked by a high free-energy barrier, and folding passes quite fast. Exactly this picture exists, as I will show.

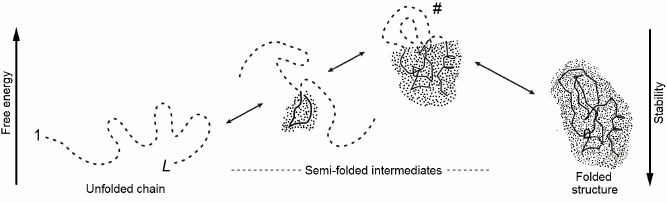
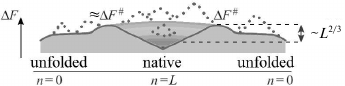
Let us consider change of energy ΔE, entropy ΔS, and resulting free energy ΔF = ΔE – TΔS during sequential protein folding (or as they say, folding according to a nucleation [26] mechanism) depicted in Fig. 3. At every step of this pathway, one link is extracted from the coil and adopts the position corresponding to the final (the most stable) structure of the globule.

Fig. 3. One possible pathway of sequential protein folding with separation of unfolded and globular phases [56]. The free energy of folding intermediates is increased due to their phase interface. Symbol # indicates maximally unstable (transition) state. The dotted area corresponds to the protein part that already acquired its final conformation; the protein main chain is indicated by a solid line, whereas the side chains are omitted to simplify the figure. The dashed line indicates still unfolded chain. The globular moiety of “semi-folded” structures lying at the “optimal” (passing through intermediates with low free energy) pathway should be compact, i.e. possessing the minimal interface between the folded and the unfolded phases.

Such a process may seem somewhat artificial (how can a link know its position in a final structure?). However, this impression disappears when one notes that this way we just watch “the movie” of decomposition of the stable structure of the protein backwards and remembers that, in accordance with the well-known in physics principle of detailed balance [63], direct and reverse reactions pass through the same pathway and feature the same rate when both states possess equal stabilities.

Therefore, one may utilize the principle of detailed balance to find the folding transit state by finding the optimal unfolding transit state. Analysis of an unfolding pathway as advantageous as it is much simpler: for any globular structure, one can easily find a pathway for sequential unfolding passing through the least unstable, i.e. characterized by the minimal interface between globular and “unfolded” phases, compact semi-unfolded states (Fig. 3) [55, 56, 64-66].

From personal memories:

1) As much as I remember, protein unfolding, in contrast to folding, was never considered to be “paradoxical”, though it was for a long time well known that the native state can occur in a kinetic equilibrium with the unfolded one. In my opinion, no one ever asks a question in addition to Levinthal’s paradox – how, again, a protein can during “non-astronomical” time period obtain such a great amount of energy required for its unfolding… The absence of such question demonstrates how much easier it is to imagine unfolding of any protein structure rather than its folding…

2) We first faced the phase-separation problem when searched for reasons of the “all-or-none” phase transition upon protein melting [67]. However, at that time we have not guessed to study the influence of this effect not only on the phase character, but also on kinetics of this transition – otherwise Levinthal’s paradox should have been resolved 15 years earlier.

Considering the pathway of sequential folding (reconstructed from the sequential unfolding pathway), we see that, along with growth of the final globule, interactions stabilizing the final structure are restored in it one-by-one.

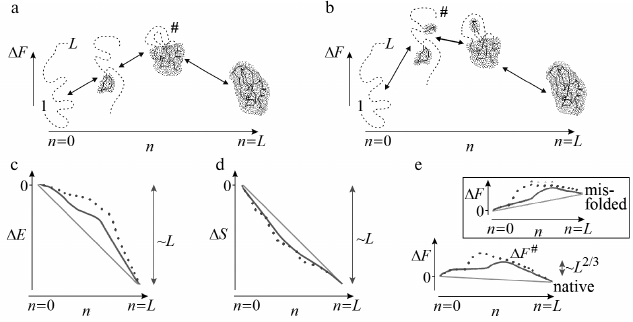
If a growing structure always stays rather compact, as it is in Figs. 3 and 4a (optimal pathways of exactly this type should be of interest for us), then the number of these interactions will grow (whereas their energy will decrease) almost proportionally to n fixed links in a globule (Fig. 4c).

Fig. 4. Sequential folding/unfolding with compact (a) and noncompact (b) intermediates, and changes in energy (c), entropy (d), and free energy (e) along these pathways near the thermodynamic equilibrium between the coil (n = 0) and the final structure (n = L: all L links are packed in a globule). Full change of energy, ΔE(L), and entropy, ΔS(L), are approximately proportional to L. Bold lines in panels (c) and (d) indicate linear (proportional to n already packed links) portions of ΔE(n) and ΔS(n). Nonlinear portions of ΔE(n) and ΔS(n) are determined mainly by the surface of the globular moiety of the molecule (solid lines – for pathway with compact intermediates; dashed lines – for pathway with noncompact ones). Maximal ΔE(n) and ΔS(n) deviations from linear dependences are proportional to L^2/3. As a result, ΔF(n) = ΔE(n) – TΔS(n) also deviates from linear dependence (bold straight line) by ~L^2/3 in the case of compact intermediates (and more than that in the case of noncompact ones). Thus, at the equilibrium point (where ΔF(n = 0) = ΔF(L)), maximum excess (“barrier”) ΔF^# in the pathway with compact intermediates is also proportional to just L^2/3. Change in ΔF(n) in the pathway toward other structures looks approximately the same (see inset in panel (e)), but these pathways can be neglected as all these structures are unstable, i.e., have ΔF(n = 0) < ΔF(L) in the presence of the energy gap between the most stable and other globules and “all-or-none” transition between the unfolded and the most stable globular state. Taken from [56].

In reality, at the beginning of folding decrease in energy is somewhat slowed as attachment of a link to a surface of a small globule provides generally smaller number of contacts than attachment to a surface of a large one. As a result, a nonlinear (i.e. proportional to ~n^2/3) surface term emerges in energy ΔE for a growing globule. For this reason, maximum deviation from linear energy decrease is ~L^2/3 (where L is a number of links in a chain) in the pathway passing through compact intermediates (Fig. 4a) [55, 56, 65] (and more if intermediates are not compact; Fig. 4b). This deviation is apparently small compared to full energy decrease upon the chain folding, whose value is proportional to L.

Along with growth of a globule, entropy of a chain is also decreased approximately proportionally to number of links incorporated into the globule (Fig. 4d). Though, in the beginning of the folding entropy may drop somewhat faster due to formation of closed loops protruding from a growing globule (Figs. 3, 4a, and 4b).

Consequently, a nonlinear (surface) term emerges in entropy ΔS of this growing globule, which is (similarly to that in ΔE) about L^2/3 [55, 56]. More precisely, ~L^2/3ln(L^1/3), as an unfolded loop protruding from the surface of a semi-folded globule is ~L^1/3 long and the entropy of the loop of this size is ~ln(L^1/3) [68, 69], while ln(L^1/3) ~ 1 if L ~ 100; for more precise estimation see below, after Eq. (3). This decrease (see [55, 56] and more recent purely mathematic works [70, 71]) is significantly lower than the decrease in entropy as such, which is (similarly to the energy decrease) proportional to L.

Both linear and surface terms of ΔS and ΔE are included in the free energy ΔF = ΔE – TΔS of a growing (or unfolding) globule. When the accomplished globule is at equilibrium with the coil, the larger linear terms mutually annihilate in the difference ΔE – TΔS (as ΔF(n = 0) = ΔF(L)), and only surface terms remain: without them, ΔF(n) should be equal to zero for the whole pathway.

Therefore, the free-energy barrier (see Fig. 4e) in the pathway of sequential folding with compact intermediates is only determined by relatively small effects related to the surface of the globular intermediates, and its height is proportional not to L (as it is suggested Levinthal’s estimation), but only to L^2/3.

In a simplified form (see detailed calculations in [55, 56, 65, 72]), the free energy of the barrier is estimated as follows.

The fastest folding pathway is the one featuring the lowest free-energy barrier. In any given pathway, the barrier corresponds to an intermediate with the highest free energy, i.e. to the one having maximal in this pathway interface of folded and unfolded phases. In the case of compact intermediates, such an interface contains about L^2/3 residues. The energy term ΔE^# of the free energy of the barrier emerges due to interactions lost by the residues situated at the interface; it is approximately equal to:

L^2/3·¹/₄·ε, (2)

where ε ≈ 1.3 kcal/mol ≈ 2k_BT_melt is a mean melting heat of an amino acid residue in a protein [22] (this is the first empirical parameter utilized in the theory), and ≈1/4 is the portion of interactions lost by the residue at the interface on average. Thus,

ΔE^#//k_BT_melt ≈ 0.5 L^2/3. (2a)

The entropic term ΔS^# of the free energy of the barrier is related to loss of entropy by closed loops protruding from the globular phase to the unfolded phase (see Figs. 3, 4a, and 4b).

The upper limit for ΔS^# is zero (if there are no such loops at the interface).

The lower limit for ΔS^# is about

(ΔS^#)_lower = ¹/₆·L^2/3·[–⁵/₂·k_B·ln(3·L^1/3)], (3)

where ¹/₆·L^2/3as a maximum number of closed loops at the optimal (with lowest number of loops) globule/coil interface. In reality, this is a mean value for one cross-section of a globule (Figs. 3 and 4a), as the residue at the interface may have six directions (four along with the surface, one – inward, and just one – outward), while an interface utilized in folding must be covered by minimal, i.e. not more than this mean, number of loops. 3·L^1/3≡ (L/2)/(¹/₆·L^2/3) is the mean number of residues in such a loop (it is equal to number of unfolded residues divided by number of loops), and –⁵/₂·k_B·ln(3·L^1/3) is the entropy lost by such closed loop (whose inner parts do not penetrate inside the globule, which changes conventional Flory coefficient from ³/₂to ⁵/₂ [55, 56]). If L ~ 100 (this approximation is apparently adequate for the entire range of L = 10-1000),

(ΔS^#)_lower ≈ –k_B·L^2/3. (3a)

As a result, time of both formation and unfolding of the most stable structure growth along with number of residues in a chain L not “according to Levinthal” (i.e. not as 2^L or 10^L or any number raised to the power of L), but, at the middle of the transition, as:

TIME ~ τ × exp[(1 ± 0.5)L^2/3], (4)

where τ ≈ 10 ns [59] (this is the second and the last empirical parameter utilized in the theory).

Time estimated in this way depends on both size and shape (which determines by means of ΔS^# factor 1 ± 0.5; see above) of the protein’s native structure.

The physical reasons for this “non-Levinthal” estimate are as follows: (i) decrease in entropy upon folding is almost immediately and almost completely compensated by energy decrease during sequential folding (and similarly energy increase is almost immediately and almost completely compensated by the increase in entropy during the same sequential unfolding pathway); (ii) the free energy of the barrier emerges because of increase in free energy related only to surface effects, which are relatively weak.

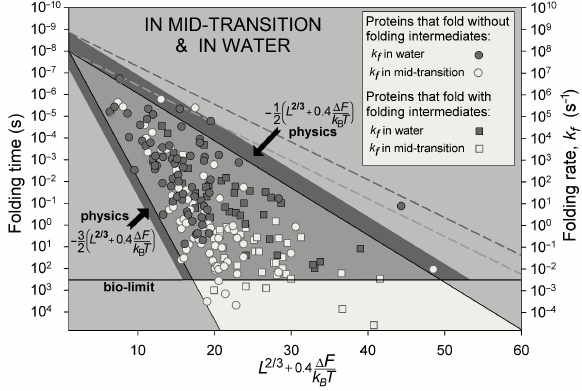
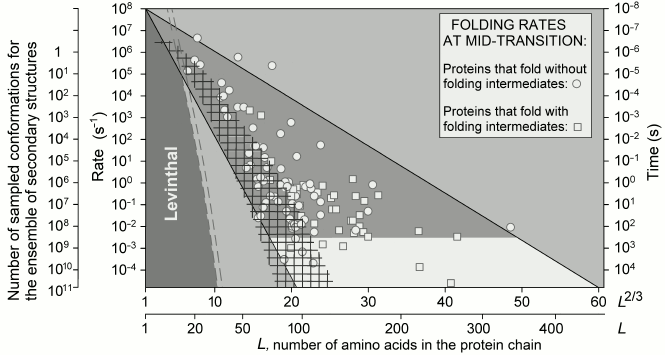
The observed time periods required for protein folding (Fig. 5) cover about 11 orders of magnitude (this is comparable with a difference between the lifespan of a mosquito and the age of the Universe).

At the middle of the transition (at ΔF = 0), these time periods are indeed (Fig. 5) within the theoretically outlined limits {10 ns × exp(0.5L^2/3) – 10 ns × exp(1.5L^2/3)}. Under more “physiological” conditions (“in water”, where ΔF < 0), L^2/3 is changed to L^2/3+ 0.4ΔF/k_BT [65] (see discussion), but in all other respects the range stays the same.

Fig. 5. Experimentally measured in vitro protein folding rate constants in water (under approximately “biological” conditions) and at the middle of the transition (in the presence of small quantities of a denaturing agent) for 107 singe-domain globular proteins (or isolated domains) without S–S bonds and covalently attached ligands (though, S–S bonds do not significantly affect rate of protein folding [73]). Triangle: physically allowed area; light gray (with a darker band) corresponds to biologically reasonable folding time (≤10 min); larger time periods (i.e. lower rates) required for folding are observed (for some proteins) only at the middle of the transition, i.e. under nonbiological conditions. Light dashed line limits area of rates for oblate (1 : 2) and oblong (2 : 1) globules at the middle of the transition; darker dashed line – under “biologically-relevant” conditions. L is number of amino acid residues in the protein chain; ΔF ≤ 0 is difference of free energy between the native and the unfolded states of a chain. Taken from [65].

The formula obtained (4) and Fig. 5 demonstrate that a chain of L ≲ 80-90 residues should always find its most stable structure during minutes even under “nonbiological” conditions at the middle of the transition, where, as it is known [33, 41], folding proceeds at the lowest rate. This means that structures of such small proteins are under thermodynamic control: they are the most stable among all structures of such chains. The native structures of larger proteins (of 90-400 residues) are under additional “structural” control in the sense that the most “tangled” folds of such long chains may not be reached during days or weeks even if they are thermodynamically stable; indeed, highly “tangled” folds are never observed in long protein chains [65] – they are apparently excluded from the diversity of protein structures. It also explains why large proteins should be either nonspherical, or consist of several domains: otherwise chains over 400 residues long would fold inappropriately slowly to function in a cell. This is the “structural” control, whose action is similar to that of Levinthal’s “kinetic control”, though at another level and only for large proteins. The estimates above (80-90 and ≈400 residues) will somewhat increase if free energy ΔF of the native structure is lower than that of the unfolded chain (see below), but remain essentially the same [65].

One more thing to mention. “Quasi-Levinthal” brute force search for correct knot formation (Fig. 6) may actually limit folding rate, as a knot cannot be changed without decomposition of a globular portion. However, computer simulations demonstrate that one knot includes about 100 residues (see references in [72]); thus, the search for a correct knotting can limit only very large chains [72], which anyway cannot be folded within a reasonable interval of time (according to Eq. (4)).

Fig. 6. a) A compact folding intermediate with protruding unfolded loops. Growth of the intermediate corresponds to a shift of border between fixed (globular) and unfolded (coil) portions of the protein chain. Successful folding of the intermediate requires proper formation of knots in its chain: semi-folded structure with wrong knotting (b) is unable to grow to properly folded protein, it should first unfold. However, a ~100-link-long chain can only contain one or two knots, so the search among intermediates with different loop knotting should not limit the protein folding rate [72].

Estimating dependence of extent of search in conformational space for native protein structure on its size: A view of the barrier from the unfolded state side. The above estimate for the protein folding time is actually based on analysis its unfolding, and not folding, because for any structure it is easier to define a good unfolding pathway (and to estimate time required for that, see above) than a good pathway leading to folding of a structure with the least energy, whereas the free-energy barrier is the same for both pathways.

In other words, we considered free-energy barrier between folded and unfolded states (Fig. 4e), focusing on the side corresponding to energy increase along the way from the volcano conduit to the crater edge (Fig. 7; compare with Fig. 4e), and we did not yet consider the barrier side, which is associated with loss of entropy along the way from unfolded state to the crater edge.

Fig. 7. This purely illustrative figure demonstrates how entropy converts an energy funnel (depicted in Fig. 2b) into a “volcano-like”, as it is called now [74], landscape of free energy with free-energy barriers (see Fig. 4e) in each pathway from unfolded state to a globular state. Any pathway from unfolded state to a globular one first ascends a barrier, i.e. the edge of the volcanic crater, and only then begins descending to the “funnel”, i.e. into the crater. Smooth free-energy landscape corresponds to compact semi-folded intermediate structures (depicted in Fig. 4a), whereas “rocks” (outlined with dashed lines) represent a landscape that also includes noncompact semi-folded intermediates (shown in Fig. 4b). A more correct though less elegant scheme of free-energy landscape is provided in Fig. 2 in the report [64].

As rates of direct and reverse reactions are equal at the middle of a transition (as follows from the physical principle of “detailed balance”), both sides of the barrier are of the same height, and thus considering just one side (“unfolding side”) is sufficient for estimating the barrier height.

However, to complete the analysis, one must consider the other side of the barrier – the one that is the most interesting for biologists: it is associated with the folding (i.e. with loss of entropy). Doing this we will observe the protein-folding puzzle from a different angle.

To dissect folding, a search for a stable conformation of the protein chain should be made.

The full conformational space for a chain estimated by Levinthal [21] at the amino acid residue level is truly huge: from 3¹⁰⁰ to 100¹⁰⁰ conformations for a chain of 100 residues.

However, should the chain try all these 100¹⁰⁰ conformations in a search of the most stable of them? No, conformational space is covered by local energy minima; each of these is surrounded with a local energy funnel providing rapid descending to this minimum (see Fig. 2b and [75], and Fig. 6 in [76] in this issue of Biochemistry (Moscow)). Thus, during a search for the global energy minimum, the enormous Levinthal’s brute force search for mainly noncompact chain conformations can be substituted by a much smaller search for compact globular structures corresponding to deep energy minima.

Therefore, to estimate the search space one must estimate the number of deep local energy minima (as well as time of transition from one minimum to another). In a certain sense, it is similar to a search for possible “topomers” of a protein chain [77, 78]. However, our goal now is not to calculate the protein folding rate: we only need to assess the lower limit of this rate, which is principally different from the search for topomers.

Browsing protein structures shows that interactions in them are mainly associated with secondary structures [79-81]. Thus, a question rises about how many energy minima exist at the level of formation and assembly of secondary structures into globule, i.e. at the level that was considered by Ptitsyn [30] in his stepwise protein-folding model.

This number appears to be lower by many orders of magnitude than the number of conformations of amino acid residues, i.e. 100^L or 10^L or 3^L, and it reaches ~L^N for an L-link chain having N elements of secondary structure [82]. The value of N is much smaller than of L, which is the reason for strong decrease in conformational space.

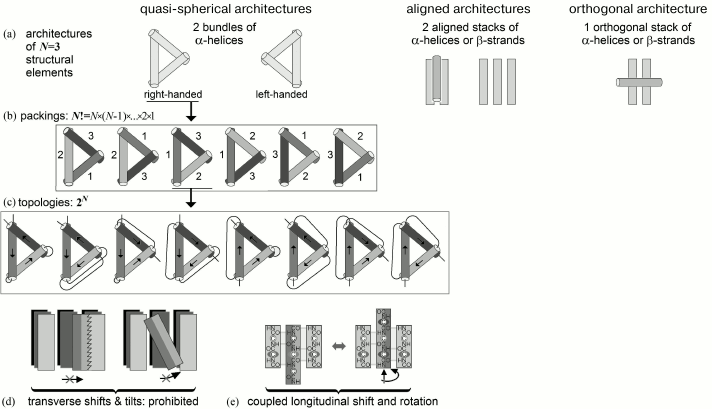
The order of L^N was assessed as follows (Fig. 8).

Fig. 8. Scheme for estimating conformational space at the level of all possible folds of structural elements. Taken from Appendix to [82].

Number of architectures (i.e. types of tight folds of secondary structures) is small (see [79, 80, 83]) – typically, ~10 or lower for a given set of secondary structures (Fig. 8a), because architectures are folds of secondary structure layers (each contains several structural elements), and therefore combinatorics of layers is very small compared to that of much more numerous elements of secondary structure (see below).

The maximal number of folds, i.e. all positional combinations for N elements, in a given protein architecture is N! ≡ N × (N – 1)×. . . ×2×1 (Fig. 8b).

The maximal number of topologies, i.e. all combinations of directions of these elements, cannot exceed 2^N (Fig. 8c).

Transverse shifts and tilts of an element inside a tight fold are prohibited (Fig. 8d).

Shifts and rotations of elements of a secondary structure within a dense fold are closely coupled (this is shown in Fig. 8e for β-sheet, where such connection is the most obvious, but it is also true for α-helices – let us remember Crick’s “knobs-into-holes” packing [84]). As a result, each α or β element may have approximately L/N (i.e. about the average length of an element) possible “shift-rotations” in a globule formed by N structural elements in an L-link chain.

All this limits number of energy minima in conformational space to ~10 × (L/N)^N× 2^N× N!; which (using Stirling’s approximation N! ~ (N/e)^N) gives in the main term at L >> N >> 1 [82]:

NUMBER of energy minima subject to searching ~ L^N. (5)

This number can be further reduced by symmetry of a globule; besides, α-helix cannot be placed into a β-sheet regardless of regrouping other elements, and vice versa, because β-strand requires a partner, another β-strand, to form hydrogen bonds, whereas α-helix avoids such partnership. Moreover, short or crossing loops between structural elements may not allow adopting random positions and directions within a globule, etc. [85]. However, this reduction is not important for us, because our goal is to assess upper limit of the number of configurations.

Here, a question arises: how does a chain know where and what secondary structure should be formed? The answer seems to be the following: the majority of secondary structures are determined by local amino acid sequences [30, 86, 87]. Anyway, the choice “to be or not to be” only adds just one state to the already considered number L/N of its possible shift-rotations, whereas α ↔ β transition just doubles it, which is not significant, see [88].

In a not too small compact globule, the length of a secondary structure element should be proportional to the diameter of the globule, i.e. ~L^1/3. More precisely: globule volume ≈150 Å³× L (and, therefore, its diameter ≈ 5 Å × L^1/3), whereas a shift by one residue is 1.5 Å in α-helix and ≈3 Å³ in an elongated chain [81]. Therefore, α-helix contains ≈3L^1/3 residues, while β-strand or loop consists of ≈1.5L^1/3 residues, i.e.

NUMBER of elements “secondary structure + loop” N ≈ L^2/3/4.5 — L^2/3/3, (6)

while expected L^N value (i.e. estimation of complete search volume) is within limits:

~L^{L^2/3/4.5} ≡ exp([ln(L)/4.5] × L^2/3]) — L^{L^2/3/3} ≡ exp([ln(L)/3] × L^2/3]). (7)

Analogous dependence of L^N value on L comes [70, 71] from strictly mathematical analysis of the degree of complexity of a search task.

As ln(L)/4.5 ≈ 1 and ln(L)/3 ≈ 1.5 at L ≈ 80-90, the above limits are close to the upper limit determined by Eq. (4).

On the other hand, L/N value (i.e. average number of residues per secondary structure element with an accompanying loop) is 15 ± 5 according protein statistics [74]; this also leads to L^N value that is very close to the above estimate.

Adopting from experiments on folding of the smallest proteins [89, 90] 1 µs as an estimate of the time required for “viewing” one configuration, and taking L/N = 15 ± 5 from protein statistics, we see that the time theoretically required for screening the entire conformational space during formation and packing of a secondary structure is approximately equal (Fig. 9) to the upper limit of experimental folding times observed for small (L ≲ 80-90 residues) proteins, whose structure selection is determined by stability, as we already know.

Fig. 9. Rate of search and rate of folding. Folding rates (circles and rectangles) are shown for proteins experimentally studied in vitro at the middle of their transition (i.e. at equal stabilities of their native and unfolded states); large light triangle – predicted (from analysis of unfolding!) range of these rates (compare with Fig. 5). Mesh shading – theoretical estimate of minimal rate of full search, during folding, for all possible packings of secondary structures (α-helices and β-strands). Limit of “Levinthal search rate” (10¹²s^–1/3^L at only three possible residue states: α, β, and coil) is shown with double-dashed line, whereas rates of such searches at 10 or 100 states of a residue are significantly lower (in the dark-gray zone on the left). The figure is taken from [91].

The above does not mean that a protein chain must check all its conformations at the level of formation and packaging of secondary structures (though a chain of 80-90 or fewer residues can do it within minutes, as shown for some proteins in Fig. 9). It only means that the “energy funnel” leading to the native structure starts working at the level of secondary structures, and thus should accelerate folding by only several orders of magnitude (as it is demonstrated in Fig. 9 for the majority of the proteins), but not by tens and hundreds of orders of magnitude, which should happen in case it should have to start working at the level of amino acid residues (compare with the topomer-sampling model by Debe et al. [77] and Makarov and Plaxco [78]). Figure 9 shows that the acceleration is especially notable for chains of >100 residues, but even in this case the main work is done by secondary structures.

From the bird’s eye view, the estimates (4)-(7) of the number of chain conformations subject to a search during finding its most stable conformation appears as follows. This number is determined, in the main term, by size of the globule’s surface – by number of surface residues, or, which is almost the same, by the number of secondary structures N (both these parameters are proportional to L^2/3). The physical reason is that all independent degrees of freedom in a dense globule are associated with its surface, since a dense globule prohibits independent regrouping of its residues [45, 92] – as well as a secondary structure does. From this point of view, secondary structures that we used here are not required for the fundamental estimates (let us note that similar estimates by Fu and Wanf [70] and Steinhofel et al. [71] and our previous estimates [55, 56, 64, 65, 93] did not utilize secondary structures), though these structures actually form the core of a protein globule and they are useful for clarification of the fundamental estimates obtained.

CONCLUSION

We have examined pathways of a folding protein chain through the “volcano-like” free-energy landscape depicted in Fig. 7 both from the volcano base to its crater and from the throat to the crater edge. Therefore, we studied both sides of the barrier separating folded and unfolded states of chain by a crossing the barrier forward and backward, and learned about two aspects of protein folding/unfolding that solve Levinthal’s paradox.

The side of the barrier facing the native structure is easier to analyze, because for any structure it is easier to outline a reasonable unfolding pathway than a folding pathway to a structure still unknown to the chain. Analysis of unfolding, i.e. the view from inside the folding funnel, allowed estimating the range of unfolding time periods; and further, the detailed balance principle revealed the range of folding (or, more precisely, searching) time periods. At the same time, analysis of the folding itself only revealed the upper limit of this range.

Let us note that the same scheme may be applied for formation of the native structure of a protein starting not only from a coil (which we used here for simplicity), but also from a molten globule or another state. But, for these processes (where, nevertheless, experiment does not demonstrate significant folding acceleration, see Figs. 5 and 9) all estimates were much more difficult because analyzing the denatured but not completely unfolded state is difficult. That is why we will not go beyond the simple case – formation of native structure from a coil.

We should notice that “Levinthal’s problem” also exists for crystallization (it is similar to protein folding – in this case different atoms also must choose one of numerous configurations in a “so far unknown” to them crystal); however, to our knowledge, it did not attract much attention there as compared to the case of proteins [94, 95].

Several concluding remarks:

1. Our estimate of the number of secondary structure ensembles subject to search (i.e. number of corresponding energy minima for a protein chain) does not depend on stability of these ensembles (Eqs. (5)-(7)). The effect of stability (ΔF) of the native state on folding time is considered below.

2. So far, our estimate (4) of the folding time was associated with the point of equilibrium between the unfolded and the native states, where ΔF = 0, whereas observed folding time is maximal, but it may exceed by orders of magnitude folding time under native conditions [33].

A question is appropriate: how does folding time change when the native state becomes more stable than the coil (i.e. at ΔF < 0)? Both experimental [33] and theoretical analysis [56] indicate that at small (but still, about several k_BT, so that stable intermediates do not form) –ΔF value, the folding time is reduced along with growing stability, and, in theory [65], it may be estimated as:

TIME ~ τ × exp[(1 ± 0.5) × (L^2/3 + 0.4 × ΔF/k_BT)], (8)

where 0.4 factor corresponds to theoretical estimate of the chain portion involved in the folding core. Thus, 0.4 × ΔF is an estimate of change of free energy of the core. This equation allows assessing rates of folding that occur under different conditions (Fig. 5).

For the case of very high stability of the native state (–ΔF >> k_BT), Thirumalai [96] proposed the rule ln(TIME) ~ L^1/2, which differs from Eq. (4), but is similar to it. In this case, fast protein folding passes “downhill” (energy-wise), but the “energy slope” has (because of protein heterogeneity) bumps with energy proportional to L^1/2. However, numerical experiments on protein lattice models have demonstrated [35, 58] that for the temperature providing the fastest folding, its time grows along with chain length as ln(TIME) ~ A × ln(L). Coefficient A there is equal to six for “random” chains and four for chains “edited” for the fastest folding and possessing large energy gap between the most stable fold and others. This again demonstrates dependence of folding rate on experimental conditions and size of energy gap [44, 57].

3. Some proteins are “metamorphic” [97]: they are observed in two different structures. We are most interested in a very few of them (for instance, serpin), which first acquire “native” structure functioning in a cell or in a tube for about an hour, and then convert to another, nonworking but more stable structure [98]. What is important is that this transition is not associated with a change in the protein’s environment (i.e. aggregation, as in the case of amyloids, or formation of any complexes). Therefore, a chain of such protein possesses two stable structures: first one folds faster, another one is more stable. Apparently, such proteins should be very rare: theoretical estimates [35, 81] suggest that an amino acid sequence encoding one stable structure (whose energy is separated by large energy gap from energy of others) is a rarity as such, whereas a sequence encoding two stable structures is a rarity squared…

4. Equations (4) and (8) assess the range of possible folding rates rather than folding rates for individual proteins, which can differ (Fig. 5) by several orders of magnitude even for proteins of the same size. The effect of folding pattern of a certain protein chain on folding time may be assessed using a phenomenological “contact order” parameter (CO%) [99]. CO% is equal to mean distance (by sequence) between residues contacting in a native protein divided by chain length (see also [51, 100]). Large CO% indicates presence of numerous closed loops in a native globule, whereas high value of coefficient (1 ± 0.5) in Eqs. (4) and (8) indicates their presence on the surface of a semi-folded globule (Fig. 6). Therefore CO% is more or less proportional to the factor (1 ± 0.5) [101]. CO% as such is useful for comparing folding rates of proteins of the same size, but it does not fit for comparing folding rates of small and large proteins, since CO% is reduced approximately proportionally to L^–1/3 along with growth of chain length L [65, 101, 102] (which reflects a low “entanglement” of chains of large proteins), whereas folding rate is reduced (while its TIME grows) with increasing proteins size (Fig. 5).

Therefore, parameter AbsCO = CO% × L, which increases with growth of chain length L as L^2/3 [101] and combines the effect of protein chain folding pattern [99, 102] with the main effect associated with the protein size, predicts well protein-folding rate.

5. In this review I allowed myself to omit numerous attempts to “bioinformatically” predict the rate of protein folding as, according to “blind” testing [103], they led to unsatisfactory results.

6. Returning to Levinthal’s paradox, one can conclude that it is resolved for protein chains under 100 a.a. in length (provided that their sequences allow significant stability for the only fold). This is because (i) these relatively short chains are able to cross the free-energy barrier in their pathway to their most stable folds regardless of their complexity (Fig. 5), and (ii) they are able to screen all their folds at the level of formation and assembly of ensembles of secondary structures (Fig. 9) and to find the most stable of them.

As to larger chains, they can screen only relatively simple (not much “entangled”) folds. Therefore, whether some other (very “entangled”) fold may be more stable than the native one is still an open question. This is actually observed for some “special” proteins similar to serpin, which consists of 400 a.a.

Acknowledgments

I am grateful to O. B. Ptitsyn, A. M. Gutin, and E. I. Shakhnovich for numerous fruitful discussions and my coauthors in works devoted to protein folding theory – A. Ya. Badretdinov, O. V. Galzitskaya, D. N. Ivankov, N. S. Bogatyreva, and S. A. Garbuzynskiy.

The first part of this work was supported by grants from the Howard Hughes Medical Institute and the program “Molecular and Cell Biology” of the Russian Academy of Sciences (projects Nos. 01200957492, 01201358029). Second part was supported by the Russian Science Foundation (project No. 14-24-00157).

REFERENCES

1.Anfinsen, C. B., Haber, E., Sela, M., and White, F. H., Jr. (1961) The kinetics of formation of native ribonuclease during oxidation of the reduced polypeptide chain, Proc. Natl. Acad. Sci. USA, 47, 1309-1314.
2.Stryer, L. (1975) Biochemistry, Vol. 1, W. H. Freeman and Company, San Francisco.
3.Creighton, T. E. (1991) Proteins, 2nd Edn., Chaps. 2 and 7, W. H. Freeman & Co, N.Y.
4.Kolb, V. A., Makeev, E. V., and Spirin, A. S. (1994) Folding of firefly luciferase during translation in a cell-free system, EMBO J., 13, 3631-3637.
5.Komar, A. A., Kommer, A., Krasheninnikov, I. A., and Spirin, A. S. (1997) Cotranslational folding of globin, J. Biol. Chem., 272, 10646-10651.
6.Eichmann, C., Preissler, S., Riek, R., and Deuerling, E. (2010) Cotranslational structure acquisition of nascent polypeptides monitored by NMR spectroscopy, Proc. Natl. Acad. Sci. USA, 107, 9111-9116.
7.Han, Y., David, A., Liu, B., Magadan, J. G., Bennink, J. R., Yewdell, J. W., and Qian, S.-B. (2012) Monitoring cotranslational protein folding in mammalian cells at codon resolution, Proc. Natl. Acad. Sci. USA, 109, 12467-12472.
8.Holtkamp, W., Kokic, G., Jager, M., Mittelstaet, J., Komar, A. A., and Rodnina, M. V. (2015) Cotranslational protein folding on the ribosome monitored in real time, Science, 350, 1104-1107.
9.Flanagan, J. M., Kataoka, M., Shortle, D., and Engelman, D. M. (1992) Truncated staphylococcal nuclease is compact but disordered, Proc. Natl. Acad. Sci. USA, 89, 748-752.
10.Wright, P. E., and Dyson, H. J. (1999) Intrinsically unstructured proteins: re-assessing the protein structure-function paradigm, J. Mol. Biol., 293, 321-331.
11.Uversky, V. N., Gillespie, J. R., and Fink, A. L. (2000) Why are “natively unfolded” proteins unstructured under physiologic conditions? Proteins, 41, 415-427.
12.Petsko, G. A., and Ringe, D. (2004) Protein Structure and Function, Chap. 1, New Science Press Ltd., London.
13.Ellis, R. J., and Hartl, F. U. (1999) Principles of protein folding in the cellular environment, Curr. Opin. Struct. Biol., 9, 102-110.
14.Libich. D. S., Tugarinov, V., and Clore, G. M. (2015) Intrinsic unfoldase/foldase activity of the chaperonin GroEL directly demonstrated using multinuclear relaxation-based NMR, Proc. Natl. Acad. Sci. USA, 112, 8817-8823.
15.Marchenko, N. Y., Marchenkov, V. V., Semisotnov, G. V., and Finkelstein, A. V. (2015) Strict experimental evidence that apo-chaperonin GroEL does not accelerate protein folding, although it does accelerate one of its steps, Proc. Natl. Acad. Sci. USA, 112, E6831-E6832.
16.Marchenkov, V. V., Sokolovsky, I. V., Kotova, N. V., Galitskaya, O. V., Bochkareva, E. S., Girshovich, A. S., and Semisotnov, G. V. (2004) Interaction of chaperone GroEL with early kinetic intermediates of renaturing proteins inhibits formation of their native structure, Biophysics, 49, 888-895.
17.Marchenko, N. Y., Garbuzynskiy, S. O., and Semisotnov, G. V. (2009) Molecular chaperones under normal and pathological conditions, in Molecular Pathology of Proteins (Zabolotny, D. I., ed.) Nova Science Publishers, New York, pp. 57-89.
18Anfinsen, C. B. (1973) Principles that govern the folding of protein chains, Science, 181, 223-230.
19.Gutte, B., and Merrifield, R. B. (1969) The total synthesis of an enzyme with ribonuclease A activity, J. Am. Chem. Soc., 91, 501-502.
20.Levinthal, C. (1968) Are there pathways for protein folding? J. Chim. Phys. Chim. Biol., 65, 44-45.
21.Levinthal, C. (1969) How to fold graciously, in Mössbauer Spectroscopy in Biological Systems: Proc. of a Meeting held at Allerton House, Monticello, Illinois (Debrunner, P., Tsibris, J. C. M., and Munck, E., eds.) Urbana-Champaign, IL, University of Illinois Press, pp. 22-24.
22.Privalov, P. L. (1979) Stability of proteins: small globular proteins, Adv. Protein Chem., 33, 167-241.
23.Sali, A., Shakhnovich, E., and Karplus, M. (1994) Kinetics of protein folding. A lattice model study of the requirements for folding to the native state, J. Mol. Biol., 235, 1614-1636.
24.Abkevich, V. I., Gutin, A. M., and Shakhnovich, E. I. (1994) Specific nucleus as a transition state for protein folding: evidence from the lattice model, Biochemistry, 33, 10026-10031.
25.Phillips, D. C. (1966) The three-dimensional structure of an enzyme molecule, Sci. Am., 215, 78-90.
26.Goldenberg, D. P., and Creighton, T. E. (1983) Circular and circularly permuted forms of bovine pancreatic trypsin inhibitor, J. Mol. Biol., 165, 407-413.
27.Grantcharova, V. P., Riddle, D. S., Santiago, J. V., and Baker, D. (1998) Important role of hydrogen bonds in the structurally polarized transition state for folding of the src SH3 domain, Nat. Struct. Biol., 5, 714-720.
28.Wetlaufer, D. B. (1973) Nucleation, rapid folding, and globular intrachain regions in proteins, Proc. Natl. Acad. Sci. USA, 70, 697-701.
29.Fulton, K. F., Main, E. R. G., Dagett, V., and Jackson, S. E. (1999) Mapping the interactions present in the transition state for unfolding/folding of FKBP12, J. Mol. Biol., 291, 445-461.
30.Ptitsyn, O. B. (1973) Stepwise mechanism of organization of protein molecules, Dokl. Acad. Nauk SSSR, 210, 1213-1215.
31.Ptitsyn, O. B. (1995) Molten globule and protein folding, Adv. Protein Chem., 47, 83-229.
32.Privalov, P. L. (1996) Intermediate states in protein folding, J. Mol. Biol., 258, 707-725.
33.Fersht, A. (1999) Structure and Mechanism in Protein Science: A Guide to Enzyme Catalysis and Protein Folding, Chaps. 2, 15, 18, and 19, W. H. Freeman & Co., N.Y.
34.Melnik, B. S., Marchenkov, V. V., Evdokimov, S. R., Samatova, E. N., and Kotova, N. V. (2008) Multi-state protein: determination of carbonic anhydrase free-energy landscape, Biochem. Biophys. Res. Commun., 369, 701-706.
35.Finkelstein, A. V., and Ptitsyn, O. B. (2016) Protein Physics. A Course of Lectures, 2nd Edn., Chaps. 7, 10, 13, 18, and 19-21, Academic Press, an Imprint of Elsevier Science, Amsterdam-Boston-Heidelberg-London-New York-Oxford-Paris-San Diego-San Francisco-Singapore-Sydney-Tokyo.
36.Leopold, P. E., Montal, M., and Onuchic, J. N. (1992) Protein folding funnels: a kinetic approach to the sequence-structure relationship, Proc. Natl. Acad. Sci. USA, 89, 8721-8725.
37.Wolynes, P. G., Onuchic, J. N., and Thirumalai, D. (1995) Navigating the folding routes, Science, 267, 1619-1620.
38.Dill, K. A., and Chan, H. S. (1997) From Levinthal to pathways to funnels, Nat. Struct. Biol., 4, 10-19.
39.Bicout, D. J., and Szabo, A. (2000) Entropic barriers, transition states, funnels, and exponential protein folding kinetics: a simple model, Protein Sci., 9, 452-465.
40.Tanford, C. (1968) Protein denaturation, Adv. Protein Chem., 23, 121-282.
41.Creighton, T. E. (1978) Experimental studies of protein folding and unfolding, Prog. Biophys. Mol. Biol., 33, 231-297.
42.Shakhnovich, E. I., and Gutin, A. M. (1990) Implications of thermodynamics of protein folding for evolution of primary sequences, Nature, 346, 773-775.
43.Gutin, A. M., and Shakhnovich, E. I. (1993) Ground state of random copolymers and the discrete random energy model, J. Chem. Phys., 98, 8174-8177.
44.Galzitskaya, O. V., and Finkelstein, A. V. (1995) Folding of chains with random and edited sequences: similarities and differences, Protein Eng., 8, 883-892.
45.Shakhnovich, E. I. (2006) Protein folding thermodynamics and dynamics: where physics, chemistry, and biology meet, Chem. Rev., 106, 1559-1588.
46.Bryngelson, J. D., and Wolynes, P. G. (1989) Intermediates and barrier crossing in a random energy model (with applications to protein folding), J. Phys. Chem., 93, 6902-6915.
47.Go, N., and Abe, H. (1981) Noninteracting local-structure model of folding and unfolding transition in globular proteins. I. Formulation, Biopolymers, 20, 991-1011.
48.Ngo, J. T., and Marks, J. (1992) Computational complexity of a problem in molecular structure prediction, Protein Eng., 5, 313-321.
49.Unger, R., and Moult, J. (1993) Finding the lowest free energy conformation of a protein is an NP-hard problem: proof and implications, Bull. Math. Biol., 55, 1183-1198.
50.Karplus, M. (1997) The Levinthal paradox: yesterday and today, Fold. Des., 2, Suppl. 1, S69-S75.
51.Nolting, B. (2010) Protein Folding Kinetics: Biophysical Methods, Chaps. 10-12, Springer, N.Y.
52.Bogatyreva, N. S., and Finkelstein, A. V. (2001) Cunning simplicity of protein folding landscapes, Protein Eng., 14, 521-523.
53.Zwanzig, R., Szabo, A., and Bagchi, B. (1992) Levinthal’s paradox, Proc. Natl. Acad. Sci. USA, 89, 20-22.
54.Finkelstein, A. V. (2002) Cunning simplicity of a hierarchical folding, J. Biomol. Struct. Dyn., 20, 311-313.
55.Finkelstein, A. V., and Badretdinov, A. Ya. (1997) Physical reasons for fast folding of stable protein spatial structure: resolution of the Levinthal’s paradox, Mol. Biol., 31, 469-477.
56.Finkelstein, A. V., and Badretdinov, A. Ya. (1997) Rate of protein folding near the point of thermodynamic equilibrium between the coil and the most stable chain fold, Fold. Des., 2, 115-121.
57.Wolynes, P. G. (1997) Folding funnels and energy landscapes of larger proteins within the capillarity approximation, Proc. Natl. Acad. Sci. USA, 94, 6170-6175.
58.Gutin, A. M., Abkevich, V. I., and Shakhnovich, E. I. (1996) Chain length scaling of protein folding time, Phys. Rev. Lett., 77, 5433-5436.
59.Zana, R. (1975) On the rate determining step for helix propagation in the helix–coil transition of polypeptides in solution, Biopolymers, 14, 2425-2428.
60.Eyring, H. (1935) The activated complex in chemical reactions, J. Chem. Phys., 3, 107-115.
61.Pauling, L. (1970) General Chemistry, Chap. 16, W. H. Freeman & Co, Ltd.
62.Emmanuel, N. M., and Knorre, D. G. (1984) Course of Chemical Kinetics [in Russian], 4th Edn., Chaps. III and V (§§ 2 and 3), Vysshaya Shkola, Moscow.
63.Landau, L. D., and Lifshits, E. M. (1964) Statistical Physics [in Russian], Nauka, Moscow, p. 150.
64.Galzitskaya, O. V., and Finkelstein, A. V. (1999) A theoretical search for folding/unfolding nuclei in three-dimensional protein structures, Proc. Natl. Acad. Sci. USA, 96, 11299-11304.
65.Garbuzynskiy, S. O., Ivankov, D. N., Bogatyreva, N. S., and Finkelstein, A. V. (2013) Golden triangle for folding rates of globular proteins, Proc. Natl. Acad. Sci. USA, 110, 147-150.
66.Finkelstein, A. V., Badretdin, A. J., Galzitskaya, O. V., Ivankov, D. N., Bogatyreva, N. S., and Garbuzynskiy, S. O. (2017) There and back again: two views on the protein folding puzzle, Phys. Life Rev., doi: 10.1016/j.plrev.2017.01.025.
67.Shakhnovich, E. I., and Finkelstein, A. V. (1982) To the theory of cooperative transitions in proteins, Dokl. AN SSSR, 267, 1247-1250.
68.Jacobson, H., and Stockmayer, W. (1950) Intramolecular reaction in polycondensations. I. The theory of linear systems, J. Chem. Phys., 18, 1600-1606.
69.Flory, P. (1969) Statistical Mechanics of Chain Molecules, Chap. 3, Wiley-Interscience, New York.
70.Fu, B., and Wang, W. (2004) A 2^{0(n^1-1/d·log(n))} time algorithm for d-dimensional protein folding in the HP-model, Lecture Notes Comp. Sci., 3142, 630-644.
71.Steinhofel, K., Skaliotis, A., and Albrecht, A. A. (2006) Landscape analysis for protein folding simulation in the H-P model, Lecture Notes Comp. Sci., 4175, 252-261.
72.Finkelstein, A. V., and Badretdinov, A. Ya. (1998) Influence of chain knotting on the rate of folding, Fold. Des., 3, 67-68.
73.Galzitskaya, O. V., Ivankov, D. N., and Finkelstein, A. V. (2001) Folding nuclei in proteins, FEBS Lett., 489, 113-118.
74.Rollins, G. C., and Dill, K. A. (2014) General mechanism of two-state protein folding kinetics, J. Am. Chem. Soc., 136, 11420-11427.
75.Finkelstein, A. V. (2017) Some additional remarks to the solution of the protein folding puzzle: Reply to comments on “There and back again: two views on the protein folding puzzle”, Phys. Life Rev., doi: 10.1016/j.plrev.2017.06.025.
76.Bychkova, V. E., Semisotnov, G. V., Balobanov, V. A., and Finkelstein, A. V. (2018) Molten globule: 45 years later, Biochemistry (Moscow), 83, Suppl.1, S33-S47.
77.Debe, D. A., Carlson, M. J., and Goddard, W. A., 3rd. (1999) The topomer-sampling model of protein folding, Proc. Natl. Acad. Sci. USA, 96, 2596-2601.
78.Makarov, D. E., and Plaxco, K. W. (2003) The topomer search model: a simple, quantitative theory of two-state protein folding kinetics, Protein Sci., 12, 17-26.
79.Levitt, M., and Chothia, C. (1976) Structural patterns in globular proteins, Nature, 261, 552-558.
80.Chothia, C., and Finkelstein, A. V. (1990) The classification and origins of protein folding patterns, Ann. Rew. Biochem., 59, 1007-1039.
81.Finkelstein, A. V., and Ptitsyn, O. B. (2012) Proteins Physics. Lection Course with Colored and Stereoscopic Illustrations and Tasks [in Russian], 4th Edn., Chaps. 7, 10, 13, and 18-21, Knizhny Dom “Universitet”, Moscow.
82.Finkelstein, A. V., and Garbuzynskiy, S. O. (2015) Reduction of the search space for the folding of proteins at the level of formation and assembly of secondary structures: a new view on solution of Levinthal’s paradox, ChemPhysChem, 16, 3373-3378.
83.Murzin, A. G., and Finkelstein, A. V. (1988) General architecture of α-helical globule, J. Mol. Biol., 204, 749-770.
84.Crick, F. H. C. (1953) The packing of α-helices: simple coiled coils, Acta Crystallogr., 6, 689-697.
85.Ptitsyn, O. B., and Finkelstein, A. V. (1980) Similarities of protein topologies: evolutionary divergence, functional convergence or principles of folding? Quart. Rev. Biophys., 13, 339-386.
86.Ptitsyn, O. B., and Finkelstein, A. V. (1970) Connection between secondary structure of globular proteins and their primary structure, Biofizika, 15, 757-767.
87.Jones, D. T. (1999) Protein secondary structure prediction based on position-specific scoring matrices, J. Mol. Biol., 292, 195-202.
88.Finkelstein, A. V., and Garbuzynskiy, S. A. (2016) Solution of Levinthal’s paradox is possible at the level of the formation and assembly of protein secondary structures, Biophysics, 61, 1-5.
89.Munoz, V., Thompson, P. A., Hofrichter, J., and Eaton, W. A. (1997) Folding dynamics and mechanism of beta-hairpin formation, Nature, 390, 196-199.
90.Mukherjee, S., Chowdhury, P., Bunagan, M. R., and Gai, F. (2008) Folding kinetics of a naturally occurring helical peptide: implication of the folding speed limit of helical proteins, J. Phys. Chem. B, 112, 9146-9150.
91.Finkelstein, A. V. (2015) Two views on the protein folding puzzle (http://atlasofscience.org/two-views-on-the-protein-folding-puzzle/).
92.Shakhnovich, E. I., and Gutin, A. M. (1989) Formation of unique structure in polypeptide-chains theoretical investigation with the aid of a replica approach, Biophys. Chem., 34, 187-199.
93.Finkelstein, A. V. (2014) Physics of Protein Molecules [in Russian], Chap. 9, ANO “Izhevsk Institute of Computational Studies”, Moscow-Izhevsk.
94.Ubbelode, A. (1965) Melting and Crystal Structure, Clarendon Press, UK.
95.Slezov, V. V. (2009) Kinetics of First-Order Phase Transitions, Chaps. 3-5, and 8, Wiley-VCH, Weiheim.
96.Thirumalai, D. (1995) From minimal models to real proteins: time scales for protein folding kinetics, J. Phys. I. (Orsay, Fr.), 5, 1457-1469.
97.Murzin, A. G. (2008) Metamorphic proteins, Science, 320, 1725-1726.
98.Tsutsui, Y., Cruz, R. D., and Wintrode, P. L. (2012) Folding mechanism of the metastable serpin α1-antitrypsin, Proc. Natl. Acad. Sci. USA, 109, 4467-4472.
99.Plaxco, K. W., Simons, K. T., and Baker, D. (1998) Contact order, transition state placement and the refolding rates of single domain proteins, J. Mol. Biol., 277, 985-994.
100.Nolting, B., Schalike, W., Hampel, P., Grundig, F., Gantert, S., Sips, N., Bandlow, W., and Qi, P. X. (2003) Structural determinants of the rate of protein folding, J. Theor. Biol., 223, 299-307.
101.Ivankov, D. N., Garbuzynskiy, S. O., Alm, E., Plaxco, K. W., Baker, D., and Finkelstein, A. V. (2003) Contact order revisited: influence of protein size on the folding rate, Protein Sci., 12, 2057-2062.
102.Ivankov, D. N., Bogatyreva, N. S., Lobanov, M. Yu., and Galzitskaya, O. V. (2009) Coupling between properties of the protein shape and the rate of protein folding, PLoS One, 4, e6476.
103.Corrales, M., Cusco, P., Usmanova, D. R., Chen, H. C., Bogatyreva, N. S., Filion, G. J., and Ivankov, D. N. (2015) Machine learning: how much does it tell about protein folding rates? PLoS One, 10, e0143166.