Coefficient of Variation of Lifespan Across the Tree of Life: Is It a Signature of Programmed Aging?
G. A. Shilovsky1,2*, T. S. Putyatina2, V. V. Ashapkin1, O. S. Luchkina3, and A. V. Markov2
1Belozersky Institute of Physico-Chemical Biology, Lomonosov Moscow State University, 119991 Moscow, Russia; E-mail: gregory_sh@list.ru, gr_gerontol@gmail.com2Lomonosov Moscow State University, Faculty of Biology, 119991 Moscow, Russia
3Severtsov Institute of Ecology and Evolution, Russian Academy of Sciences, 119071 Moscow, Russia
* To whom correspondence should be addressed.
Received August 9, 2017; Revision received September 15, 2017
Measurements of variation are of great importance for studying the stability of pathological phenomena and processes. For the biology of aging, it is very important not only to determine average mortality, but also to study its stability in time and the size of fluctuations that are indicated by the variation coefficient of lifespan (CVLS). It is believed that a relatively small (~20%) value of CVLS in humans, comparable to the coefficients of variation of other events programmed in ontogenesis (for example, menarche and menopause), indicates a relatively rigid determinism (N. S. Gavrilova et al. (2012) Biochemistry (Moscow), 77, 754-760). To assess the prevalence of this phenomenon, we studied the magnitude of CVLS, as well as the coefficients of skewness and kurtosis in diverse representatives of the animal kingdom using data provided by the Institute for Demographic Research (O. R. Jones et al. (2014) Nature, 505, 169-173). We found that, unlike humans and laboratory animals, in most examined species the values of CVLS are rather high, indicating heterogeneity of the lifespan in the cohorts studied. This is probably due to the large influence of background mortality, as well as the non-monotonicity of total mortality in the wild, especially at the earliest ages. One way to account for this influence is to “truncate” the data (removing the earliest and latest ages from consideration). To reveal the effect of this procedure, we proposed a new indicator, the stability coefficient of mortality dynamics, which indicates how quickly CVLS is reduced to values that characterize a relatively homogeneous population (33%) when the data are “truncated”. Such indicators facilitate the use of the parameters of survival curves for analysis of the effects of geroprotectors, lifestyle, and other factors on lifespan, and for the quantification of relative contributions of genetic and environmental factors to the dynamics of aging in human and animal populations, including those living in the wild.
KEY WORDS: aging, lifespan, mortality rate, survival curves, skewness, coefficient of variationDOI: 10.1134/S0006297917120070
Abbreviations: CV, coefficient of variation; LS, lifespan.
Organism aging is manifested biologically in the appearance of
age-related diseases, decrepitude, organism deterioration, and
mathematically in age-related increase in death probability [1]. If this parameter (probability of an
organism’s death) depended entirely on the degree of its
“wear” growing with age, then the mortality rate of
multicellular organisms should have been increasing with age regardless
of the position of the species on the evolutionary tree. However, great
differences in the dynamics of mortality in different species
(increasing, constant, decreasing, convex and concave mortality
trajectories, both in long- and short-lived species) have been found
[2-4]. V. P. Skulachev pointed
to this contradiction and proposed the concept of programmed death [5]. According to this concept, there is a fast
programmed death of the organism (acute phenoptosis) or death caused by
triggering the genetic self-elimination program of the individual
(chronic phenoptosis). Thus, according to this concept, aging can be
considered as a slow (chronic) phenoptosis. “Programmed
aging” is understood as a set of step-by-step instructions
(cascades) recorded in the genome. These cascades could develop due to
selection supporting genetic variants that provided optimal rates of
age-related decrease in viability. Computer models have been developed
demonstrating evolutionary benefit of phenoptosis in certain situations
[6]. It is important to note that recently the
process of phenoptosis contributing to the survival of a population
under unfavorable conditions has been described in the ascidium
Botrylloides leachii (subtype tunicates, type chordates) [7]. The so-called temporal scaling phenomenon also
speaks in favor of the existence of individual cascades that control
mortality (see below).
Historically, the fact that properties developing after the end of the reproduction period are not subject to natural selection was seen as the main objection to the concept of aging resulting from adaptive evolution [8-10]. In fact, in many animals (and especially in social ones), skills useful to the population and acquired in the post-reproductive period, are transferred to reproductive individuals during training, increasing their fitness, and, in general, increase the resistance of the population to environmental impact [11]. In social species with developed cultural (social) inheritance, selection should support “genes of longevity”. The longer the older generation lives, the more it educates young individuals, including their own descendants [12]. The group of social animals with intersecting young and old generations includes not only mammals, but also many social insects, birds, and some other organisms.
Another mechanism of the possible inheritance of post-reproduction properties is associated with the correlation of the organisms’ properties and gene pleiotropy. “Genes of longevity”, being correlated with some adaptive feature, can therefore be fixed in the population. Pleiotropy can be used to postulate the presence of genes that enhance reproductive success at a young age despite their delayed negative effects in old age [13-15]. This hypothesis is confirmed, for example, by the phenomenon of aging of dividing cells (irreversible cessation of division of damaged cells), which stimulates viability at an early age by decreasing the incidence of cancer and at the same time limits lifespan due to the accumulation of senescent cells [16-18].
If we consider aging as slow (chronic) phenoptosis, then the increasing or weakening of mechanisms contributing (or hindering) this process in consecutive generations can be seen as the evolution of aging. If longevity is supported by selection, organisms can develop special protective and repair systems that slow chronic phenoptosis. Since lifespan is the same stable species characteristic as body size or fecundity, lifespan (i.e., the moment of death), as well as its mechanisms, should be at least partially programmed in the genome [19, 20].
Weismann [21] considered limitation of the number of divisions of somatic cells (unlike unrestrictedly proliferating germ cells) to be the biological mechanism of such a program. He explained the interspecific differences in animal lifespan by a different number of cellular generations. Presence of programmed aging is confirmed by the appearance of the so-called “longevity programs” based on genes that support an organism’s survival by repair of somatic cells [15]. Knockout of repair genes results in decreased lifespan and accelerated aging. This program can act alongside the known mechanisms of aging, which can even be a part of it. Septic shock is an example of pathology showing signs of phenoptosis. Apparently, rapid fatal outcome (due to mass ejection of apoptosis-inducing cytokines by macrophages) is specially organized by the infected organism to prevent the development of an epidemic [5]. Programmed aging is also confirmed by the discovery of dozens of mutations that increase lifespan and affect the organism’s resistance to stress [22-25].
Many experimental data suggest that aging is accompanied and probably determined by epigenetic changes (epigenetic program and transcription “signatures” of aging) [26, 27]. A longevity program could have developed in evolution to adapt to short-term extreme external influences (fluctuations in temperature/humidity, amount of food resources) that prevented reproduction [15, 22]. We know an example when in a population of opossums that accidentally populated a separate islet, the average lifespan increased and physiological aging (determined by collagen structure of the tail tendons) slowed compared to “mainland” animals [28].
Thus, the concept suggested by V. P. Skulachev combines Weismann’s hypothesis of aging as an adaptive mechanism of programmed death with an alternative view of aging being the result of accumulation of lesions and errors [5, 29].
The assertion that time variation of aging-related events is much greater than that of ontogeny-programmed events is one of the arguments of the opponents of the programmed aging theory. Thus, the main task of N. S. Gavrilova, L. A. Gavrilov, F. F. Severin, and V. P. Skulachev [1] was to test the validity of this argument. They used the spread of lifespan values to assess the degree of its programming by comparing the CVLS with the CV of events associated with reproduction (ages of onset of menarche and menopause). The results of that work indicate that the values of CVLS as a measure of the extent to which the aging process and lifespan are “genetically programmed” are very promising. Since the article of N. S. Gavrilova et al. was dedicated to the parameters of lifespan distribution only in humans, it seems interesting to check the situation in other representatives of the animal kingdom, which is the subject of the present work.
Statistical study of the mathematical parameters of aging and choosing the most appropriate ways of describing them are important both for fundamental biology and for geriatrics [2, 4, 30-39]. Determination of the effectiveness of geroprotectors requires knowledge of the behavior of mortality curves at older ages. The choice of mathematical criteria for lifespan analysis should be approached with deep understanding of their biological meaning. For example, the well-known Gompertz equation does not always adequately describe the behavior of survival curves in the initial and final sections [3, 40]. Another of its drawbacks is that mortality is considered only at the population level. For all people in the same age range, death probability is the same. In addition, although, for example, measuring methylation of certain DNA loci makes it possible to determine biological, and not the passport age [26], successful attempts to overcome this discrepancy using such methods are still few.
For example, Mitnitski proposed to determine a parameter he called the frailty index (FI) instead of measuring death probability [39, 41]. Gavrilov [34] was the first to note that there is a certain transition of the organism from the “survivalist” to the “non-survivalist” state. Mitnitski has shown that this index varies with age similarly to death probability, but its growth is two times slower. It is based on approximately 30 indicators of health, measured in each person, thus being integrative. This indicator makes it possible to compare separate individuals with the group. It is interesting to note that, unlike death probability, FI does not grow to 100%, but only up to about 70%.
Jones et al. [2] analyzed mortality of animals and plants from the onset of puberty to the age corresponding to 95% extinction of the initial sexually mature cohort. The criterion chosen by them (ratio of mortality at the age corresponding to 95% cohort extinction to the average for the entire period studied) led to several clearly extravagant conclusions. For example, the great tit was attributed to non-aging species and placed next to hydra, although the tit simply does not have time to grow old due to high background mortality. Because of the impact of high background mortality, LS95 for pine was determined as 30 years, a tortoise was declared the most non-aging animal, while the crocodile was in the middle of the list, and the long-lived (Japanese) and animals capable of maintaining mortality at practically zero level for a very long time (southern fulmar) were attributed to the most aging species.
Jones’ method allows us to characterize mortality throughout the entire biologically significant part of the life cycle only for some species. As for long-lived species with a less pronounced increase (or even a decrease) in age-related mortality (for example, for Johnstone’s crocodile, hermit crab, or Scots pine), as well as animals with average lifespan that reach a 5% survival margin prior to physiological aging, Jones’ method allows characterization of only a small part of their life cycle and does not provide an opportunity to analyze manifestations of aging in its late stages. We concluded [42] that the classification proposed by Jones et al. [2], allows approximate divisions of animals and plants only based on the increase in age-related death probability, whereas it is necessary to develop more complex models for the assessment of susceptibility to physiological aging.
This article is devoted to analysis of both already known statistical parameters of animal lifespan distribution and parameters introduced by our group. We compare the two approaches to assessing the “stability of dynamics” of mortality (its background and age-dependent components), which we call the spread and monotonicity of mortality change in age intervals.
Akif’ev and Potapenko noted that although in nature probabilities of many events have a normal distribution, the dynamics of mortality significantly differs from Gauss distribution (curves of lifespan distribution have a non-zero excess (a peakedness) and asymmetry) [43]. They conclude that death results not only from random processes (for example, accumulation of damage), but also from the operation of a certain mechanism, and thus the coincidence of survival curves suggests that the mechanisms of aging and death of various species have some common basis [43]. At the same time, the normality of lifespan distribution in case of mortality being the consequence of only random processes, in our opinion, is not unambiguous.
To characterize lifespan distribution, we used the coefficient of variation of lifespan (CVLS), since this parameter was shown to have an important biological meaning [1].
Gavrilova et al. [1] verified the well-known assertion that the spread of individual lifespan and the timing of the onset of aging-related events significantly exceeds the spread of the onset of events associated with the development program. To do that, the authors compared the variability (CV) of parameters determined by the development program of the organism (age at puberty onset) and parameters related to aging (age at the onset of menopause and death) using data from the National Survey of Midlife Development in United States (MIDUS). It was found that for age of puberty onset CV = 8-13%, for age of menopause onset CV = 7-11%, and for age of death CV = 16-21%. Thus, Gavrilova et al. showed that relative variability of age of death is similar in magnitude to the relative variability of the age of puberty and the onset of menopause [1]. Thus, the “programming” of lifespan (as the age of death) was also shown by statistical methods.
Now most authors to some extent recognize the role of genetic programs in the determination of longevity and aging [44-50].
In addition, Stroustrup et al. suggested [37] that we can observe in compared cohorts the phenomenon of temporal scaling, when a certain impact only slows or accelerates the process of changing mortality with age, without changing the shape of the survival curve.
When studying lifespan as one of the organism’s characteristics, it is suggested that if the degree of its genetic regulation is low (lifespan is poorly determined), then one should expect a high spread in lifespan in the studied population [1]. On the other hand, if lifespan regulation by the genome is high, then lifespan variability in the population should be lower.
Another difficulty in interpreting the degree of lifespan programming based on CVLS is because the ratio of the contribution of genes and non-genetic component (environment + stochastics) to variability of a given trait in each individual is not a constant, but depends on the circumstances. It is obvious that the same allele can reduce animal lifespan under adverse conditions, but have no effect on the lifespan in ideal conditions. Genes that affect lifespan of Indians might have no effect on the lifespan of Japanese. For example, in a society with no hard physical labor, the gene affecting the wear rate of joints or any other organs important in heavy physical work does not affect aging, but in primitive society, it surely does. Thus, habitat conditions can radically change the system of lifespan genetic determination in the same species.
It should also be taken into account that phenotypic manifestation of a gene (or a group of genes responsible for the trait) can vary in the degree of manifestation of this trait (the gene can manifest itself in varying degrees). This phenomenon is called gene expressivity. The action of a gene can be rather constant, persistent in its manifestation, or unstable, variable. We quite often encounter variability of gene expressivity in different organisms. In Drosophila, mutation of the eyeless gene results in the appearance of a mutant form with a strongly reduced number of facets. However, when looking at the offspring of one parental couple, when all the flies bear this mutation, one can see that in some flies the eyes are almost completely devoid of facets, while in others the number of eye facets reaches half the normal number. The same phenomenon is observed in relation to many properties in other animals and plants [51].
One and the same trait can be manifested in some, but not in other individuals (penetrance). With full penetrance (100%), the mutant gene manifests itself in every individual; with incomplete penetrance (less than 100%), the gene manifests its phenotypic effect in a certain percentage of individuals. Expressivity and penetrance are caused by gene interaction in the genotype and various reactions of the latter to the environmental factors affecting the course of ontogenesis [51].
MATERIALS AND METHODS
In this work, we have evaluated various approaches by comparing statistical parameters of lifespan distribution based on data from the Max Planck Institute for Demographic Research (Germany), which were provided in Jones et al. [2].
These data characterize the quantitative distribution of individuals by lifespan value, i.e., percentage or fraction of individuals that died in each age interval (with the base interval for vertebrates usually being 1 year, for invertebrates 1 day). The level of variability of lifespan distribution CVLS was analyzed for Japanese females, Swedish females, and Aché Indians, as well as for 23 animal species – 18 vertebrates and 5 invertebrates (see the table). Species from different systematic groups were considered: invertebrates – 5 species (3 types), bony fish – 1 species, reptiles – 3 species from all 3 orders, birds – 7 species from 5 orders, mammals – 8 species from 3 orders (4 species of rodents, 1 species of cetaceans, and 3 species of primates). Among the primates, the species Homo sapiens is represented by Japanese females and Indians (Mongoloid race) and Swedish females (Caucasoid race). All the examined species differed in the size of the sample (the cohort used to determine the parameters of mortality and lifespan distribution), living conditions (in the wild, captivity), and geographical distribution (i.e., environmental conditions).
Parameters of animal lifespan distribution
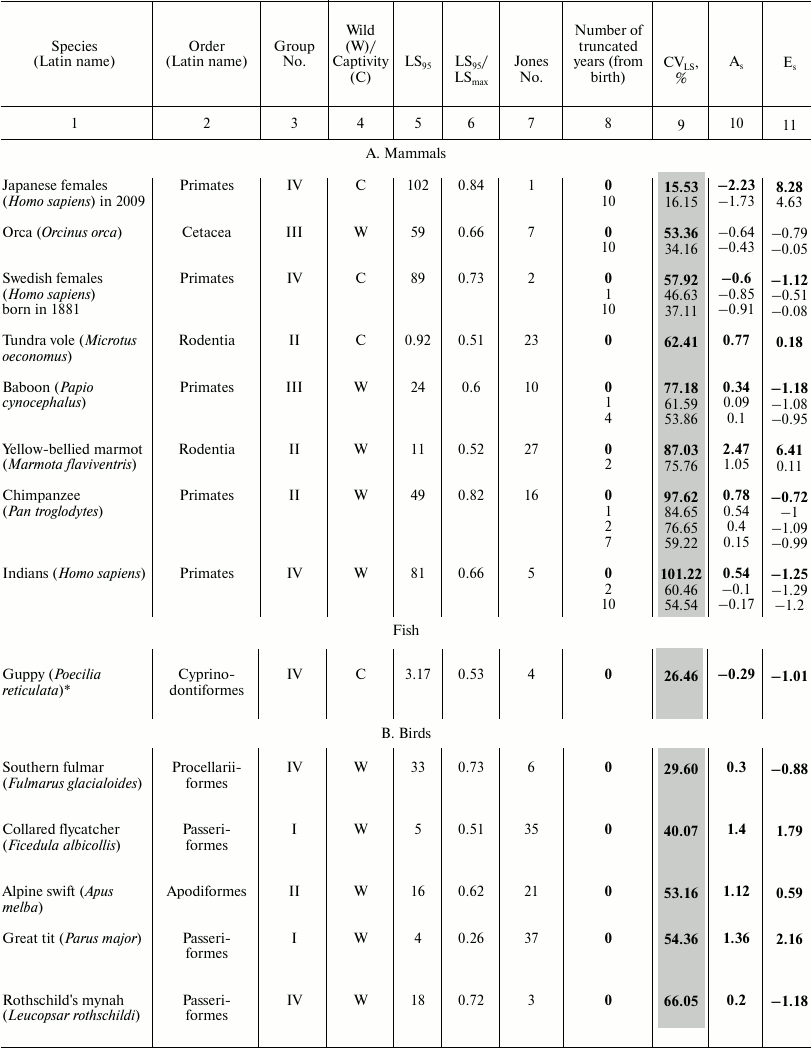
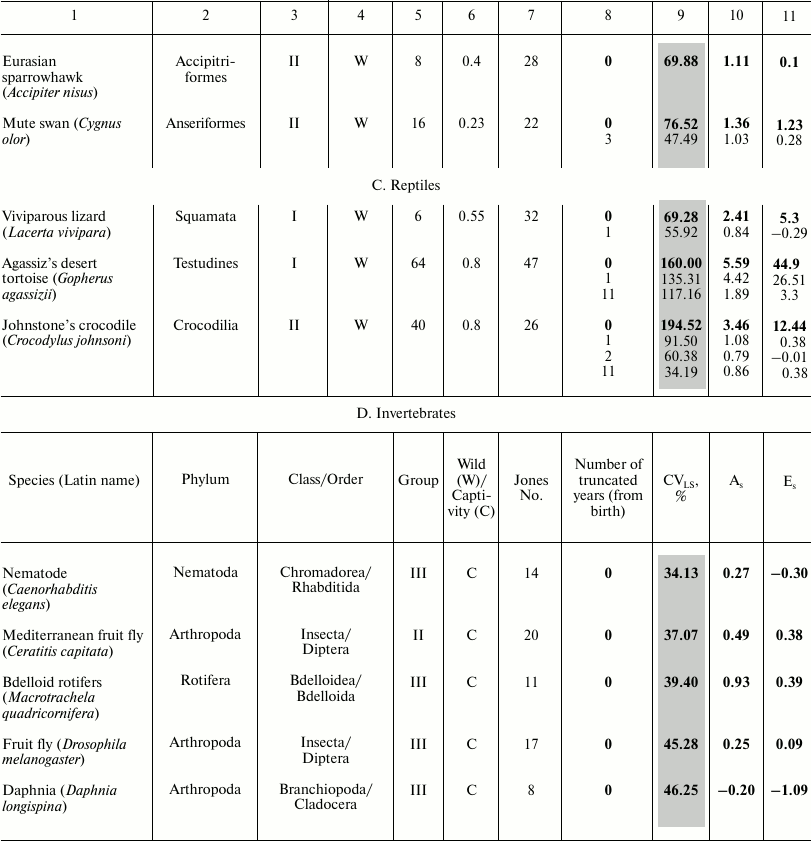
Note: Coefficients of variation (CVLS), skewness
(As), and kurtosis (Es) of lifespan (LS) in
vertebrates (A-C) and invertebrates (D). LS95
corresponds to the age when only 5% of the cohort remain alive;
LSmax – maximum LS; C – animals
were observed in captivity, W – in the wild;
CVLS – coefficient of variation of lifespan;
As – coefficient of skewness;
Es – coefficient of kurtosis. Values for the
complete cohort are shown in bold. Vertebrate species within each class
(1A-C) and invertebrates (1D) are grouped according to increase in CV
in the complete cohort and within the species (if conducted)
– by the truncation size (increase in number of years (from
birth) excluded from consideration).
* Fish.
The following parameters were considered: CVLS, coefficients of skewness (As) and kurtosis (Es). The data were rounded up to the second decimal place. Data were processed using Statistica 11. The results are shown in the table (A-D). Additional CV studies were performed using Excel 2007 software.
To compare the main regularities of the aging process in animals located on different branches of the evolutionary tree, we sorted the survival data of 46 species published by the Institute for Demographic Research (Germany) [2]. We numbered all the examined species in the same way as they are mentioned in the text of the original article [2] (from 1 to 48 based on the decrease in the ratio of mortality at the age of 5% survival to the average mortality) and subdivided them into four large groups, where group I includes species with the lowest age-related change in mortality, and IV embraces species with the highest change ([42] and the table).
For vertebrates, we calculated the ratio of the value of LS95 to the maximal LS (see table) so that to determine to what extent the lifespan corresponding to the time when only 5% of the cohort remains alive (LS95) characterizes the life cycle of a particular species. Data on other species are unfortunately incomplete and contradictory, and quite often the value of the maximal lifespan from the databases was lower than LS95 provided by Jones (see, for example, [52]). The values of the maximum LS (unless otherwise indicated) were taken from the database of the Institute for Demographic Research (Rostock, Germany/Odense, Denmark) [2, 53].
The table also indicates whether the animals were observed in the wild or in captivity. To avoid the widespread objection that there is no aging in the wild and this phenomenon is manifested only in laboratory conditions, Jones [2] presents data on animals that live in the wild (mainly in national parks), except for laboratory animals (fruit flies, nematode), as well as such animals as rotifers, voles – in this case registration of the demographic structure in the wild is not possible.
Statistical parameters and their properties. Left-sided skewness may indicate the existence of a variety of genetic and environmental factors that allow an individual to die at an earlier age, while delaying death is much more difficult [1]. In the case of right-sided skewness, higher values of the trait prevail, and this may indicate the existence of many genetic and environmental factors that increase the survival of individuals at a young age, which in turn can lead to the selection of “worthy” representatives of the species that leave more descendants. All substandard and unadapted, as well as the “unlucky” individuals, die at an earlier age. Those who have reached older age (in some species also bigger size) can apparently relieve the pressure of factors that do not depend on the individual itself; we can assume that their subsequent survival depends on their own genetic component (at least in case of pronounced right-sided asymmetry).
A large (in modulus) kurtosis indicates a significant difference in distribution compared to normal. Positive kurtosis suggests that the distribution has a steeper peak. In this case, the values of the characteristics that are close to the mean value prevail. We can say that the higher the value of kurtosis, the narrower the interval of intensive extinction of a population.A negative kurtosis indicates that the values of the characteristic are not concentrated in the middle range but are distributed more evenly, or there are several peaks in the distribution. The smaller the kurtosis value, the more evenly mortality is distributed over the ages, or there are several age intervals with increased mortality.
High CVLS means the presence of strong lifespan heterogeneity (genetically determined and environmental). Low CVLS indicates low cohort heterogeneity in relation to lifespan (this may be facilitated, for example, by a low level of background mortality).
In addition, for species with high CVLS values (>33%, indicating sample heterogeneity in relation to lifespan, apparently associated with a greater effect of background mortality, and also with nonmonotonicity of total mortality in the wild, especially at the earliest ages), we proposed a new indicator in order to reveal the effect of one of the most well-known ways to take into account this impact (“data truncation”, that is, removal of the earliest and latest ages from consideration): coefficient of mortality dynamics stability, which demonstrates how quickly after truncation CVLS is reduced to values characteristic of a relatively homogeneous population (33%). The effect of truncation of age intervals on CVLS change was checked. To do this, age intervals were consecutively deleted, and CVLS values in the remaining samples were determined. Removal of age intervals resulted in CVLS decrease. They were removed until CVLS became equal to 33%. T1 is the age at which CVLS drops to 33% after consecutive truncation of initial intervals. T2 is the age at which CVLS drops to 33% after consecutive truncation of final intervals. The coefficient was determined as the ratio of the described ages (T2 and T1).
RESULTS AND DISCUSSION
Data on lifespan distribution is presented in the table (A-D). They are grouped according to increase in CVLS. For comparison, the table shows classification based on increase in the number according to Jones et al. [2] (by the ratio of mortality rate at the age of 5% survival to the mean for the entire studied period, i.e., from puberty to the age corresponding to 5% survival, within each class).
We revealed that, in contrast to humans and laboratory animals, high CVLS values are characteristic for most of the examined species, indicating the heterogeneity of samples in relation to lifespan. Apparently, this is due to the greater effect of background mortality, as well as to the nonmonotonicity of overall mortality in the wild, especially at the earliest ages.
Gavrilova et al. [1] rightly argue that data on total mortality include also the so-called unnatural mortality from external causes (accidents, suicide, etc.). To exclude child mortality, they suggest “truncating”, that is, studying the cohort not at its entirety, but only starting from the age of ten, since this is the age when mortality starts increasing, that is, it can be considered the age of the onset of aging. Jones et al. [2] also truncated data, starting to calculate mortality at puberty (respectively, 12, 13, and 15 years for Indians, Swedish females, and Japanese females, respectively). Nevertheless, it can be noted that this truncation did not always lead to decrease in CVLS level to values indicating sample homogeneity in relation to a studied characteristic (see table).
The lowest CVLS value was observed in Japanese females: for a full cohort, CVLS = 15.53%, i.e., the population is extremely homogeneous (table, part A). These data coincide with the data of Gavrilova et al. [1]. Infant mortality is not expressed. A significant increase in mortality is observed only at an older age, over 50 years: As = −2.23, Es = 8.28 – anomalously high value of the indicator, pronounced concentration of values near the median, significant left-sided skewness. In the cohort without individuals that died in the first 10 years of their life, CVLS and As hardly changed, and the peakedness declined.
A study [1] showed left-sided skewness also for American females: As = −1.81 for the entire population (–1.26 for mortality at age of over 10 years). In case of left-sided skewness, the tail of the left side of the distribution is longer than the tail of the right side, and the bulk of the data (including the peak of the most probable age of death) is to the right of the mean value, i.e., many genetic and environmental factors accelerate the onset of aging, while delaying this process is much more difficult [1].
In Swedish females, CVLS = 57.92% for the full cohort, i.e., the population is heterogeneous, and there is high mortality rate in the first years: Es = −1.12, and two peaks are observed. When we truncate the first year of life, in the remaining cohort CVLS = 46.63%, i.e., the population is not homogeneous: As = –0.85, significant left-sided skewness; Es = –0.51, two peaks are observed. Truncation of individuals who died in the first 10 years of life leads to CVLS = 37.11% – the population is close to homogeneous, left-sided skewness did not change significantly (As = –0.91), whereas kurtosis decreased (Es = –0.08). Significant increase in mortality is observed only at an older age.
Aché Indians: after truncation of the first two years of life, CVLS in the cohort constitutes 60.46%, i.e., the sample is not homogeneous, mortality in the first years is high: As = −0.10, slight left-sided skewness; Es = −1.29, there are no peaks. After the truncation of the first ten years of life, CVLS = 54.54%, i.e., the cohort is still heterogeneous. We concluded that data truncation “according to Gavrilov” is effective for the study of human populations, although it does not always lead to CV decrease to 33% (as in other representatives of the order Primates).
For laboratory mice (Mus musculus) and rats (Rattus norvegicus), CVLS values in various lines (differing by LS95!) practically never exceeded 33%, which indicates homogeneity of their populations, probably due to a decrease in the level of background mortality and genetic diversity. The same applies to laboratory invertebrates (table, part D) and fish (guppies) (table, part A).
Summarizing the data on lifespan distribution in birds (table, part B), we note that in small (weight <1 kg) birds in the wild As varies from 0.29 to 1.4, and Es from –0.88 to 2.16 (see table and text), i.e., deviations from normality are not pronounced. CVLS ranges from 29.6 to 69.9%, indicating a significant contribution of background mortality to overall mortality.
This suggests that most representatives of this group are characterized by high heterogeneity in mortality as well as moderate and significant right-sided skewness. They are also heterogeneous in relation to kurtosis value – from an approximately uniform distribution to concentration of values near the mean. The lowest values for all three indicators are characteristic of the southern fulmar, which is knocked out of this row by all parameters, probably due to a long period of practically zero mortality (see also [54]). In case of large birds (swan) with lifespan up to 29 years in the wild and 70 in captivity [55], as well as birds with few enemies (sparrowhawk and southern fulmar), the CVLS ranges from 29.5 to 73.8%, skewness from 0.29 to 1.11, and kurtosis from –0.88 to 1.11, which hardly differs from the parameters of the group of small birds considered above. If we compare these data with the data for Rothschild’s mynah kept in captivity (in zoos), which is threatened with extinction and therefore special efforts were made to eliminate its background mortality, this bird basically fits the general series (CVLS = 66%, As = 0.19, Es = −1.17). In relation to the last two parameters, it is closer to the fulmar, while by weight and lifespan to swift. Captivity had little effect on its CVLS. In general, summarizing data on birds, we can say that birds are very heterogeneous in relation to all the discussed parameters.
The most inhomogeneous sample is characteristic of reptiles (table, part C) and of the Gopherus agassizii gopher: for the total cohort CVLS = 160.00%, As = 5.59, Es = 44.90 – an extremely high value (at such Es values, it can be assumed that neither CVLS nor the mean characterize the studied population, apparently despite the long lifespan and resistance to aging, the effect of child mortality is too great).
In the cohort resulting from the truncation of individuals who died in the first year of life, CVLS = 98.31 – high infant mortality was eliminated, As = 4.42, Es = 26.51. Truncation of the first 11 years of life resulted in CVLS = 56.42%. Although, after subtracting the first eleven years, CVLS dropped (due to elimination of child mortality and reduction of the general size), in the end it remained very high: As = 1.89, Es = 3.30 – these parameters decreased due to removal of the first years of life with high mortality values.
In all three cases, As > 0, i.e., there is a significant right-sided skewness. High mortality is observed only at early ages; later it becomes low and does not grow with age. Kurtosis is positive in all three cases, and peaked character is observed with respect to the normal distribution and concentration of values near the average. In further calculations, we found that to achieve homogeneity of the cohort in relation to lifespan (33%), no less than the first 25 years of life need to be truncated in case of tortoise. At earlier ages, tortoise lifespan depends more on background mortality. Perhaps this is the reason for the recent heated discussion on whether the tortoises and turtles are aging (or whether the probability of their death increases with age). Note: in 2011, the species Gopherus agassizii was divided into two [56].
It should be noted that although tortoises as well as reptiles in general were considered an “icon” of longevity not prone to aging [57, 58], recent studies have advocated the opposite point of view [38], although so far, this discussion has involved not the large tortoises with unlimited growth, but several small turtles considered to be non-aging despite the limited growth (marsh turtle, carolina box turtle, Blanding’s turtle, and painted turtle). In this regard, measuring the sustainability of mortality and the characteristics of lifespan distribution becomes even more important.
Johnstone’s crocodile (Crocodylus johnstoni): for the complete cohort, CVLS = 194.52%, i.e., the sample is extremely heterogeneous: As = 3.94, Es = 12.44. In a cohort without the first year of life, CVLS = 91.50%, As = 1.08, Es = 0.38, and heterogeneity is reduced by eliminating infant mortality. In a cohort without the first two years of life, CVLS is reduced to 60.38%, and without the first eleven years of life (“Jones truncation” till the age of puberty) CVLS = 34.18%. Skewness and kurtosis do not undergo any significant change.
Thus, truncating two years is enough to eliminate the effect of extremely high infant mortality, while truncating the years till the age of puberty makes the cohort virtually homogeneous. In all cases, there is a significant right-sided skewness, showing a high mortality rate at early age, which decreases in later years. The value of kurtosis for a full cohort is unacceptably high, and in other cases kurtosis is close to zero.
With the Lacerta vivipara lizard, for the full cohort CVLS = 69.28%, Es = 5.30 – high kurtosis coefficient due to high mortality in the first year. Truncation of the first year of life results in CVLS = 55.92%, Es = –0.29 – kurtosis is insignificant, but CVLS indicates preservation of population heterogeneity.
Coefficient of variation of lifespan (CVLS). Earlier [59], we concluded that identification of temporal scaling based on CVLS equality in compared cohorts allows us to distinguish first the quantitative differences in the dynamics of aging from qualitative ones.
Statistical description of the phenomenon will be incomplete if we confine ourselves to the parameters of the central tendency, i.e., mean values, mode, and median. In some cases, the values of the parameter are concentrated closely to the center, while in others there is considerable dispersion, although the average value may be the same.
Here is an example of this phenomenon: individual lifespan deviations (caused not by general conditions and causes, but by personal circumstances of peoples’ lives) of people that are in the same age range, and therefore probability of their death is by definition the same. Therefore, studying deviations of individual parameters from the average values and patterns of their distribution is of great interest for the biology of aging. This is important, first, for assessing the homogeneity of the population, which is characterized by a given average value, since the more homogeneous the population, the smaller its variation. Consequently, the smaller CVLS, the more qualitatively homogeneous is the population, and the more typical and objective is the average value characterizing it.
Calculated CVLS values indicate a greater lifespan variation in Swedes (37.11%) and Indians (54.54%) compared to Japanese females (16.15%), despite the longer lifespan in the latter. Thus, CVLS is an objective characteristic of the population as a whole, showing that the population of Japanese females as a whole is more homogeneous (for comparison, in Gavrilova et al., CVLS = 20.5% for American females aged over 10 years [1]). It is generally accepted that at CVLS exceeding 33%, the population is not homogeneous (in our case this means a significant contribution of background mortality).
At CVLS values exceeding 67%, it is generally assumed that the average does not characterize the population, i.e., the calculated average lifespan (and, consequently, the relative spread around it, i.e., CVLS) does not characterize the true state of the population. For example, if, when calculating mortality data for Indians, we consider all age intervals (i.e., also infant mortality), the average lifespan will be 27-30 years, which is clearly an irrelevant characteristic of human lifespan. Moreover, it is not recommended to apply CVLS (as well as the mean) also at excessively high kurtosis, as the probability of artifacts becomes high; it is necessary to ensure that after truncation the kurtosis coefficient would be reduced to acceptable values (no more than 3) (see above, values for total reptile cohorts).
It has already been noted that “truncated” data sets are used to overcome this problem, i.e., lifespan distribution parameters are calculated in the cohort, starting at the age of 10 (which is considered to be the age when age-related mortality starts to increase [1]), or at 12-15 years – the age of puberty [2]. In addition to that, Jones also uses truncation of late age intervals to 95% mortality. It should be noted that in case of this truncation, CVLS declines well below the threshold value of 33%, reaching 15-20%. CVLS characteristic of twins (i.e., with near-zero difference in the genetic component effect) has a similar value [60].
In addition, the method of data truncation (removing a certain number of years from consideration), being convenient for human populations, is difficult to apply to other representatives of the animal world, since many of them, even the long-lived swans and southern fulmars, have no pronounced postnatal peak in the first year of life, or the age of puberty is reached in the first year of life, not allowing, according to Jones’s method, to cut off the first few intervals. Checking the prevalence of this phenomenon, we studied the CVLS values as well as the coefficients of skewness and kurtosis in various representatives of the animal kingdom using the data provided by the Institute for Demographic Research [2]. We found that, unlike humans and laboratory animals, most of the examined species are characterized by heterogeneous parameters due to the significant effect of background mortality, as well as the nonmonotonicity of total mortality in the wild, especially at the earliest ages. One way to account for this effect is to “truncate” data (removing a certain number of years from consideration).
To reveal the effect of this procedure, we proposed a new indicator, the stability coefficient of mortality dynamics (hereinafter – stability coefficient), indicating how quickly during “truncation” CVLS will drop to values characteristic of a relatively homogeneous population (33%).
Therefore, we decided to determine how quickly the truncation of the initial age intervals will make lifespan distribution homogeneous, i.e., will reduce CVLS to 33%. At the initial stages, contribution of the age component to total mortality is low; since there are no individuals that have aged (even progerias do not appear instantaneously). CVLS reduction to 33% (T1) excludes a strong effect of background mortality on the lifespan distribution curve.
However, it is also possible to solve the opposite task – to test the stability margin of mortality dynamics, by truncating intervals from the opposite side, i.e., removing intervals with the most aged individuals. This identifies the “power” of the age component. In this case, after CVLS drops to 33% (T2), the age component has practically no effect on the parameters of lifespan distribution. Thus, by deleting several final intervals, Jones greatly reduces the contribution of the age-dependent mortality component.
Thus, T1 is the age when CVLS drops to 33% after the sequential truncation of initial intervals. T2 is the age when CVLS drops to 33% after sequential truncation of the final intervals. We assume that the ratio of the described ages (T2 and T1), CVLS33%, will be higher in species that are “resistant” to aging (long-lived or slowly aging species), and will be lower in rapidly aging and/or short-lived species. Thus, for crocodile this parameter was 17.5, for orca – 11, swan – 5, marmot – 4, vole – 3.75, great tit – 3, lizard – 2.75, sparrowhawk – 2.5, guppy – 2,25, swift – 1.75, and collared flycatcher – 1.5. It reaches its greatest value in humans (102 in Japanese females), as well as in southern fulmar (35), chimpanzee – 44, tortoise – 26, and baboon – 22.
These results support Cohen’s view that aging is very different in long-lived and short-lived species, and that in some cases long-lived animals (including birds and bats) might be better models for studying human aging than laboratory animals with short lifespan, despite a closer phylogenetic relationship between humans and, e.g., laboratory mice and rats [61].
Finally, when speaking about non-aging animals, it is impossible to not omit mention of the naked mole rat, Heterocephalus glaber. Mortality of naked mole rats is very low and depends little on age; as a result, their lifespan is over 30 years, which makes them very different from other rodents [50]. V. P. Skulachev suggested that the longevity of highly social mammals, such as naked mole rats and humans, is primarily due to neoteny (prolongation of youth) [50]. In both of these species, aging cannot function as a mechanism stimulating natural selection, since the pressure of selection is greatly reduced: in naked mole rats due to the social structure where only one female is involved in reproduction, and in humans due to technological progress that has replaced slow biological evolution.
Data on the survival of the naked mole rats were not used by Jones et al. because of inadequate, in their opinion, data on mortality in the first year. Nevertheless, based on the shape of the survival curve, naked mole rats should be attributed to the group of non-aging animals (group I) [42]. In our research, we calculated the stability coefficient for the naked mole rat, based on the data provided by Buffenstein [62, 63]. This coefficient was ~12, which is less than in primates, and is comparable to that of crocodile and orca. It should be noted that this value may be somewhat underestimated because the available survival data for the naked mole rat embrace only the period to 24 years, whereas its lifespan can be at least 1.5 times longer.
The longer is lifespan and the slower is aging, the higher is the proposed parameter, the coefficient of stability. In particular, it avoids such mistakes as the attribution of two exceptionally slowly aging species (tortoise and southern fulmar) with radically different dynamics of aging, respectively, to the non-aging (tortoise) and strongly aging species (southern fulmar) [2]. In essence, the ratio of the coefficient of stability to the maximum lifespan is the indicator of “instant stability of life”: the smaller it is, the higher the probability of death of an individual of the given species at any moment in the life cycle.
We assume that the coefficient of stability reflects the “stability of the dynamics” of aging (i.e., it plays the same role as the “compensation effect” [34, 64] and the Strehler–Mildvan correlation in its various modifications [35, 65]), connecting the initial level (preexponential factor) and the growth rate (exponent index) of mortality in the Gompertz equation.
The approach of the Gavrilovs has a different theoretical basis that does not intersect with the question of the shape of the survival curves and their change. They put forward the idea of the presence of a characteristic level of variability inherent in ontogenetic event onset time [1]. For example, CVLS = 20% on the average LS of 80 years, obtained for Caucasian women in the developed countries (one of the most prosperous human populations), suggests that about two-thirds of them will die in the 64-96 age range.
The fact that we do not know the degree of genetic heterogeneity of the samples presents another difficulty in implementing the proposed approach. If the sample is characterized by a large variability in lifespan-affecting genes, then CVLS can be high even if lifespan is very rigidly regulated by the genes of each individual. Hence, it seems interesting to study, using the approach proposed in this article (with truncation of young ages, until the CVLS decreases to 33%), long-lived laboratory animals whose background mortality is close to zero.
In addition, it is important to understand what lifespan distribution we expect to see under any given assumptions. For example, let us consider the situation when aging is completely absent, and probability of the organism’s death is independent of its age. In other words, death is a random event caused by some external factors and is independent of the state of the organism. In this case, the survival curve will have exponential form, and lifespan distribution will not be normal (for example, in the first year, 20% of the cohort died, in the second year, 20% of the remainder, etc. – this will be a sharply asymmetric distribution with right skewness, where the mode will be much to the left of the mean). Thus, right skewness may indicate stochastic mortality and a low contribution of genes to determination of lifespan.
Symmetrical lifespan distribution is expected when lifespan is strictly controlled genetically, and some random scatter is observed around the “ideal”, genetically programmed, lifespan. The survival curve will then look like that of Japanese and Swedish females: very low mortality for a long time, and then all relatively quickly die. Thus, we assume that the degree of right-sided skewness in lifespan distribution is positively correlated with the degree of stochasticity in lifespan determination and negatively with gene contribution to this determination. Left-sided skewness probably means that the death of young individuals can sometimes be caused by tragic accidents (or, perhaps, a particularly unfortunate genotype), but in mature individuals the role of chance is minimized, and genetic lifespan determination comes to the fore. In other words, the larger part of the population (except for those who died in youth for one reason or another) is limited by genetically determined maximum lifespan (maximum for concrete living conditions, of course). This can be true for both orcas and modern people from developed countries.
It should always be taken into account that variability of any character, including lifespan, consists of two components: hereditary (genetic) and non-hereditary, which can be divided into environmental or modificational (according to Darwin, it is determinate variation) and stochastic. Most importantly, the ratio of the contribution of genes and (environmental + stochastics) to variability of any given trait is not a constant, but depends on the circumstances. For example, in case of lifespan this ratio depends on lifestyle, sociality, security, etc.
If a population is placed in some constant favorable conditions and these conditions are leveled for all individuals, then environmental variability will be reduced to a minimum, and almost the entire remaining variability in the population will be due to the genetic component. Apparently, this is observed in Japanese and Swedish females. They live in protected standard conditions created by civilization. Accidental mortality is almost excluded under these conditions, especially after the individuals with defective genotypes had already been eliminated. Therefore, all individuals live as long as it is “recorded” in their genes, with a margin of small remaining non-hereditary variability.
The main problems we face when studying survival curves are the presence of too many unknowns: for example, we do not know the level of genetic variability (heterogeneity) in the samples and the mechanisms of gene–environment interactions. It is obvious that the same allele can reduce lifespan when conditions are unfavorable, but it does not affect lifespan in ideal conditions. Genes that affect the lifespan of Indians may have no effect of lifespan of Japanese. For example, one can imagine a gene that helps to endure starvation or survive after a bite of a poisonous snake. Alternatively, a gene that affects the rate of deterioration of joints (or heart, or other important organs) involved in heavy physical work. In a society with no hard physical labor, this gene does not affect aging, but in a primitive society its impact is very strong. Thus, habitat conditions can radically change the system of lifespan genetic determination in the same species.
Earlier, V. P. Skulachev suggested that not all age-related changes in an organism, as well as changes in environmental conditions, will immediately affect age-related increase in death probability (oral communication). Thus, they can affect the shape of the survival curve in different ways (A. V. Khalyavkin refers to this as the modal environmental pressure [35]), leading to an increase in mortality not in the original, but in subsequent age intervals, depending on the overall “stability” of the organism (the conditions of its existence, etc.). The coefficient of stability of mortality dynamics depends on this type of mortality. Thus, we assume that the greater the value of the T2/T1 ratio, the more time will pass from the appearance of any damages to organisms to their manifestation on the Gompertz curve (age-related increase in death probability) and the more it will be “guaranteed” that the negative effect will be manifested not via accidental mortality (its background component), but through the age-dependent component. Otherwise, it will be difficult to distinguish between the slow growth of mortality with age (slow aging) and the absence of such growth due to other reasons (constant predator pressure). We have already discussed the result of such a misinterpretation – attribution of rapidly dying animals (e.g. great tits) to non-aging species (see also [42]), when analyzing classification of animals based on the pace and shape of aging (see, for example, [2, 66, 67]). Direct comparison of the death rate in the final interval with the average parameter for the entire studied period in different populations sometimes leads to a different conclusion than comparison of the relative variation parameters.
Earlier, we discussed the conclusions drawn in previous studies, that CVLS reflects also the degree of the programmed character of aging [1], as well as its rate and mechanism [5, 37, 68]. We assume that CVLS “dynamics” (degree of change) after the removal of initial and final age intervals can serve as an indicator of the “stability” of population mortality and, consequently, the organism’s ability to resist it. Depending on the homogeneity of the population, variability of characteristics may be large or small [69-73]. Therefore, there is a need to measure lifespan variations with respect to the mean value (CVLS), both for studying the dynamics of mortality in the wild and in the laboratory, and for studying the efficacy of various drugs and geroprotectors that increase not only the mean and median lifespan, but also the duration of a healthy life (healthspan).
Acknowledgments
We are very grateful to V. P. Skulachev for the original idea, as well as for invaluable help, advice, and comments related to this article.
We are also grateful to K. G. Lyamzayev, I. D. Kan, S. V. Kruskop, and L. S. Yaguzhinsky for valuable advice and comments.
This work was supported by the Russian Science Foundation (project 14-50-00029).
REFERENCES
1.Gavrilova, N. S., Gavrilov, L. A., Severin, F. F.,
and Skulachev, V. P. (2012) Testing predictions of the programmed and
stochastic theories of aging: comparison of variation in age at death,
menopause, and sexual maturation, Biochemistry (Moscow),
77, 754-760.
2.Jones, O. R., Scheuerlein, A., Salguero-Gomez, R.,
Camarda, C. G., Schaible, R., Casper, B. B., Dahlgren, J. P., Ehrlen,
J., Garcia, M. B., Menges, E. S., Quintana-Ascencio, P. F., Caswell,
H., Baudisch, A., and Vaupel, J. W. (2014) Diversity of ageing across
the tree of life, Nature, 505, 169-173.
3.Vaupel, J. W., Carey, J. R., Christensen, K.,
Johnson, T. E., Yashin, A. I., Holm, N. V., Iachine, I. A., Kannisto,
V., Khazaeli, A. A., Liedo, P., Longo, V. D., Zeng, Y., Manton, K. G.,
and Curtsinger, J. W. (1998) Biodemographic trajectories of longevity,
Science, 280, 855-860.
4.Baudisch, A. (2008) Inevitable Aging?
Contributions to Evolutionary-Demographic Theory,
Springer-Verlag, Berlin-Heidelberg.
5.Skulachev, M. V., and Skulachev, V. P. (2014) New
data on programmed aging – slow phenoptosis, Biochemistry
(Moscow), 79, 977-993.
6.Markov, A. V. (2012) Can kin selection facilitate
the evolution of the genetic program of senescence? Biochemistry
(Moscow), 77, 733-741.
7.Hyams, Y., Paz, G., Rabinowitz, C., and Rinkevich,
B. (2017) Insights into the unique torpor of Botrylloides
leachii, a colonial urochordate, Dev. Biol., 428,
101-117.
8.Fisher, R. A. (1930) The Genetical Theory of
Natural Selection, Clarendon Press, Oxford.
9.Medawar, P. B. (1952) An Unsolved Problem of
Biology, H. K. Lewis, London.
10.Hamilton, W. D. (1966) The moulding of senescence
by natural selection, J. Theor. Biol., 12, 12-45.
11.Nusbaum, N. J. (1996) What good is it to get old?
Med. Hypotheses, 47, 77-79.
12.Brent, L. J., Franks, D. W., Foster, E. A.,
Balcomb, K. C., Cant, M. A., and Croft, D. P. (2015) Ecological
knowledge, leadership, and the evolution of menopause in killer whales,
Curr. Biol., 25, 746-750.
13.Kirkwood, T. B. L. (2010) Systems biology of
ageing and longevity, Phil. Trans. R. Soc. B., 366,
64-70.
14.Williams, G. C. (1957) Pleiotropy, natural
selection and the evolution of senescence, Evolution, 11,
398-411.
15.Vijg, J., and Suh, Y. (2005) Genetics of
longevity and aging, Annu. Rev. Med., 56, 193-212.
16.Campisi, J. (2005) Aging, tumor suppression and
cancer: high wire-act! Mech. Ageing Dev., 126, 51-58.
17.Liu, J. J., Prescott, J., Giovannucci, E.,
Hankinson, S. E., Rosner, B., Han, J., and De Vivo, I. (2013) Plasma
vitamin D biomarkers and leukocyte telomere length, Am. J.
Epidemiol., 177, 1411-1417.
18.Zhu, Y., Tchkonia, T., Pirtskhalava, T., Gower,
A. C., Ding, H., Giorgadze, N., Palmer, A. K., Ikeno, Y., Hubbard, G.
B., Lenburg, M., O'Hara, S. P., LaRusso, N. F., Miller, J. D., Roos, C.
M., Verzosa, G. C., LeBrasseur, N. K., Wren, J. D., Farr, J. N.,
Khosla, S., Stout, M. B., McGowan, S. J., Fuhrmann-Stroissnigg, H.,
Gurkar, A. U., Zhao, J., Colangelo, D., Dorronsoro, A., Ling, Y. Y.,
Barghouthy, A. S., Navarro, D. C., Sano, T., Robbins, P. D.,
Niedernhofer, L. J., and Kirkland, J. L. (2015) The Achilles’
heel of senescent cells: from transcriptome to senolytic drugs,
Aging Cell, 14, 644-658.
19.Skulachev, V. P. (1997) Aging is a specific
biological function rather than the result of a disorder in complex
living systems: biochemical evidence in support of Weismann’s
hypothesis, Biochemistry (Moscow), 62, 1191-1195.
20.Skulachev, V. P. (1999) Phenoptosis: programmed
death of an organism? Biochemistry (Moscow), 64,
1418-1426.
21.Weismann, A. (1889) Essays upon Heredity and
Kindred Biological Problems, Oxford, Clarendon Press.
22.Guarente, L., and Kenyon, C. (2000) Genetic
pathways that regulate ageing in model organisms, Nature,
408, 255-262.
23.Longo, V. D., Mitteldorf, J., and Skulachev, V.
P. (2005) Programmed and altruistic ageing, Nature Rev. Genet.,
6, 866-872.
24.Fushan, A. A., Turanov, A. A., Lee, S. G., Kim,
E. B., Lobanov, A. V., Yim, S. H., Buffenstein, R., Lee, S. R., Chang,
K. T., Rhee, H., Kim, J. S., Yang, K. S., and Gladyshev, V. N. (2015)
Gene expression defines natural changes in mammalian lifespan, Aging
Cell, 14, 352-365.
25.Ma, S., and Gladyshev, V. N. (2017) Molecular
signatures of longevity: insights from cross-species comparative
studies, Semin. Cell. Dev. Biol., pii: S1084-9521.
26.Ashapkin, V. V., Kutueva, L. I., and Vanyushin,
B. F. (2015) Aging epigenetics: accumulation of errors or realization
of a specific program? Biochemistry (Moscow), 80,
1406-1417.
27.Stegeman, R., and Weake, V. M. (2017)
Transcriptional signatures of aging, J. Mol. Biol., 429,
2427-2437.
28.Austad, S. N. (1993) Retarded senescence in an
insular population of opossums, J. Zool. (Lond.), 229,
695-708.
29.Skulachev, M. V., Severin, F. F., and Skulachev,
V. P. (2015) Aging as an evolvability-increasing program which can be
switched off by organism to mobilize additional resources for survival,
Curr. Aging Sci., 8, 95-109.
30.Hughes, B. G., and Hekimi, S. (2017) Many
possible maximum lifespan trajectories, Nature, 546,
8-9.
31.Gompertz, B. (1825) On the nature of the function
expressive of the law of human mortality and on a new mode of
determining life contingencies, Philos. Trans. R. Soc. L. A.,
115, 513-585.
32.Deevey, E. S. (1947) Life tables for natural
populations of animals, Q. Rev. Biol., 22, 283-314.
33.Finch, C. E. (1990) Longevity, Senescence and
the Genome, University Chicago Press, Chicago.
34.Gavrilov, L. A., and Gavrilova, N. S. (1991)
The Biology of Life Span: A Quantitative Approach, Harwood
Academic Publisher, N. Y.
35.Khalyavkin, A. V. (2001) Influence of environment
on the mortality pattern of potentially non-senescent organisms.
General approach and comparison with real populations, Adv.
Gerontol., 7, 46-49.
36.Ricklefs, R. E. (2010) Life-history connections
to rates of aging in terrestrial vertebrates, Proc. Natl. Acad. Sci.
USA, 107, 10314-10319.
37.Stroustrup, N., Anthony, W. E., Nash, Z. M.,
Gowda, V., Gomez, A., Lopez-Moyado, I. F., Apfeld, J., and Fontana, W.
(2016) The temporal scaling of Caenorhabditis elegans
ageing, Nature, 530, 103-107.
38.Warner, D. A., Miller, D. A., Bronikowski, A. M.,
and Janzen, F. J. (2016) Decades of field data reveal that turtles
senesce in the wild, Proc. Natl. Acad. Sci. USA, 113,
6502-6507.
39.Mitnitski, A., Howlett, S. E., and Rockwood, K.
(2017) Heterogeneity of human aging and its assessment, J. Gerontol.
A Biol. Sci. Med. Sci., 72, 877-884.
40.Baudisch, A., and Vaupel, J. (2010) Senescence
vs. sustenance: evolutionary-demographic models of aging, Demogr.
Res., 23, 655-668.
41.Mitnitski, A., Song, X., and Rockwood, K. (2013)
Assessing biological aging: the origin of deficit accumulation,
Biogerontology, 14, 709-717.
42.Shilovsky, G. A., Putyatina, T. S., Markov, A.
V., and Skulachev, V. P. (2015) Contribution of quantitative methods of
estimating mortality dynamics to explaining mechanisms of aging,
Biochemistry (Moscow), 80, 1547-1559.
43.Akif’ev, A. P., and Potapenko, A. I. (2001)
Nuclear genetic material as an initial substrate of aging in animals,
Russ. J. Genet., 37, 1213-1223.
44.Blagosklonny, M. V. (2007) Program-like aging and
mitochondria: instead of random damage by free radicals, J. Cell.
Biochem., 102, 1389-1399.
45.Goldsmith, T. C. (2008) Aging, evolvability, and
the individual benefit requirement; medical implications of aging
theory controversies, J. Theor. Biol., 252, 764-768.
46.Libertini, G. (2012) Phenoptosis, another
specialized neologism, or the mark of a widespread revolution?
Biochemistry (Moscow), 77, 795-798.
47.Khokhlov, A. N. (2010) Does aging need an own
program or the existing development program is more than enough,
Russ. J. Gen. Chem., 80, 1507-1513.
48.Shilovsky, G. A., Khokhlov, A. N., and Shram, S.
I. (2013) The protein poly(ADP-ribosyl)ation system: its role in genome
stability and lifespan determination, Biochemistry (Moscow),
78, 433-444.
49.Khalyavkin, A. V. (2013) Phenoptosis as
genetically determined aging influenced by signals from the
environment, Biochemistry (Moscow), 78, 1001-1005.
50.Skulachev, V. P., Holtze, S., Vyssokikh, M. Y.,
Bakeeva, L. E., Skulachev, M. V., Markov, A. V., Hildebrandt, T. B.,
and Sadovnichii, V. A. (2017) Neoteny, prolongation of youth: from
naked mole rats to “naked apes” (humans), Physiol.
Rev., 97, 699-720.
51.Timofeeff-Ressovsky, N. W. (1927) Studies on the
phenotype manifestation of hereditary factors. I. On the phenotypic
manifestation of the genovariation radius incompletus in Drosophila
funebris, Genetics, 12, 128-198.
52.Comfort, A. (1979) The Biology of
Senescence, Churchill Livingstone, Edinburgh-London.
53.Carey, J. R., and Judge, D. S. (2001)
Odense Monographs on Population Aging, Ser. 8, Odense
University Press, Odense, Denmark.
54.Bowles, J. T. (1998) The evolution of aging: a
new approach to an old problem of biology, Med. Hypotheses,
51, 179-221.
55.Terres, J. (1980) The Audubon Society
Encyclopedia of North American Birds, Knopf, New York.
56.Murphy, R., Berry, K., Edwards, T., Leviton, A.,
Lathrop, A., and Riedle, J. (2011) The dazed and confused identity of
Agassiz’s land tortoise, Gopherus agassizii (Testudines:
Testudinidae) with the description of a new species and its
consequences for conservation, ZooKeys, 113, 39-71.
57.Miller, J. K. (2001) Escaping senescence:
demographic data from the three-toed box turtle (Terrapene carolina
triunguis), Exp. Gerontol., 36, 829-832.
58.Congdon, J. D., Nagle, R. D., Kinney, O. M., van
Loben Sels, R. C., Quinter, T., and Tinkle, D. W. (2003) Testing
hypotheses of aging in long-lived painted turtles (Chrysemys
picta), Exp. Gerontol., 38, 765-772.
59.Shilovsky, G. A., Putyatina, T. S., Lysenkov, S.
N., Ashapkin, V. V., Luchkina, O. S., Markov, A. V., and Skulachev, V.
P. (2016) Is it possible to prove the existence of an aging program by
quantitative analysis of mortality dynamics? Biochemistry
(Moscow), 81, 1461-1476.
60.Finch, C. E., and Tanzi, R. E. (1997) Genetics of
aging, Science, 278, 407-411.
61.Cohen, A. A. (2017) Aging across the tree of
life: the importance of a comparative perspective for the use of animal
models in aging, Biochim. Biophys. Acta, pii: S0925-4439.
62.Buffenstein, R. (2005) The naked mole-rat: a new
long-living model for human aging research, J. Gerontol. A Biol.
Sci. Med. Sci., 60, 1369-1377.
63.Buffenstein, R. (2008) Negligible senescence in
the longest living rodent, the naked mole-rat: insights from a
successfully aging species, J. Comp. Physiol. B, 178,
439-445.
64.Gavrilov, L. A., Gavrilova, N. S., and
Yaguzhinsky, L. S. (1978) The main directions of the aging and death of
animals from the point of view of reliability theory, J. Gen.
Biol., 39, 734-742.
65.Tarkhov, A. E., Menshikov, L. I., and Fedichev,
P. O. (2017) Strehler–Mildvan correlation is a degenerate
manifold of Gompertz fit, J. Theor. Biol., 416,
180-189.
66.Jones, O. R., Gaillard, J. M., Tuljapurkar, S.,
Alho, J. S., Armitage, K. B., Becker, P. H., Bize, P., Brommer, J.,
Charmantier, A., Charpentier, M., Clutton-Brock, T., Dobson, F. S.,
Festa-Bianchet, M., Gustafsson, L., Jensen, H., Jones, C. G., Lillandt,
B. G., McCleery, R., Merilä, J., Neuhaus, P., Nicoll, M. A.,
Norris, K., Oli, M. K., Pemberton, J., Pietiäinen, H., Ringsby, T.
H., Roulin, A., Saether, B. E., Setchell, J. M., Sheldon, B. C.,
Thompson, P. M., Weimerskirch, H., Jean Wickings, E., and Coulson, T.
(2008) Senescence rates are determined by ranking on the fast-slow
life-history continuum, Ecol. Lett., 11, 664-673.
67.Baudisch, A. (2011) The pace and shape of ageing,
Methods Ecol. Evol., 2, 375-382.
68.Markov, A. V., Naimark, E. B., and Yakovleva, E.
U. (2016) Temporal scaling of age-dependent mortality: dynamics of
aging in Caenorhabditis elegans is easy to speed up or slow
down, but its overall trajectory is stable, Biochemistry
(Moscow), 81, 906-911.
69.Nussey, D. H., Froy, H., Lemaitre, J. F.,
Gaillard, J. M., and Austad, S. N. (2013) Senescence in natural
populations of animals: widespread evidence and its implications for
bio-gerontology, Ageing Res. Rev., 12, 214-225.
70.Lamb, M. J. (1977) Biology of Aging, John
Wiley and Sons, New York.
71.Voituron, Y., De Fraipont, M., Issartel, J.,
Guillaume, O., and Clobert, J. (2011) Extreme lifespan of the human
fish (Proteus anguinus): a challenge for ageing mechanisms,
Biol. Lett., 7, 105-107.
72.Anisimov, V. N. (2008) Molecular and
Physiological Mechanisms of Aging [in Russian], Nauka, St.
Petersburg.
73.Myl’nikov, S. V. (2011) Towards the
estimation of survival curves parameters and geroprotectors
classification, Adv. Gerontol., 24, 563-569.