REVIEW: Antiaggregation Activity of Chaperones and Its Quantification
B. I. Kurganov
Bach Institute of Biochemistry, Russian Academy of Sciences, Leninsky pr. 33, 119071 Moscow, Russia; E-mail: kurganov@inbi.ras.ru
Received April 12, 2013
Methods for the quantitative estimation of the antiaggregation activity of protein chaperones (first of all, small heat shock proteins) and chemical chaperones including amino acids, carbohydrates, polyamines, and cyclodextrins are discussed. Based on analysis of the plots of light scattering intensity or apparent optical absorption versus time, formulas for calculation of initial rate of aggregation of protein substrate and lag period on kinetic curves of aggregation were derived. Possible determination of the stoichiometry of chaperone–protein substrate complex from the dependence of the initial rate of aggregation on the ratio of protein chaperone/protein substrate concentrations is discussed. To characterize efficiency of the protective action of chemical chaperones, the [L]0.5 value can be used ([L]0.5 is the concentration of a chemical chaperone at which twofold decrease in the initial rate of aggregation occurs). Methods for quantitative estimation of the combined protective action of chaperones are discussed.
KEY WORDS: small heat shock proteins, chemical chaperones, protein aggregation, chaperone-like activity, cyclodextrinsDOI: 10.1134/S0006297913130129
Abbreviations: GAPDH, glycerlaldehyde-3-phosphate dehydrogenase; HP-β-CD, 2-hydroxypropyl-β-cyclodextrin; Phb, glycogen phosphorylase b; sHsp, small heat shock protein.
The spacial structure of proteins is rather labile and depends on
external conditions. Stress conditions can cause formation of unfolded
protein forms that exhibit enhanced tendency to aggregation. During
biosynthesis of proteins in cells, folding of the newly synthesized
polypeptide chains can be accompanied by formation of non-native
protein forms with a tendency to aggregate [1-5]. On the cell level, damages related with
aggregation of proteins are rather limited and are repaired by the
protein quality control system including chaperones and proteases [6]. The heat shock proteins belonging to Hsp60 (GroEL
in bacteria) and Hsp70 (DnaK in bacteria) families play the main role
in protein folding. Using the energy of ATP hydrolysis, Hsp60 and Hsp70
provide for proper folding of newly synthesized polypeptide chains and
correction of the structure of improperly folded proteins [6-8].
The family of small heat shock proteins (sHsp) has a special place among the heat shock proteins; the main function of sHsp is suppression of aggregation of non-native protein forms. Representatives of this family are found in almost all living organisms. The low molecular mass of monomers (from 12 to 43 kDa) and tendency to formation of large oligomers with molecular masses up to 1000 kDa are typical of this protein family [9-22]. The presence of a conservative α-crystallin domain in the structure of sHsp is also typical of this protein family. sHsp cannot provide folding of the polypeptide chain; however, they form complexes with non-native protein forms and can transfer the latter either to ATP-dependent chaperones or proteasomes, where proteolytic degradation of the unfolded proteins occurs [23-27]. sHsp oligomers are rather mobile structures: a high rate of subunit exchange between sHsp oligomers has been experimentally demonstrated [28-34].
sHsp–protein substrate complexes are characterized by a high degree of polydispersity [35, 36]. This hinders study of the structures of the complexes. Thus arising difficulties were overcome by using high-resolution mass spectrometry [37]: for example, studying the interaction of Hsp18.1 with luciferase denatured at 42°C by tandem mass spectrometry, more than 300 Hsp–protein substrate complexes with various stoichiometry were detected [38]. Such complexes are not static structures and are able to include additional amounts of protein substrate [35, 36, 38]. Moreover, Hsp subunits are capable of exchange with free Hsp oligomers and sHsp–protein substrate complexes. In contrast, protein substrate in the composition of a complex seems to be unable for transfer from one complex to another [36].
Not only small heat shock proteins, but also heat shock proteins built of larger subunits possess antiaggregation activity. For example, the antiaggregation activity of GroEL, a representative of the heat shock protein family Hsp60, was demonstrated in [39-46]. The GroEL molecule has the form of an empty cylinder composed of 14 identical subunits of molecular mass 57 kDa. Subunits, constituents of the molecule, form two seven-membered rings adjacent to one another [47]. According to present views, folding of the non-native protein forms occurs in the ring cavity of the GroEL molecule with participation of co-chaperonin GroES, which acts as a lid; the process of folding includes hydrolysis of ATP [48-50].
An alternative mechanism of the chaperone activity of GroEL was suggested by Marchenkov and Semisotnov [51]: folding of the polypeptide chain occurs in solution, which is outside a complex with chaperonin, whereas chaperonin binds the non-native protein forms, thus decreasing their probable aggregation.
The heat shock protein Hsp90 also exhibits antiaggregation activity; the protein participates in folding of polypeptide chains and in protein degradation. The Hsp90 molecule is a dimer consisting of identical subunits with molecular mass of 90 kDa [52-57].
Numerous studies indicate that osmolytes stabilize protein structure and decrease the rate of protein unfolding by denaturing action [58-64]. Various chemical compounds such as amino acids (proline, alanine, glutamic acid, and others), trimethylamines (trimethylamine N-oxide, betaine, and others), and carbohydrates (glycerol, trehalose, sorbitol, mannitol, and others) are examples of such osmolytes. In experiments on protein refolding, it has been demonstrated that osmolytes increase the yield of native protein, i.e. they act as molecular chaperones. That is why osmolytes are called “chemical chaperones” [65-69]. The chaperone function of osmolytes is rationalized by their ability to suppress aggregation of the unfolded protein forms by interaction with hydrophobic sites on the surface of the protein molecules. The antiaggregation activity of osmolytes is well studied using test systems based on aggregation of protein substrates [70-76].
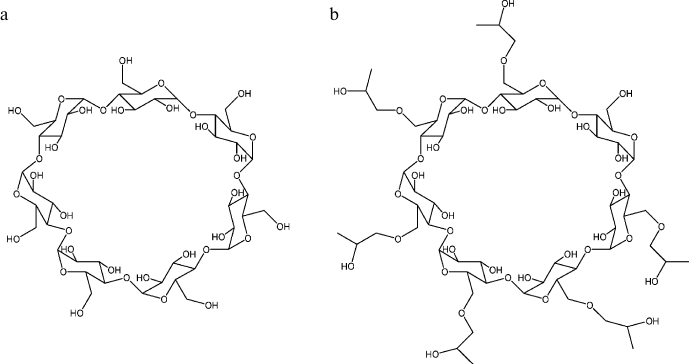
Cyclodextrins, which are cyclic oligomers of glucose [77-84], are also natural agents exhibiting antiaggregation activity. Cyclodextrins are composed of D-(+)-glucopyranose residues combined in macrocycles by α-D-1,4-glycosidic bonds. The structure of a β-cyclodextrin molecule composed of seven glucopyranose units is presented in Fig. 1a. The solubility of β-cyclodextrin in water is relatively low and can be increased by its chemical modification. The structure of 2-hydroxypropyl-β-cyclodextrin (HP-β-CD), one of the β-cyclodextrin derivatives with increased solubility, is presented in Fig. 1b. All the hydroxyl groups in cyclodextrins are on the outer surface of the molecule. That is why the inner cavity of cyclodextrins is hydrophobic and is able to form inclusion complexes with other organic and inorganic molecules in aqueous solutions. The antiaggregation properties of cyclodextrins are rationalized by their ability to form inclusion complexes with the exposed aromatic side groups of unfolded polypeptide chains; as a result, aggregation of the polypeptide is blocked.
Fig. 1. Structures of β-cyclodextrin (a) and 2-hydroxypropyl-β-cyclodextrin (b). The cavity of the cyclodextrin molecule is ~0.7 nm in diameter and ~0.8 nm in depth.
Agents possessing chaperone-like (antiaggregation) activity are applied in biotechnology and medicine. To obtain compounds exhibiting high efficiency as protective agents, researchers should have available methods for rigorous quantification of the antiaggregation activity of the studied compounds.
ESTIMATION OF INITIAL RATE OF PROTEIN AGGREGATION
To characterize the antiaggregation activity of a chaperone, we should estimate the initial rate of aggregation of the model protein substrate and compare this rate with the corresponding rate in the absence of the chaperone. Protein aggregates scatter light more than the non-aggregated protein molecules. That is why the simplest method for estimation of the initial rate of aggregation is measuring the increased light scattering intensity (I) or apparent optical absorption (A) in a wavelength area where optical absorption of the protein is absent. Time-dependent acceleration of aggregation is observed at the early stages; this is supposed to be caused by the nucleation stage. To characterize the initial stage of aggregation, we suggested using the quadratic time dependence for description of the initial portions of aggregation kinetic curves [85]:
or
where I0 and A0 are the initial values of light scattering intensity and apparent optical absorption, respectively, t is time, and t0 is lag period on the kinetic curve (time point when increase in light scattering intensity or apparent optical absorption begins). The constant Kagg can be considered as a measure of the initial rate of aggregation. Analysis demonstrates that the quadratic dependence should adequately describe aggregation including the nucleation stage [85, 86].
We demonstrated applicability of Eq. (1) for description of the initial portions of aggregation kinetic curves for thermal aggregation of glycogen phosphorylase b (Phb, EC 2.4.1.1) [46, 85, 87, 88], glycerlaldehyde-3-phosphate dehydrogenase (GAPDH, EC 1.2.1.12) [84, 89, 90], and creatine kinase (EC 2.7.3.2) [83] from rabbit skeletal muscles and dithiothreitol-induced aggregation of α-lactalbumin [91] and insulin [92].
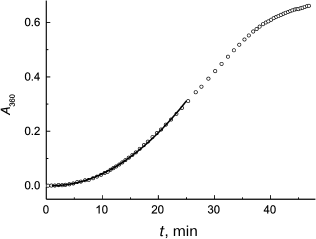
Figure 2 demonstrates the applicability of Eq. (2) for description of the initial portion of the aggregation kinetic curve of S1 myosin heads (0.5 mg/ml) studied in [93]. Parameters of Eq. (2) were found to be as follows: Kagg = (5.41 ± 0.04)·10–4 absorption units × min–2 and t0 = 1.0 ± 0.1 min (43°C). It should be mentioned that one of the advantages of the test system based on aggregation of S1 myosin heads is the possibility of studying antiaggregation activity of chaperones at temperatures close to physiological ones.
Fig. 2. Application of the Kagg parameter for characterization of the initial rate of aggregation. The time dependence of the apparent optical absorption at 360 nm (A360) for aggregation of S1 myosin heads (0.5 mg/ml) is plotted for the data from [93]. Conditions: 43°C, 30 mM Hepes, pH 7.3, containing 1 mM MgCl2 and 100 mM KCl. Circles are experimental data. Solid line is plotted using Eq. (2) at Kagg = 5.41·10–4 absorption units × min–2 and t0 = 1 min.
Equations (1) and (2) are practically valuable, because firstly, addition of chaperone usually results in increase in the lag period on aggregation kinetic curves, and using Eqs. (1) and (2) we can reliably determine change in the lag period duration. It should be noted that it is practically impossible to determine the lag period on kinetic curves visually. Second, determination of the Kagg parameter allows quantification of the antiaggregation activity of the chaperone.
Let us consider various modifications of Eqs. (1) and (2). First, we can enlarge time interval used for calculation of the t0 and Kagg parameters if these equations are modified as follows:
or
where K is a constant accounting for deviation from quadratic dependence. This is important that at t → t0 Eqs. (3) and (4) are transformed in Eqs. (1) and (2), respectively.
Second, it should be taken into account that in some cases decrease in the light scattering intensity (or apparent optical absorption) is observed on the initial portions of kinetic curves of protein substrate aggregation recorded in the presence of a chaperone, namely α-crystallin (a representative of sHsp family). Such a kinetic behavior was demonstrated, for example, on studying the effect of α-crystallin on the rate of thermal aggregation of citrate synthase (EC 2.3.3.1) at 43°C [94] and β-amyloid peptide at 60°C [95]. There is a simple explanation of the unusual character of aggregation kinetic curves. Elevated temperatures cause dissociation of α-crystallin particles and decrease in the light scattering intensity. This is supported by the data obtained by us [45, 96-98].
If decrease in the light scattering intensity (or the apparent optical absorption) is observed on the initial portion of aggregation kinetic curves, a reliable determination of the initial value of the light scattering intensity I0 (or A0 value) becomes impossible, and Eqs. (1) and (2) thus cannot be used for determination of the initial rate of aggregation. In this case the differential forms of Eqs. (1) and (2) appear to be useful:
or
Analysis of the dependence of the initial rate of aggregation on the initial concentration of protein substrate [P]0 allows determination of the order of the aggregation reaction with respect to protein and a conclusion about the limiting stage of the aggregation process. The order of the aggregation reaction with respect to protein (n) is calculated by the following equation:
As will be seen below, it is important to know the value of n for quantification of the antiaggregation activity of protein chaperones.
For thermal aggregation of Phb (53°C, pH 6.8) [85] and GAPDH (45°C, pH 7.5) [84], the Kagg parameter linearly depends (n = 1) on the initial concentration of the protein. The kinetics of thermal aggregation of glutamate dehydrogenase (EC 1.4.1.2) from bovine liver at various protein concentrations was studied in [99] (50°C, pH 8.0). Based on the data, we calculated the order of aggregation with respect to protein, and it appeared to be close to a unity: n = 0.86 ± 0.1. The situation when n = 1 means that unfolding of the protein molecule proceeds with significantly lower rate than the subsequent stages of aggregation of the unfolded protein molecules.
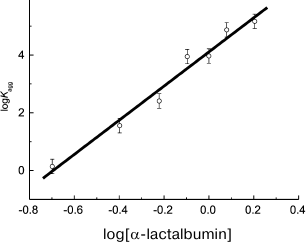
In a case when unfolding of a protein molecule is a relatively rapid process, the n parameter exceeds 1. For example, analysis of kinetic data on thermal aggregation of βL-crystallin from bovine eye lens (60°C, pH 6.8) [100] and yeast alcohol dehydrogenase (EC 1.1.1.1) (56°C, pH 7.4) [101] indicates that n is close to 2. Analogous results have been obtained for UV-irradiated GAPDH (37°C, pH 7.5, n = 2.1 ± 0.2) [84]. For aggregation of α-lactalbumin [91] and insulin [92] induced by dithiothreitol, the calculated n values significantly exceed 2, being 5.9 ± 0.4 (37°C) and 8.2 ± 0.5 (25°C), respectively. It should be noted that in order to calculate the n value, the logarithmic coordinates {log[P]0; log(Kagg)} are used. For example, calculation of n for α-lactalbumin is presented in Fig. 3.
Fig. 3. Calculation of the reaction order (n) for aggregation of a protein substrate. Based on the data presented in [91], the initial rate of α-lactalbumin aggregation is plotted versus protein concentration in logarithmic coordinates. Dimensionalities: Kagg, (photocounts/s) × min–2; α-lactalbumin concentration, mg/ml. Kagg is used as the initial rate of aggregation of α-lactalbumin. Conditions: 37°C, 20 mM dithiothreitol, 50 mM sodium phosphate buffer, pH 6.8, containing 0.15 M NaCl and 1 mM EGTA.
It is of interest that we used an equation similar to Eq. (1) for description of the initial portions of aggregation kinetic curves in experiments in which temperature increased at a constant rate [102]:
where T0 is the initial aggregation temperature, i.e. the temperature at which the light scattering intensity begins to increase, and Kagg is a parameter characterizing the aggregation rate. Parameters Kagg and T0 can be used for quantification of the ability of various agents to suppress aggregation of proteins. Applicability of Eq. (8) was demonstrated for aggregation of Phb, GAPDH, creatine kinase, and glutamate dehydrogenase.
In accord with the concept of the protein aggregation mechanism suggested by Kurganov et al. [100, 102-104], time point t = t0 (or temperature T = T0) corresponds with formation of the start aggregates. These aggregates contain hundreds of the denatured protein molecules. The start aggregates are formed via the all-or-nothing principle. Formation of intermediates with dimensions between those of non-aggregated protein and the start aggregates has not been detected.
For completeness sake, let us discuss additional methods for determination of the initial rate of aggregation. Analyzing kinetic curves of aggregation of UV-denatured Phb [105], we showed that Eq. (1) appeared to be invalid. To characterize the initial rate of aggregation, we used the time interval during which the light scattering intensity increased from the initial value I0 to the value 2I0 (t2I). To evaluate the t2I value, we used the extended exponent for description of the initial portions of kinetic curves:
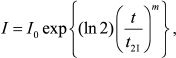 (9)
(9)where m is a constant.
Our analysis of the aggregation kinetics of UV-irradiated Phb demonstrates that a simple exponent can be used for description of the initial portions of kinetic curves:
where K and K1 are constants. This equation can be transformed into the equation containing the t2I parameter [106]:
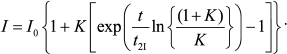 (11)
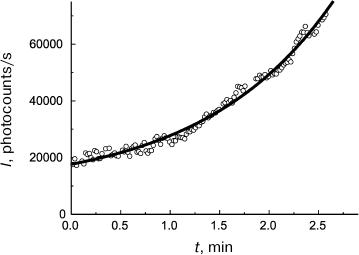
(11)As can be seen in Fig. 4, Eq. (11) quite satisfactorily describes the initial portion of the aggregation kinetic curve of UV-irradiated Phb (0.15 mg/ml) at 37°C. Parameters of Eq. (11) appear to be as follows: t2I = 1.44 ± 0.02 min and K = 0.50 ± 0.03.
Fig. 4. Use of the reciprocal value of the t2I parameter for characterization of the initial rate of aggregation. Aggregation of UV-irradiated Phb (0.15 mg/ml) time dependence of light scattering intensity (I) is plotted for the data presented in [105]. Conditions: 37°C, 80 mM Hepes, pH 6.8, containing 100 mM NaCl. Circles are experimental data. The solid line is drawn using Eq. (11) at t2I = 1.44 min and K = 0.50.
It should be noted that in contrast to the test system based on thermal aggregation of proteins, the stage of unfolding of the protein molecule is absent in the test system based on aggregation of UV-irradiated Phb. The UV-irradiated Phb molecules form the primary aggregates with hydrodynamic radius of 10.4 nm [107].
There is one more method for evaluation of the initial rate of aggregation. Our analysis of experimental data on kinetics of protein aggregation demonstrated that at time values exceeding the moment corresponding to the inflection point on kinetic curve, I or A exponentially depends on time [108-112]:
or
where Ilim and Alim are the limiting I and A values, respectively, at t → , kI is the first-order reaction rate constant, and t* is the length intercepted by the theoretical curve calculated using Eq. (12) or (13) on the horizontal line corresponding to the initial I or A values (I = I0 or A = A0). The slope of the theoretical curve at the point {t = t*, I = I0} or {t = t*, A = A0} is equal to the product kI(Ilim – I0) or kI(Alim – A0). This slope is a measure of the initial rate of aggregation.
It should be noted that the lag period on kinetic curves of aggregation can be absent, and this makes using Eqs. (1) and (2) impossible. In such situations it becomes justified to characterize the initial rate of aggregation by the kI(Ilim – I0) or kI(Alim – A0) products. This is exemplified by our analysis of the aggregation kinetics of protein of tobacco mosaic virus envelope (52°C, pH 8.0) [113].
Equations analogous to Eq. (7) can be used for determination of the order of aggregation reaction for a protein:
or
For thermal aggregation of firefly luciferase (EC 1.13.12.7) and tobacco mosaic virus coat protein [114], the n parameter appears to be 2. This means that the stage of aggregation is the rate-limiting stage of the aggregation process. It should be noted that first order with respect to protein (n = 1) was observed for thermal aggregation of creatine kinase from rabbit skeletal muscles [115] and aggregation accompanying renaturation of the pre-denatured carbonic anhydrase (EC 4.2.1.1) [116]. So, the monomolecular stage (unfolding of protein molecule in the case of creatine kinase or the initial stage of protein folding in the case of carbonic anhydrase) is the rate-limiting stage of the aggregation process.
QUANTIFICATION OF ANTIAGGREGATION ACTIVITY OF PROTEIN
CHAPERONES
Analyzing the dependence of the initial rate of aggregation (ν) on concentration of a chaperone of protein nature, the following two items should be taken into account. First, the protein–substrate binding is rather tight. The value of dissociation constants for chaperone–protein substrate complexes is several nmol/liter in order (e.g. see [117]). Usually experiments on suppression of aggregation of protein substrate are performed under conditions where the initial concentrations of the chaperone and the protein substrate significantly exceed the value of Kdiss for the chaperone–protein substrate complex. This means that dependence of the initial rate of aggregation on chaperone concentration is in fact a titration curve that gives information about the stoichiometry of the chaperone–protein substrate complex in certain cases.
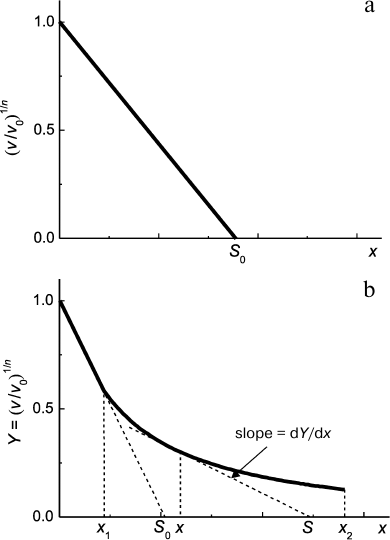
Second, in accordance with Eq. (7) protein concentration [P]0 is proportional to ν1/n. This means that decrease in protein substrate concentration (e.g. due to complex formation with substrate) should result in a proportional decrease in ν1/n value. Thus, for analysis of the antiaggregation activity of a chaperone one should use coordinates {ν1/n; [chaperone]}. The value of the relative initial rate of aggregation ν/ν0 is defined by the ratio of chaperone and protein substrate concentrations. In an ideal case, the dependence of (ν/ν0)1/n on [chaperone]/[protein substrate] ratio is a straight line (Fig. 5a). The length intercepted by the line on the x-axis (S0) characterizes the stoichiometry of the chaperone–protein substrate complex. The S0 value is calculated from the following equation:
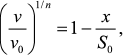 (16)
(16)where x is [chaperone]/[protein substrate] ratio.
Fig. 5. Suppression of aggregation of a protein substrate by a chaperone of protein nature. Dependence of the relative initial rate of aggregation (ν/ν0)1/n on chaperone/protein substrate concentrations ratio. The following designations are used: ν0 and ν are the initial rates of aggregation in the absence and in the presence of a chaperone, respectively; n is the power of protein concentration in Eq. (7); x = [chaperone]/[protein substrate] ratio; S is stoichiometry of chaperone–protein substrate complex. a) Formation of chaperone–protein substrate complex with constant stoichiometry S0. b) A case when the stoichiometry of chaperone/protein substrate changes on varying [chaperone]/[protein substrate] ratio in the range of x values from x1 to x2.
Calculating the complex stoichiometry in such a way, we assume that all the protein substrate is in a form able to bind to chaperone. However, if the test system based on thermal aggregation of protein is used, the initial (native) form of substrate does not bind to the chaperone, and accumulation of the unfolded form of the protein, which interacts with the chaperone, proceeds with time. Thus, there is an uncertainty in determination of protein substrate concentration. In such case we suggest calling the stoichiometry of the complex, which is defined by the length intercepted on the x-axis, as an apparent stoichiometry (S0,app). It is important that the S0,app value can be used for quantification of the antiaggregation activity of the chaperone. Dealing with one and the same test system, we can use the S0,app parameter for comparative analysis of the antiaggregation activity of various chaperones (e.g. for analysis of protective action of the wild-type small heat shock proteins and their mutant forms; intact chaperone and its chemically modified forms).
Let us consider the dependence of the initial rate of aggregation of UV-irradiated Phb on concentration of α-crystallin (37°C, pH 6.8) obtained by Roman et al. [105]. Equation (9) was used for calculation of the initial rate of aggregation ν. It is important that Phb completely denatured by UV irradiation was used as the protein substrate. The value S0 was determined from the initial portion of ν dependence on concentration of α-crystallin: S0 = 1.53 ± 0.15 moles of α-crystallin subunits per Phb subunit. It is of interest that at rather high concentration of α-crystallin, deviations from linear dependence are observed. One can suppose that the complex character of the dependence of the initial rate of aggregation on concentration of α-crystallin is caused by the dynamic structure of α-crystallin, and the initial portion of this plot corresponds with formation of protein–substrate complexes with dissociated forms of α-crystallin. Formation of α-crystallin–protein substrate complexes with the decreased adsorption capacity of α-crystallin towards the protein substrate corresponds with the second portion of ν dependence on α-crystallin concentration (with gentler slope). It should be mentioned that adsorption capacity is calculated as the reciprocal of the S value.
In a case when the dependence of the initial rate of aggregation on [chaperone]/[protein substrate] ratio appears to deviate from linearity, the following approach can be used for evaluation of the stoichiometry of the chaperone–protein substrate complex. For example, let us consider a case when the initial linear portion of the plot representing the initial rate of aggregation versus x = [chaperone]/[protein substrate] ratio transforms into a portion with gentler slope at x > x1, and the latter portion is characterized by a hyperbolic dependence at x in the range from x1 to x2 (Fig. 5b):
where Y is (ν/ν0)1/n, Y0 is Y value at x = 0, and x0.5 is x value at which Y = Y0/2. Let us choose any point within the range from x1 to x2. As can be seen in Fig. 5b, the slope of the theoretical curve at the point with coordinates (x; Y) is related to the stoichiometry of the chaperone–protein substrate complex by the following equation:
It follows that
The dY/dx derivative is calculated from Eq. (17):
Substitution of dY/dx in Eq. (19) yields an equation for evaluation of the stoichiometry of the chaperone–protein substrate complex at a particular x value within the range x1 < x < x2:
Thus, in the x range from x1 to x2 the S value increases from (x0.5 + 2x1) to (x0.5 + 2x2). As for the initial portion of (ν/ν0)1/n dependence on [chaperone]/[protein substrate] ratio (x < x1), the stoichiometry of this complex is constant and equal to S0.
The product kIAlim was used for quantification of the chaperone-like activity of natural casein and β-casein [118-120]. It is of interest that the plot representing dependence of kIAlim product on concentration of natural casein for suppression of aggregation accompanying renaturation of pre-denatured carbonic anhydrase by natural casein consists of two portions [118].
The experimental data on suppression of thermal aggregation of the catalytic subunit of protein kinase CK2 (CK2α) at 40°C by the C-terminal domain of glucose-regulated protein (grp94-CT) obtained by Itarte et al. [121] were analyzed by Kurganov [109]. The product kIAlim was used for calculation of the initial rate of aggregation. It was found that kIAlim linearly depended on the molar ratio [grp94-CT]/[CK2α]. The stoichiometry of the grp94-CT–CK2α complex was calculated from the length intercepted by the straight line on the x-axis; it appeared to be four grp94-CT molecules per CK2α molecule.
It should be noted that the plots {degree of protective action; chaperone concentration} are sometimes used as characteristics of the antiaggregation activity of protein chaperones (α-crystallin and others). The degree of protective action (P) is calculated from the kinetic curve of aggregation:
where A0 and A are the apparent optical absorption values in the absence and in the presence of chaperone, respectively, at t = 1 h. The light scattering intensity values can obviously be used instead of the apparent optical absorption values. For example, this method was used in [122-125]. However, such quantifications of the antiaggregation activity of protein chaperones should be used with caution, since A0 and A values are usually related with different portions of kinetic curves of aggregation. The A0 value can be related to the area of limiting values of the apparent optical absorption, whereas the A value can be related to the initial portion of the kinetic curve.
QUANTIFICATION OF ANTIAGGREGATION ACTIVITY OF CHEMICAL
CHAPERONES
The protective action of chemical chaperones manifests itself in decrease in the initial rate of protein substrate aggregation (ν) in the presence of chemical chaperones. In the simplest case, ν hyperbolically depends on chaperone concentration (L):
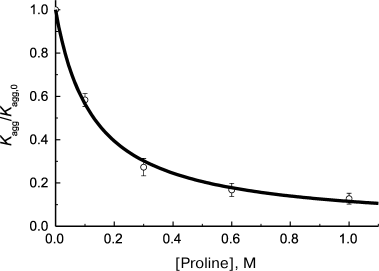
where ν0 is the initial rate of aggregation in the absence of chaperone and Kd is the dissociation constant. This equation was used for example by Wilcken et al. [126] for analysis of suppression of aggregation of mutant protein p53 by medical preparations (37°C, pH 7.2). The initial rate of aggregation was calculated using Eq. (1). Analogous hyperbolic dependence of the initial rate of protein substrate aggregation on concentration of chemical chaperone was observed on suppression of thermal aggregation of Phb by proline at 48°C [87] (Fig. 6). The calculated Kd value appeared to be 0.13 ± 0.01 M.
Fig. 6. Suppression of aggregation of protein substrate by chemical chaperone. Dependence of the relative initial rate of aggregation (Kagg/Kagg,0) of Phb (0.3 mg/ml) on proline concentration (48°C, 0.08 M Hepes, pH 6.8, containing 0.1 M NaCl) is plotted for the data presented in [87]. Circles are experimental data. The solid curve is drawn using Eq. (23) for Kd = 0.13 M.
Studying suppression of aggregation of UV-irradiated GAPDH by chemical chaperone HP-β-CD [84], we showed that the dependence of the initial rate of aggregation (ν) expressed by the Kagg parameter on concentration of chemical chaperone is described by the Hill equation widely used in enzymology [127]:
where [L]0.5 is the half-saturation concentration, that is chaperone concentration at which ν/ν0 = 0.5, and h is the Hill coefficient. For suppression of aggregation of UV-irradiated GAPDH by HP-β-CD, the following values of these parameters were obtained: [L]0.5 = 11 ± 1 mM and h = 1.8 ± 0.2 (37°C). The Hill coefficient values exceeding unity indicate that there are positive cooperative interactions between the chaperone-binding sites in the protein substrate molecule [127]. The [L]0.5 parameter can be considered as a characteristic of chaperone affinity to protein substrate. The lower the [L]0.5 value, the higher is this affinity. It is important to note that the form of the plot representing dependence of initial rate on concentration of chemical chaperone should remain unchanged on varying protein substrate concentration. This was observed, for example, for curves of dependence of the initial rate of aggregation of UV-irradiated Phb on proline concentration [105]. For suppression of aggregation of UV-irradiated Phb by proline, the following values of parameters of Eq. (24) were obtained: [L]0.5 = 0.19 ± 0.01 M and h = 1.6 ± 0.1 (37°C). It should be noted that in both cases UV-irradiated protein – GAPDH [84] or Phb [105] – was used as the protein substrate. Test systems of this type allow recording the effect of chemical chaperone immediately at the stage of aggregation of protein substrate. In the commonly used test systems, e.g. in those based on thermal aggregation of proteins, the total effect of chemical chaperone includes the action of chaperone on the aggregation stage and its action on the preceding stages (see e.g. [87-90]).
RELATIONSHIP BETWEEN INITIAL RATE OF AGGREGATION AND LAG
PERIOD
Analyzing the relationship between lag period (t0) and the rate of growth of amyloid-like structures (kg), Fändrich [128] concluded that kg is proportional to the reciprocal of the t0 value:
where α is a constant. In his opinion, the observed tendency means that there is a kinetic correlation between the efficiency of nucleus seed formation and the rate of aggregate growth. There is particular interest to clarify whether Eq. (25) is a universal one and is fulfilled in the case of aggregation resulting in formation of amorphous aggregates.
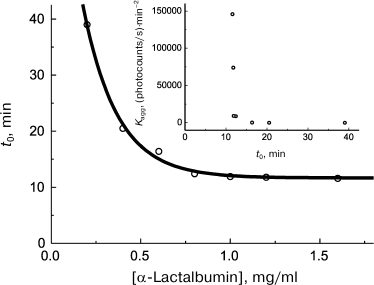
First of all, let us note that the availability of quantitative methods that allow reliable determination of such characteristics as the lag period and initial rate of aggregation on kinetic curves provides more rigorous treatment of the problem of existence of a certain relationship between lag period and the initial rate of aggregation. Analysis of the data on kinetics of heat- and dithiothreitol-induced aggregation of proteins available in the literature demonstrates that there usually exists a lower limit to t0 values. For example, let us discuss kinetics of the dithiothreitol-induced aggregation of α-lactalbumin. With increase in α-lactalbumin concentration, the lag period decreases and attains the limiting value of 11.6 min at sufficiently high protein concentrations (Fig. 7). The relationship between the initial rate of aggregation defined by the value of the Kagg parameter and the lag period (t0 parameter) is presented in Fig. 7 (inset). Kagg increases with increase in protein concentration in accord with Eq. (7) for n = 5.9. As can be seen in the inset (Fig. 7), the inverse proportionality of the aggregation rate to lag period suggested by Fändrich [128] is not obeyed, and all the Kagg values are located at t0 > 11.6 min. Existence of the lower limit to lag period seems to be caused by kinetic features of the nucleation stage.
Fig. 7. Analysis of relationship between the initial rate of aggregation and lag period. Kinetic characteristics of α-lactalbumin aggregation induced by dithiothreitol (37°C, 20 mM dithiothreitol, 50 mM sodium phosphate buffer, pH 6.8, containing 0.15 M NaCl and 1 mM EGTA). Dependence of lag period (t0) on α-lactalbumin concentration is plotted for the data presented in [91]. Inset: relationship between Kagg and t0 parameters.
The lower limit to t0 values can manifest itself while studying the effect of chemical chaperones on the rate of aggregation of protein substrates. We observed acceleration of GAPDH aggregation (45°C, 10 mM sodium phosphate buffer, pH 7.5, containing 0.1 M NaCl) in the presence of HP-β-CD [90]; the data suggest that HP-β-CD possesses “anti-chaperone” activity. Destabilizing action of HP-β-CD results in the increased rate of GAPDH aggregation; this is supported by data of differential scanning calorimetry. It has been found that with increase in HP-β-CD concentration the lag period decreases from t0 = 3.0 min (the value measured in the absence of HP-β-CD) to t0 = 1.6 min at sufficiently high HP-β-CD concentrations.
COOPERATIVE ACTION OF CHAPERONES
Protective action of chaperones of protein nature can be modulated in the presence of low molecular weight chemical chaperones. As shown in [129-131], the chaperone-like activity of α-crystallin increases in the presence of arginine. Such effect of arginine is supposed to be related with increased mobility of the quaternary structure of α-crystallin particles [130].
Since in general case each chaperone (protein chaperone or chemical one) influences the rate of aggregation of a protein substrate, the rigorous quantitative methods should be used to characterize the cooperative action of chaperones. For this, the j parameter suggested by us for analysis of the cooperative action of inhibitors can be used [132]:
In this equation, j is the extent of inhibition: i1 = 1 – ν1/ν0 for inhibitor 1, i2 = 1 – ν2/ν0 for inhibitor 2, and i1,2 = 1 – ν1,2/ν0 for a mixture of inhibitors 1 and 2 (ν0 is the initial rate of aggregation in the absence of inhibitors, ν1, ν2, and ν1,2 are the initial rates of aggregation in the presence of inhibitor 1, inhibitor 2, or a mixture of inhibitors 1 and 2, respectively). In a case when the action of one inhibitor is independent of the presence of another one, the j parameter is equal to unity. A case when j > 1 corresponds to synergism, and that when j < 1 corresponds to antagonism in the cooperative action of two inhibitors.
We used the j parameter for analysis of the cooperative action of α-crystallin and proline on the rate of aggregation of UV-irradiated Phb [105]. To characterize the initial rate of aggregation, the 1/t2I parameter was used. In a case when proline concentration was 0.15 M, we observed a slight antagonism in the cooperative action of α-crystallin and proline (the calculated j values were in the range 0.81-0.91). However, at higher proline concentration (0.5 M) the effect of each inhibitor (α-crystallin and proline) was independent from the other one.
The j parameter can be also used for analysis of the cooperative action of protein chaperones. For example, the cooperative action of α-crystallin and β-casein on the dithiothreitol-induced aggregation of insulin from bovine pancreas was studied in [133]. To characterize the initial rate of aggregation, the kIAlim parameter was used. Our analysis of the data presented in [133] demonstrates that j is close to unity. Thus, the two chaperones act independently from one another.
It should be noted that to characterize the antiaggregation activity of α-crystallin in the presence of arginine, the degree of protective action P defined by Eq. (22) was used [129, 131]. The P value is obviously equal to the extent of inhibition i in Eq. (26). Thus, to calculate the j parameter characterizing the cooperative protective action of a chaperone of protein nature and a chemical chaperone, an equation identical to Eq. (26) can be used:
In this equation, P is the degree of protective action: P1 – for chaperone 1, P2 – for chaperone 2, and P1,2 – for a mixture of chaperones 1 and 2.
CONCLUSION
Analysis of the data on the action of chaperones of protein nature and of chemical chaperones published in the last 20 years demonstrates that the lack of thorough treatment of kinetic data results in the loss of important information that can be useful for understanding the mechanism of protective action of chaperones. It is obvious that in the cases of chaperones of protein nature, the dependence of the initial rate of protein substrate aggregation on chaperone concentration contains information about the stoichiometry of the chaperone–protein substrate complex. However, special investigations on estimation of the real concentration of protein substrate should be performed for each of the test systems used. For example, detailed information about the rate of protein denaturation is required for the aggregation test systems in which the stage of aggregation is preceded by the stage of unfolding of the protein molecule (test systems based on thermal aggregation of proteins or those based on the dithiothreitol-induced aggregation of proteins). It should be noted that kinetic evaluation of the stoichiometry of the chaperone–protein substrate complex that is based on analysis of dependence of the initial rate of aggregation on chaperone concentration is to be supported by direct experiments on determination of stoichiometry, e.g. experiments including separation of components of the system using size-exclusion chromatography and subsequent quantitative electrophoresis of the components in polyacrylamide gel in the presence of SDS.
Now a large number of test systems of various types are used for quantification of the antiaggregation activity of chaperones. Studies on comparison of test systems and selection of systems allowing more reliable calculation of the antiaggregation activity and evaluation of the stoichiometry of a chaperone–protein substrate complex become possible.
Use of equations for calculation of the initial rate of protein aggregation and equations describing the dependence of the initial rate of aggregation of a protein substrate on the concentration of a chemical chaperone described in this review allows rigorous quantification of the antiaggregation activity of chemical chaperones and also provides the possibility for selection of agents efficiently suppressing aggregation of proteins and is of interest for solution of biotechnological problems.
The equations suggested for the cooperative action of inhibitors of enzymatic reactions appear to be useful for quantification of the cooperative action of chaperones, in particular, chaperones of protein nature and chemical chaperones. So, the effects of synergism and antagonism in cooperative action of chaperones can be quantitatively characterized.
This work was financially supported by the Russian Foundation for Basic Research (grant No. 11-04-00932-a) and the Program of Presidium of the Russian Academy of Sciences “Molecular and Cell Biology”.
REFERENCES
1.Hartl, F. U., and Hayer-Hartl, M. (2002)
Science, 295, 1852-1858.
2.Markossian, K. A., and Kurganov, B. I. (2004)
Biochemistry (Moscow), 69, 971-984.
3.Ellis, R. J. (2011) in Folding for the
Synapse (Wyttenbach, A., and O’Connor, V., eds.) Springer,
New York, pp. 9-34.
4.Invernizzi, G., Papaleo, E., Sabate, R., and
Ventura, S. (2012) Int. J. Biochem. Cell Biol., 44,
1541-1554.
5.Kurganov, B. I. (2012) Biochem. Anal.
Biochem., 1, e107.
6.Tyedmers, J., Mogk, A., and Bukau, B. (2010)
Nat. Rev. Mol. Cell. Biol., 11, 777-788.
7.Richter, K., Haslbeck, M., and Buchner, J. (2010)
Mol. Cell, 40, 253-266.
8.Hartl, F. U., Bracher, A., and Hayer-Hartl, M.
(2010) Nature, 475, 324-332.
9.Van Montfort, R., Slingsby, C., and Vierling, E.
(2002) Adv. Protein Chem., 59, 105-156.
10.Narberhaus, F. (2002) Microbiol. Mol. Biol.
Rev., 66, 64-93.
11.Haslbeck, M., and Buchner, J. (2002) Prog.
Mol. Subcell. Biol., 28, 37-59.
12.Panasenko, O. O., Kim, M. V., and Gusev, N. B.
(2003) Uspekhi Biol. Khim., 43, 59-98.
13.Haslbeck, M., Franzmann, T., Weinfurtner, D., and
Buchner, J. (2005) Nat. Struct. Mol. Biol., 12,
842-846.
14.Sun, Y., and MacRae, T. H. (2005) Cell. Mol.
Life Sci., 62, 2460-2476.
15.Nakamoto, H., and Vígh, L. (2007) Cell.
Mol. Life Sci., 64, 294-306.
16.Vos, M. J., Hageman, J., Carra, S., and Kampinga,
H. H. (2008) Biochemistry, 47, 7001-7011.
17.Kappe, G., Boelens, W. C., and de Jong, W. W.
(2010) Cell Stress Chaperones, 15, 457-461.
18.Baldwin, A. J., Lioe, H., Hilton, G. R., Baker,
L. A., Rubinstein, J. L., Kay, L. E., and Benesch, J. L. P. (2011)
Structure, 19, 1855-1863.
19.Baldwin, A. J., Lioe, H., Robinson, C. V., Kay,
L. E., and Benesch, J. L. P. (2011) J. Mol. Biol., 413,
297-309.
20.Jehle, S., Vollmar, B. S., Bardiaux, B., Dove, K.
K., Rajagopal, P., Gonen, T., Oschkinat, H., and Klevit, R. E. (2011)
Proc. Natl. Acad. Sci. USA, 108, 6409-6414.
21.Mymrikov, E. V., Seit-Nebi, A. S., and Gusev, N.
B. (2011) Physiol. Rev., 91, 1123-1159.
22.Hilton, G. R., Lioe, H., Stengel, F., Baldwin, A.
J., and Benesch, J. L. P. (2013) Top. Curr. Chem., 328,
69-98.
23.Lee, G. J., Roseman, A. M., Saibil, H. R., and
Vierling, E. (1997) EMBO J., 16, 659-671.
24.Ehrnsperger, M., Graber, S., Gaestel, M., and
Buchner, J. (1997) EMBO J., 16, 221-229.
25.Veinger, L., Diamant, S., Buchner, J., and
Goloubinoff, P. (1998) J. Biol. Chem., 273,
11032-11037.
26.Lee, G. J., and Vierling, E. (2000) Plant
Physiol., 122, 189-198.
27.Wang, K., and Spector, A. (2000) Eur. J.
Biochem., 267, 4705-4712.
28.Bova, M. P., Ding, L. L., Horwitz, J., and Fung,
B. K. (1997) J. Biol. Chem., 272, 29511-29517.
29.Sun, T. X., Akhtar, N. J., and Liang, J. J.
(1998) FEBS Lett., 430, 401-404.
30.Bova, M. P., McHaourab, H. S., Han, Y., and Fung,
B. K. (2000) J. Biol. Chem., 275, 1035-1042.
31.Bova, M. P., Huang, Q., Ding, L., and Horwitz, J.
(2002) J. Biol. Chem., 277, 38468-38475.
32.Baldwin, A. J., Hilton, G. R., Lioe, H.,
Bagneris, C., Benesch, J. L., and Kay, L. E. (2011) J. Mol.
Biol., 413, 310-320.
33.Baldwin, A. J., Walsh, P., Hansen, D. F., Hilton,
G. R., Benesch, J. L. P., Sharpe, S., and Kay, L. E. (2012) J. Am.
Chem. Soc., 134, 15343-15350.
34.Basha, E., O’Neill, H., and Vierling, E.
(2012) Trends Biochem. Sci., 37, 106-117.
35.Stromer, T., Ehrnsperger, M., Gaestel, M., and
Buchner, J. (2003) J. Biol. Chem., 278, 18015-18021.
36.Friedrich, K. L., Giese, K. C., Buan, N. R., and
Vierling, E. (2004) J. Biol. Chem., 279, 1080-1089.
37.Benesch, J. L., and Ruotolo, B. T. (2011)
Curr. Opin. Struct. Biol., 21, 641-649.
38.Stengel, F., Baldwin, A. J., Painter, A. J.,
Jaya, N., Basha, E., Kay, L. E., Vierling, E., Robinson, C. V., and
Benesch, J. L. P. (2010) Proc. Natl. Acad. Sci. USA, 107,
2007-2012.
39.Buchner, J., Schmidt, M., Fuchs, M., Jaenicke,
R., Rudolph, R., Schmid, F. X., and Kiefhaber, T. (1991)
Biochemistry, 30, 1586-1591.
40.Hartman, D. J., Surin, B. P., Dixon, N. E.,
Hoogenraad, N. J., and Hoj, P. B. (1993) Proc. Natl. Acad. Sci.
USA, 90, 2276-2280.
41.Weber, F., Keppel, F., Georgopoulos, C.,
Hayer-Hartl, M. K., and Hartl, F. U. (1998) Nat. Struct. Biol.,
5, 977-985.
42.Naletova, I. N., Muronetz, V. I., and
Schmalhausen, E. V. (2006) Biochim. Biophys. Acta, 1764,
831-838.
43.Huq, S., Sueoka, K., Narumi, S., Arisaka, F., and
Nakamoto, H. (2010) Biosci. Biotechnol. Biochem., 74,
2273-2280.
44.Li, Y., Zheng, Z., Ramsey, A., and Chen, L.
(2010) J. Pept. Sci., 16, 693-700.
45.Markossian, K. A., Golub, N. V., Chebotareva, N.
A., Asryants, R. A., Naletova, I. N., Muronez, V. I., Muranov, K. O.,
and Kurganov, B. I. (2010) Protein J., 29, 11-25.
46.Eronina, T. B., Chebotareva, N. A., Bazhina, S.
G., Kleymenov, S. Y., Naletova, I. N., Muronetz, V. I., and Kurganov,
B. I. (2010) Macromol. Biosci., 10, 768-774.
47.Braig, K., Otwinowski, Z., Hegde, R., Boisvert,
D. C., Joachimiak, A., Horwich, A. L., and Sigler, P. B. (1994)
Nature, 371, 578-586.
48.Hartl, F. U., and Hayer-Hartl, M. (2009)
Nat. Struct. Mol. Biol., 16, 574-581.
49.Clare, D. K., Bakkes, P. J., van Heerikhuizen,
V., van der Vies, S. M., and Saibil, H. R. (2009) Nature,
457, 107-110.
50.Jewett, A. I., and Shea, J.-E. (2010) Cell.
Mol. Life Sci., 67, 255-276.
51.Marchenkov, V. V., and Semisotnov, G. V. (2009)
Int. J. Mol. Sci., 10, 2066-2083.
52.Wiech, H., Buchner, J., Zimmermann, R., and
Jakob, U. (1992) Nature, 358, 169-170.
53.Jakob, U., Lilie, H., Meyer, I., and Buchner, J.
(1995) J. Biol. Chem., 270, 7288-7294.
54.Youker, R. T., Walsh, P., Beilharz, T., Lithgow,
T., and Brodsky, J. L. (2004) Mol. Biol. Cell, 15,
4787-4797.
55.Muller, L., Schaupp, A., Walerych, D., Wegele,
H., and Buchner, J. (2004) J. Biol. Chem., 279,
48846-48854.
56.Evans, C. G., Wisen, S., and Gestwicki, J. E.
(2006) J. Biol. Chem., 281, 33182-33191.
57.Wayne, N., and Bolon, D. N. (2010) J. Mol.
Biol., 401, 931-939.
58.Taneja, S., and Ahmad, F. (1994) Biochem.
J., 303, 147-153.
59.Xie, G., and Timasheff, S. N. (1997) Biophys.
Chem., 64, 25-43.
60.Anjum, F., Rishi, V., and Ahmad, F. (2000)
Biochim. Biophys. Acta, 1476, 75-84.
61.Bolen, D. W. (2001) Methods Mol. Biol.,
168, 17-36.
62.Rosgen, J., Pettitt, B. M., and Bolen, D. W.
(2005) Biophys. J., 89, 2988-2997.
63.Kumar, R. (2009) Arch. Biochem. Biophys.,
491, 1-6.
64.Politi, R., and Harries, D. (2010) Chem.
Commun., 46, 6449-6451.
65.Welch, W. J., and Brown, C. R. (1996) Cell
Stress Chaperones, 1, 109-115.
66.Papp, E., and Csermely, P. (2006) Handb. Exp.
Pharmacol., 172, 417-436.
67.Paul, S., Punam, S., and Chaudhuri, T. K. (2007)
FEBS J., 274, 6000-6010.
68.Leandro, P., and Gomes, C. M. (2008) Mini Rev.
Med. Chem., 8, 901-911.
69.Rajan, R. S., Tsumoto, K., Tokunaga, M.,
Tokunaga, H., Kita, Y., and Arakawa, T. (2011) Curr. Med. Chem.,
18, 1-15.
70.Singer, M. A., and Lindquist, S. (1998) Mol.
Cell, 1, 639-648.
71.Arora, A., Ha, C., and Park, C. B. (2004) FEBS
Lett., 564, 121-125.
72.Ignatova, Z., and Gierasch, L. M. (2007)
Methods Enzymol., 428, 355-372.
73.Xia, Y., Park, Y. D., Mu, H., Zhou, H. M., Wang,
X. Y., and Meng, F. G. (2007) Int. J. Biol. Macromol.,
40, 437-443.
74.Hamada, H., Arakawa, T., and Shiraki, K. (2009)
Curr. Pharm. Biotechnol., 10, 400-407.
75.Nayak, A., Lee, C. C., McRae, G. J., and Belfort,
G. (2009) Biotechnol. Prog., 25, 1508-1514.
76.Macchi, F., Eisenkolb, M., Kiefer, H., and Otzen,
D. E. (2012) Int. J. Mol. Sci., 13, 3801-3819.
77.Charman, S. A., Mason, K. L., and Charman, W. N.
(1993) Pharm. Res., 10, 954-962.
78.Yu, J., Bakhos, L., Chang, L., Holterman, M. J.,
Klein, W. L., and Venton, D. L. (2002) J. Mol. Neurosci.,
19, 51-55.
79.Tavornvipas, S., Tajiri, S., Hirayama, F., Arima,
H., and Uekama, K. (2004) Pharm. Res., 21, 2369-2376.
80.Tavornvipas, S., Hirayama, F., Takeda, S., Arima,
H., and Uekama, K. (2006) J. Pharm. Sci., 95,
2722-2729.
81.Bajorunaite, E., Cirkovas, A., Radzevicius, K.,
Larsen, K. L., Sereikaite, J., and Bumelis, V. A. (2009) Int. J.
Biol. Macromol., 44, 428-434.
82.Samra, H. S., He, F., Bhambhani, A., Pipkin, J.
D., Zimmerer, R., Joshi, S. B., and Middaugh, C. R. (2010) J. Pharm.
Sci., 99, 2800-2818.
83.Maloletkina, O. I., Markossian, K. A., Belousova,
L. V., Kleimenov, S. Y., Orlov, V. N., Makeeva, V. F., and Kurganov, B.
I. (2010) Biophys. Chem., 148, 121-130.
84.Maloletkina, O. I., Markossian, K. A.,
Chebotareva, N. A., Asryants, R. A., Kleymenov, S. Y., Poliansky, N.
B., Muranov, K. O., Makeeva, V. F., and Kurganov, B. I. (2012)
Biophys. Chem., 163-164, 11-20.
85.Kurganov, B. I. (1998) Biochemistry
(Moscow), 63, 364-366.
86.Ferrone, F. (1999) Methods Enzymol.,
309, 256-274.
87.Eronina, T. B., Chebotareva, N. A., Bazhina, S.
G., Makeeva, V. F., Kleymenov, S. Y., and Kurganov, B. I. (2009)
Biophys. Chem., 141, 66-74.
88.Eronina, T. B., Chebotareva, N. A., Kleymenov, S.
Y., Roman, S. G., Makeeva, V. F., and Kurganov, B. I. (2010)
Biopolymers, 93, 986-993.
89.Maloletkina, O. I., Markosyan, K. A., Asryants,
R. A., Orlov, V. N., and Kurganov, B. I. (2009) Dokl. Biochem.
Biophys., 427, 199-201.
90.Maloletkina, O. I., Markossian, K. A., Asryants,
R. A., Semenyuk, P. I., Makeeva, V. F., and Kurganov, B. I. (2010)
Int. J. Biol. Macromol., 46, 487-492.
91.Bumagina, Z. M., Gurvits, B. Y., Artemova, N. V.,
Muranov, K. O., and Kurganov, B. I. (2010) Biophys. Chem.,
146, 108-117.
92.Bumagina, Z., Gurvits, B., Artemova, N., Muranov,
K., and Kurganov, B. (2010) Int. J. Mol. Sci., 11,
4556-4579.
93.Markov, D. I., Pivovarova, A. V., Chernik, I. S.,
Gusev, N. B., and Levitsky, D. I. (2008) FEBS Lett., 582,
1407-1412.
94.Bhattacharyya, J., Shipova, E. V., Santhoshkumar,
P., Sharma, K. K., and Ortwerth, B. J. (2007) Biochemistry,
46, 14682-14692.
95.Sgarbossa, A., Buselli, D., and Lenci, F. (2008)
FEBS Lett., 582, 3288-3292.
96.Khanova, H. A., Markossian, K. A., Kleimenov, S.
Y., Levitsky, D. I., Chebotareva, N. A., Golub, N. V., Asryants, R. A.,
Muronetz, V. I., Saso, L., Yudin, I. K., Muranov, K. O., Ostrovsky, M.
A., and Kurganov, B. I. (2007) Biophys. Chem., 125,
521-531.
97.Meremyanin, A. V., Eronina, T. B., Chebotareva,
N. A., and Kurganov, B. I. (2008) Biopolymers, 89,
124-134.
98.Chebotareva, N. A., Kurganov, B. I., Asryants, R.
A., Muranov, K. O., and Ostrovsky, M. A. (2009) Dokl. Biochem.
Biophys., 428, 245-248.
99.Sabbaghian, M., Ebrahim-Habibi, A., and
Nemat-Gorgani, M. (2009) Int. J. Biol. Macromol., 44,
156-162.
100.Khanova, H. A., Markossian, K. A., Kurganov, B.
I., Samoilov, A. M., Kleimenov, S. Y., Levitsky, D. I., Yudin, I. K.,
Timofeeva, A. C., Muranov, K. O., and Ostrovsky, M. A. (2005)
Biochemistry, 44, 15480-15487.
101.Markossian, K. A., Golub, N. V., Khanova, H.
A., Levitsky, D. I., Poliansky, N. B., and Kurganov, B. I. (2008)
Biochim. Biophys. Acta, 1784, 1286-1293.
102.Eronina, T., Borzova, V., Maloletkina, O.,
Kleymenov, S., Asryants, R. A., Markossian, K. A., and Kurganov, B.
(2011) PLoS One, 6, e22154.
103.Golub, N., Meremyanin, A., Markossian, K.,
Eronina, T., Chebotareva, N. A., Asryants, R., Muronets, V., and
Kurganov, B. (2007) FEBS Lett., 581, 4223-4227.
104.Markossian, K. A., Kurganov, B. I., Levitsky,
D. I., Khanova, H. A., Chebotareva, N. A, Samoilov, A. M., Eronina, T.
B., Fedurkina, N. V., Mitskevich, L. G., Meremyanin, A. V., Kleymenov,
S. Yu., Makeeva, V. F., Muronets, V. I., Naletova, I. N., Shalova, I.
N., Asryants, R. A., Schmalhausen, E. V., Saso, L., Panyukov, Yu. V.,
Dobrov, E. N., Yudin, I. K., Timofeeva A. C., Muranov, K. O., and
Ostrovsky, M. A. (2006) in Protein Folding: New Research
(Obalinsky, T. R., ed.) Nova Science Publishers Inc., New York, pp.
89-171.
105.Roman, S. G., Chebotareva, N. A., and Kurganov,
B. I. (2012) Int. J. Biol. Macromol., 50, 1341-1345.
106.Kurganov, B. (2013) Biochem. Anal.
Biochem., 2, e107.
107.Roman, S. G., Chebotareva, N. A., Eronina, T.
B., Kleymenov, S. Yu., Makeeva, V. F., Muranov, K. O., Poliansky, N.
B., and Kurganov, B. I. (2011) Biochemistry, 50,
10607-10623.
108.Kurganov, B. I. (2002) Uspekhi Biol.
Khim., 42, 89-138.
109.Kurganov, B. I. (2002) Biochemistry
(Moscow), 67, 409-422.
110.Kurganov, B. I. (2002) Tsinghua Science and
Technology, 7, 331-339.
111.Kurganov, B. I. (2005) in Chemical and
Biological Kinetics. New Horizons, Vol. 2 (Biological
Kinetics) (Burlakova, E. B., and Varfolomeev, S. D., eds.)
Koninklijke Brill NV, Leiden, The Netherlands, pp. 251-279.
112.Wang, K., and Kurganov, B. I. (2003)
Biophys. Chem., 106, 97-109.
113.Kurganov, B. I., Rafikova, E. R., and Dobrov,
E. N. (2002) Biochemistry (Moscow), 67, 525-533.
114.Kurganov, B. I., Dobrov, E. N., and Rafikova,
E. R. (2002) in Proc. II Int. Symp. “Problems of
Biochemistry, Radiation and Astrobiology”, May 29-June
1 2001, Dubna, The United Nuclear Research Institute Publishers, pp.
100-104.
115.Fedurkina, N. V., Belousova, L. V., Mitskevich,
L. G., Zhou, H. M., Chang, Z., and Kurganov, B. I. (2006)
Biochemistry (Moscow), 71, 325-331.
116.Khodarahmi, R., Beyrami, M., and Soori, H.
(2008) Arch. Biochem. Biophys., 477, 67-76.
117.Mayr, C., Richter, K., Lilie, H., and Buchner,
J. (2000) J. Biol. Chem., 275, 34140-34146.
118.Khodarahmi, R., Beyrami, M., and Soori, H.
(2008) Arch. Biochem. Biophys., 477, 67-76.
119.Yousefi, R., Shchutskaya, Y. Y., Zimny, J.,
Gaudin, J. C., Moosavi-Movahedi, A. A., Muronetz, V. I., Zuev, Yu. F.,
Chobert, J.-M., and Haertle, T. (2009) Biopolymers, 91,
623-632.
120.Zakharchenko, N. L., Konnova, T. A., Gogoleva,
N. E., Fajzullin, D. A., Ertle, T., and Zuev, Yu. F. (2012) Bioorg.
Khim., 38, 223-228.
121.Roher, N., Miro, F., Boldyreff, B., Llorens,
F., Plana, M., Issinger, O. G., and Itarte, E. (2001) Eur. J.
Biochem., 268, 429-436.
122.Raman, B., Ramakrishna, T., and Rao, C. M.
(1995) FEBS Lett., 365, 133-136.
123.Srinivas, V., Datta, S. A., Ramakrishna, T.,
and Rao, Ch. M. (2001) Mol. Vision, 7, 114-119.
124.Ganadu, M. L., Aru, M., Mura, G. M., Coi, A.,
Mlynarz, P., and Kozlowski, H. (2004) J. Inorg. Biochem.,
98, 1103-1109.
125.Spinozzi, F., Mariani, P., Rustichelli, F.,
Amenitsch, H., Bennardini, F., Mura, G. M., Coi, A., and Ganadu, M. L.
(2006) Biochim. Biophys. Acta, 1764, 677-687.
126.Wilcken, R., Wang, G., Boeckler, F. M., and
Fersht, A. R. (2012) Proc. Natl. Acad. Sci. USA, 109,
13584-13589.
127.Kurganov, B. I. (1982) Allosteric Enzymes.
Kinetic Behaviour, John Wiley & Sons, Chichester, pp.
56-60.
128.Fandrich, M. (2007) J. Mol. Biol.,
365, 1266-1270.
129Srinivas, V., Raman, B., Rao, K. S., Ramakrishna, T., and Rao, Ch. M.
(2003) Protein Sci., 12, 1262-1270.
130.Srinivas, V., Raman, B., Rao, K. S.,
Ramakrishna, T., and Rao, Ch. M. (2005) Mol. Vis., 11,
249-255.
131.Ecroyd, H., and Carver, J. A. (2008) FEBS
J., 275, 935-947.
132.Silonova, G. V., Livanova, N. B., and Kurganov,
B. I. (1969) Mol. Biol. (Moscow), 3, 768-778.
133.Yousefi, R., and Jalili, S. (2011) Colloids
Surf. B. Biointerfaces, 88, 497-504.