Quantum Chemical Studies of the Catalytic Mechanism of N-Terminal Nucleophile Hydrolase

---

G. G. Chilov¹, A. V. Sidorova², and V. K. Svedas^1,2**

¹Belozersky Institute of Physicochemical Biology, Lomonosov Moscow State University, 119992 Moscow, Russia

² Faculty of Bioengineering and Bioinformatics, Lomonosov Moscow State University, 119992 Moscow, Russia; fax: (495) 939-2355;; E-mail: vytas@belozersky.msu.ru

^* To whom correspondence should be addressed.

Received December 29, 2006; Revision received February 9, 2007

---

Modeling of the catalytic mechanism of penicillin acylase, a member of the N-terminal nucleophile hydrolase superfamily, is for the first time conducted at ab initio quantum chemistry level. The uniqueness of this family of enzymes is that their active site lacks His and Asp (Glu) residues, comprising together with a serine residue the classical catalytic triad. The current investigation confirms that the amino group of the N-terminal serine residue in N-terminal hydrolases is capable of activating its own hydroxyl group. Using the MP2/RHF method with the 6--31+G** basis set, stationary points on the potential energy surface of the considered molecular system were located, corresponding to local minima (complexes of reagents, products, intermediate) and to saddle points (transition states). It turned out that the stage of acyl-serine formation proceeds via two transition states; the first one, which separates reagents from the so-called tetrahedral intermediate, has the highest relative energy (30 kcal/mol). In contrast to recently proposed empiric suggestions, we have found that participation of a bridging water molecule in proton shuttling is not necessary for the catalysis. The quantum chemical calculations showed a crucial role of a specific solvation in decreasing the activation barrier of the reaction by approximately 10 kcal/mol.

---

KEY WORDS: penicillin acylase, Ntn-hydrolase, catalytic mechanism, quantum chemistry

DOI: 10.1134/S0006297907050057

Abbreviations: MP2) Mõller-Plesset second order method; Ntn-hydrolase) N-terminal nucleophile hydrolase; PA) penicillin acylase; PES) potential energy surface; RHF) restricted Hartree-Fock method.

Penicillin acylase (PA) from Escherichia coli (EC 3.5.1.11, hydrolase class, amidohydrolase family, hydrolyzing linear amides) catalyzes hydrolysis of natural penicillins to yield 6-aminopenicillanic acid--a key intermediate for preparation of semi-synthetic antibiotics. The acyl-enzyme mechanism of PA action, according to which N-terminal serine hydroxyl group was acylated, was suggested before the X-ray structure of the enzyme was solved. This hypothesis was supported by experiments on the enzyme inactivation with phenylmethylsulfonyl fluoride, which specifically acylated a serine residue [1, 2], and further reactivation of the enzyme in the presence of an external nucleophile. Recent studies of the enzyme crystal structure and its complexes with inhibitors [3-6] confirmed these suggestions.

In 1995, N-terminal nucleophile (Ntn) enzymes were recognized as a novel distinct structural class [3, 7]. The typical fold of the Ntn-enzyme family consists of a four layered alphabetabetaalpha-core structure, formed by alpha-helices and two antiparallel beta-sheets. Mature Ntn-enzymes are formed by autocatalytic posttranslational modification. The Ntn-family can be further divided into Ntn-hydrolases (penicillin-G-acylase and penicillin-V-acylase) and Ntn-transferases (isopenicillin-N-acyltransferase) [7-9].

X-Ray structures of PA with its competitive inhibitor, phenylacetic acid, and with irreversible inhibitor, phenylmethylsulfonyl fluoride, supported the catalytic mechanism with a formation of acyl-enzyme intermediate, and showed that the key catalytic serine residue was N-terminal Serbeta1. However, there were no residues such as His, Asp, or Glu in the proximity of Serbeta1, which usually are present in the active site of serine hydrolases and take part in the enzymatic reactions proceeding via the general acid/base catalytic mechanism. Thus, the novel feature of the enzyme catalytic mechanism was that the nucleophile, which attacks the carbonyl carbon of the scissile amide bond, and the base, which facilitates the attack by accepting the proton from the nucleophile, were located at the same N-terminal amino acid. The enzyme family, correspondingly, obtained the acronym of Ntn-enzymes.

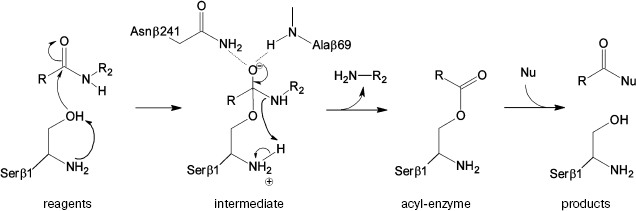
The prospective catalytic mechanism of Ntn-hydrolases can be described as follows (Fig. 1): first, the N-terminal serine hydroxyl is activated abstracting a proton by its own amino group. It was suggested that proton transfer could be mediated by a bridging water molecule [6]. Then activated serine attacks the carbonyl carbon of the substrate, leading to the formation of a tetrahedral intermediate. Negative charge on the carbonyl oxygen in the tetrahedral intermediate is stabilized by hydrogen bonding with the residues of the so-called oxyanion hole--the side chain amide of the Asnbeta241 and the backbone amide of Alabeta69. Also structural and kinetic data were derived suggesting the role of Argbeta263 in stabilization of the transition state [4, 10]. Decay of the unstable intermediate yields the acyl-enzyme complex via proton transfer to the leaving group of the substrate. In the deacylation reaction the same sequence of events occurs in reverse order: external nucleophile attacks the carbonyl carbon of the acyl-enzyme, which leads eventually to the acyl transfer product release.

Fig. 1. Suggested mechanism of PA catalysis.

However, the detailed catalytic mechanism of PA is still speculative and not supported by strict evidence. Moreover, some details seem ambiguous. Thus, it was shown [11] that the complex of the native enzyme with its “slow” substrate, penicillin-G-sulfoxide, possesses no water molecule located near Serbeta1 O^gamma. This fact contradicts the participation of a “bridge water molecule” in proton transfer from Serbeta1 to its own amino group. These facts and some other findings, in particular, ability of the enzyme to preserve its activity in acidic environment to pH 3.0 [12, 13], have raised additional questions concerning the unique catalytic mechanism of Ntn-hydrolases, suggesting the necessity of consideration at a strict theoretical level.

METHODS OF INVESTIGATION

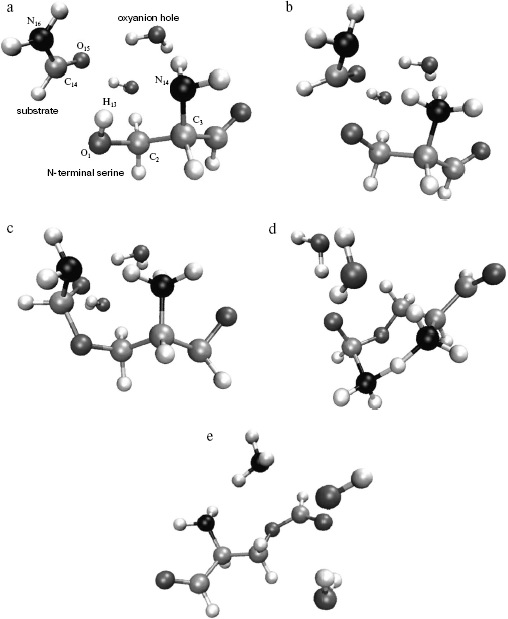
Model. For quantum chemical modeling of the catalytic mechanism of penicillin acylase, two molecular models--minimal and extended--were considered. The minimal model comprised formamide as a substrate, a serine molecule with free amino group, and an aldehyde group instead of carboxylic. The effect of specific solvation of the carboxyl oxygen of formamide was estimated in the extended model by two molecules of water (Fig. 2). The starting structures of molecular system were based on the X-ray structure of PA complex with its competitive inhibitor phenylacetic acid from Protein Data Bank (structure id 1PNL). Coordinates of serine atoms were transferred without any changes, formamide was superimposed with the carboxylic group of the inhibitor, and molecules of water (in the extended model) were placed in the direction of NH-groups of the main chain of Alabeta69 and the side chain of Asnbeta241--groups forming the enzyme oxyanion hole.

Fig. 2. Structures corresponding to stationary points of the potential energy surface of the extended model including substrate molecule (formamide), N-terminal serine analog (with its amide group replaced by aldehyde group), and oxyanion hole analog (two water molecules). a) Structure of the complex of reagents (analog of the enzyme-substrate complex); b) structure of the first transition state (TS1); c) structure of the tetrahedral intermediate; d) structure of the second transition state (TS2); e) structure of the products (acyl-enzyme analog).

Location of stationary points on a potential energy surface (PES). The starting point for the optimization of the reagents complex was prepared as described above. Starting points for location of other stationary configurations were prepared by empirical adjustments of chemical bond lengths to be formed or cleaved, and also by applying common knowledge from modeling similar systems [14-16].

Location of the stationary points (local minima and saddle points) was based on the Newton-Raphson algorithm [17] in the quadratic PES approximation (method QA in package PC Gamess [18]) with threshold value of the gradient 10^-4 a.u. First, optimization was conducted at the RHF/6-31+G** level. Further, full optimization was calculated at the MP2/6-31+G**//RHF/6-31+G** level.

For each of the located stationary points the eigenvalues of the second order derivatives matrix (Hessian) were calculated, and the character of a stationary point--a minimum or a transition state--was verified.

Following the intrinsic reaction coordinate. To check the belonging of the located stationary points to a single contiguous reaction pathway and to prove the absence of other stationary points on it, the so-called method of following the intrinsic reaction coordinate (IRC in package PC Gamess [19]) was used. For this purpose, a gradient descent on PES was carried out starting from the located transition states along both directions of the normal mode of imaginary frequency (negative eigenvalue of Hessian). The step size in the gradient descent was varied from of 0.01 to 0.1 (a.m.u.)^1/2 ·bohr depending on the steepness of the reaction pathway. This method was applied to points located at the RHF/6-31+G** level.

Account of nonspecific solvation. In addition to specific solvation (modeled by two water molecules), contribution from nonspecific solvation was estimated by the continuous polarizable environment model (method PCM in package PC Gamess) [20]. Water characteristics (dielectric permittivity, radius, surface tension, density, cavity size) were chosen to model the continuous environment. The contribution from solvation was calculated in each point obtained by the IRC method.

RESULTS AND DISCUSSION

Geometry of the stationary points. The following stationary points were located on the PES--complexes of reagents (formamide and serine), products (formyl-serine and ammonia), and tetrahedral intermediate corresponding to local minima--and also two transition states TS1 and TS2 (saddle points) separating reagents from intermediate, and intermediate from products, accordingly. The observed stationary points could be connected by a continuous curve of the steepest (gradient) descent on the PES, and thus they belonged to the single reaction pathway. These findings proved the idea of the suggested earlier mechanism of PA action (Fig. 1) according to which the amino group of the N-terminal serine residue is capable of activating its own hydroxyl.

Configurations of the located complexes are shown in Fig. 2 and basic geometric characteristics, such as interatomic distances and lengths of the bonds undergoing significant changes during the reaction, are presented in Table 1.

Table 1. Geometric characteristics of the stationary points in the extended model

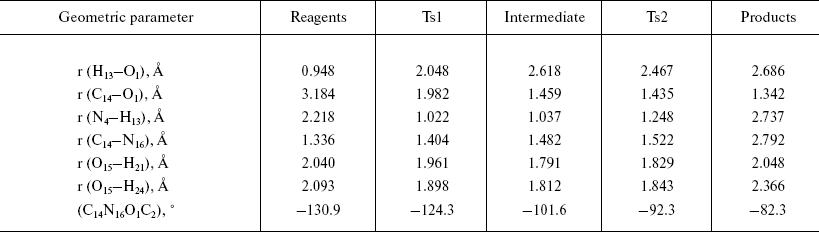
The optimized geometry of the reagents complex (Fig. 2a) was quite close to the corresponding atom arrangement in the X-ray structure 1PNL. In particular, the difference between the calculated value of the torsion angle determining side chain conformation of the serine and the X-ray data was 9.25°; orientation of the formamide relative to the serine was also in good agreement, with 4.8° difference between calculated and experimental values of the corresponding angle. The distance between the carbonyl carbon of the substrate and serine oxygen was 3.2 Å, which corresponded to the formation of a dense van der Waals contact between reagents at the stage of noncovalent complex formation. It is worth noting that the hydrogen atom of the serine hydroxyl group is oriented towards the free electron pair of the amino group (bond order equals 0.46), which apparently facilitates participation of the amino group during proton transfer at the rate-limiting stage of the reaction.

Formation of the first transition state (Fig. 2b) is characterized by complete proton transfer from the serine hydroxyl to its amino group (NH bond length 1.02 Å, bond order 0.606) and partial formation of a bond between the serine oxygen and the carbonyl carbon of the formamide (bond length 1.98 Å, bond order 0.669). Concretely, hybridization of the amide nitrogen of the formamide changed from sp2 to sp2.05, and interaction with solvent molecules strengthened as can be seen from the hydrogen bonds shortened from 2 to 1.9 Å.

Bond formation between the serine oxygen and the substrate carbon in the tetrahedral intermediate (Fig. 2c) is complete (bond length 1.46 Å). Hybridization of the formamide nitrogen (sp2.5) reminded rather amino compounds than amides, and the substrate oxygen lost carboxyl character (hybridization sp2.05, bond length 1.22 Å). Hydrogen bonds with two water molecules (bond length 1.8 Å) became shorter, and one more hydrogen bond between the charged amino group of Serbeta1 and formamide nitrogen (1.75 Å) was formed. The latter observations outline pre-organization of the molecular system in view of the subsequent events--proton transfer to the formamide nitrogen and release of ammonia.

In the last transition state, TS2 (Fig. 2d), the proton “is shared” between the leaving group (ammonia molecule) and the serine amino group (r (N₄-H₁₃) = 1.25 Å, r (N₁₆-H₁₃) = 1.61 Å; bond orders: 0.38 and 0.36, correspondingly). The carbonyl character of the oxygen atom O₁₅ becomes more pronounced (hybridization sp2.5, bond length 1.28 Å), and interaction with water molecules becomes weaker (r (O₁₅-H₂₁) = 1.829 Å, r (O₁₅-H₂₄) = 1.843 Å).

In the complex of products (Fig. 2e), a hydrogen bond between the ammonia molecule and the nitrogen of formyl-serine was present as well.

All in all, no significant changes along the reaction pathway were observed concerning the Serbeta1 conformation and the relative placement of water molecules modeling specific solvation. These observations suggest that the modeled chain of chemical transformations is compatible with highly structured spatial organization of the enzyme's active site.

Energy profile of the reaction. Analysis of the energy profile of the modeled reaction (Table 2) showed that the rate-limiting step of the formyl-serine (acyl-enzyme analog) formation was the transition from the complex of reagents (analog of Michaelis complex) to the tetrahedral intermediate. The energy barrier computed at the MP2/6-31+G** level was about 31 kcal/mol. However, the barrier separating products of the reaction from the corresponding intermediate was only 2.5 kcal/mol. It is known from published experimental data [10, 21] that acylation is the rate-limiting step of PA-catalyzed reactions. Corresponding rate constants for different substrates vary from 10 to 100 sec^-1. However, estimation of the deacylation (by water or other proper nucleophile) rate reveals values greater by an order of magnitude. Thus, comparison of the energy barrier calculated for the acylation step with the experimental value of activation energy is justified. However, the experimental value of 10 kcal/mol (obtained in Arrhenius approximation to the temperature dependence of the rate of enzyme reaction) is noticeably lower than theoretically calculated here. Apparently, this is caused by two major factors determining specific features of enzyme catalysis. First, it is multipoint and specific interaction between substrate and biomacromolecule that induces strain in enzyme-substrate complex and proper spatial arrangement of reagents, which is absent in non-condensed and isotropic (not specific) environments. Second, it is an opportunity to stabilize reaction transition state more effectively by more subtle and specific adjustment of interactions in the highly organized environment of the enzyme active center. Nevertheless, some important properties qualitatively characterizing specific details of enzyme catalysis can be assessed from a model system comprising just several molecules. Thus, account of specific solvation by means of two water molecules (in the extended model) revealed stabilization of the transition state by 10 kcal/mol compared to the minimal model. The contribution from nonspecific solvation by the method of polarizable continuum medium, due to certain technical problems, could be accounted for only in the RHF method, with electronic correlation neglected. Inclusion of the polarizable environment should account for the energetic contribution from interactions with the bulk of the molecular system (the enzyme). Contribution to the TS1 stabilization obtained by the RHF method was about 11 kcal/mol, and it was reasonable to expect that account of electronic correlation could further improve correspondence between theoretical and experimental values. It should be noted that calculated activation energy is in good agreement with experimental data obtained earlier for the reactions of nucleophile substitution at the carbonyl carbon proceeding via alternative mechanisms of general acid or base catalysis [22-24].

Table 2. Energetic characteristics of the stationary points in the extended model

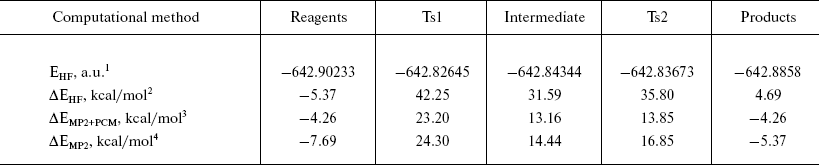
¹Absolute energy after optimization by RHF/6--31+G** method.
²Relative energy of the system compared to the geometric configuration corresponding to PDB structure 1PNL.
³Relative energy with account for electronic correlation (MP2) and interaction with solvent (PCM).
⁴Relative energy after optimization by MP2/6--31+G**.

In order to study the subtle aspects of enzyme specificity, there is a need to include into the model enzyme residues capable of stabilizing transition state by means of noncovalent interactions. Recent appearance of the so-called hybrid methods [25, 26] combining strict quantum chemical consideration of the active center of the enzyme, and more economic molecular-mechanical description of the rest of the system makes this possible. Such studies are currently being conducted in our laboratory.

This work was supported by the Russian Foundation for Basic Research (grant 06-04-49312).

REFERENCES

1.Kutzbach, C., and Rauenbusch, E. (1974) Hoppe Seyler's Z. Physiol. Chem., 354, 45-53.
2.Svedas, V. K., Margolin, A. L., Sherstiuk, S. F., Klyosov, A. A., and Berezin, I. V. (1977) Bioorg. Khim., 3, 546-553.
3.Brannigan, J. A., Dodson, G., Duggleby, H. J., Moody, P. C., Smith, J. L., Tomchick, D. R., and Murzin, A. G. (1995) Nature, 378, 416-419.
4.Done, S. H., Brannigan, J. A., Moody, P. C., and Hubbard, R. E. (1998) J. Mol. Biol., 284, 463-475.
5.Duggleby, H. J., Tolley, S. P., Hill, C. P., Dodson, G., and Moody, P. C. (1995) Nature, 373, 264-268.
6.Alkema, W. B. L., Hensgens, C. M., Kroezinga, E. H., de Vries, E., Floris R., van der Laan, J. M., Dijkstra, B. W., and Janssen, D. B. (2000) Protein Eng., 13, 857-863.
7.Oinonen, C., and Rouvinen, J. (2000) Protein. Sci., 9, 2329-2337.
8.Shewale, J. D., Deshpande, B. S., Sudhakaran, V. K., and Ambedkar, S. S. (1990) Process Biochem. Int., 25, 97-103.
9.Kasche, V., Lummer, K., Nurk, A., Piotraschke, E., Rieks, A., Stoeva, S., and Voelter, W. (1999) Biochim. Biophys. Acta, 1433, 76-86.
10.Morillas, M., Goble, M. L., and Virden, R. (1999) Biochem. J., 338, 235-239.
11.McVey, C. E., Walsh, M. A., Dodson, G. G., Wilson, K. S., and Brannigan, J. A. (2001) J. Mol. Biol., 313, 139-150.
12.Chilov, G. G., and Svedas, V. K. (2002) Can. J. Chem., 80, 699-707.
13.Chilov, G. G., Moody, H. M., Boesten, W. H. J., and Svedas, V. K. (2003) Tetrahedron: Asymmetry, 14, 2613-2617.
14.Diaz, N., Suares, D., and Sordo, T. L. (1999) J. Org. Chem., 64, 3281-3289.
15.Zhan, C.-G., Landry, D. W., and Ornstein, R. L. (2000) J. Am. Chem. Soc., 122, 2621-2627.
16.Pliego, J. R., Riveros, J. M., and Riveros, J. R., Jr. (2001) Chem. Eur. J., 7, 169-175.
17.Schlegel, H. B. (1987) Adv. Chem. Phys., 67, 249-286.
18.PC Gamess, http://classic.chem.msu.su/gran/gamess/index.html.
19.Ishida, K., Morokuma, K., and Komornicki, A. (1977) J. Chem. Phys., 66, 2153-2156.
20.Cammi, R., and Tomasi, J. (1995) Comput. Chem., 16, 1449-1458.
21.Alkema, W. B. L., Vries, E., Floris, R., and Janssen, D. B. (2003) Eur. J. Biochem., 270, 3675-3683.
22.Cassidy, C. S., Lin, J., and Frey, P. A. (1997) Biochemistry, 36, 4576-4584.
23.Hwang, J.-K., and Warshel, A. (1987) Biochemistry, 26, 2669-2673.
24.Molina, P. A., Sikorski, R. S., and Jensen, J. H. (2003) Theor. Chem. Acc., 109, 100-107.
25.Cramer, Ch. J., and Truhlar, D. G. (1999) Chem. Rev., 99, 2151-2200.
26.Zhang, Y., and Kua, J. (2002) J. Am. Chem. Soc., 124, 10572-10577.

---