REVIEW: Charge Motion during the Photocycle of Bacteriorhodopsin

A. Dér and L. Keszthelyi^*

Institute of Biophysics, Biological Research Center, Szeged, P.O.B. 521, Hungary, H-6701; fax: 36-62-433133; E-mail: derandra@nucleus.szbk.u-szeged.hu, kl@nucleus.szbk.u-szeged.hu

^* To whom correspondence should be addressed.

Received April 25, 2001; Revision received June 12, 2001

---

The function of bacteriorhodopsin in Halobacterium salinarum is to pump protons from the internal side of the plasma membrane to the external after light excitation, thereby building up electrochemical energy. This energy is transduced into biological energy forms. This review deals with one of the methods elaborated for recording the charge transfer inside the protein. In this method the current produced in oriented purple membrane containing bacteriorhodopsin is measured. It is shown that this method might be applied not only to correlate charge motion with the photocycle reactions but also for general problems like effect of water, electric field, and different ions and buffers for the functioning of proteins.

---

KEY WORDS: bacteriorhodopsin, photocycle, charge motion

Abbreviations: bR) bacteriorhodopsin; BTP) bis-tris propane; hR) halorhodopsin; PM) purple membrane; CP) cytoplasmic (side of the membrane); EC) extracellular (side of the membrane); ELMA (method)) method for orientation of the membranes applying ELectric and MAgnetic fields; FTIR) infrared spectroscopy with Fourier transformation.

The retinal containing protein bacteriorhodopsin (bR) is embedded in the plasma membrane of Halobacterium salinarum (formerly H. halobium). Its main function is to absorb light and use this energy for proton pumping from the cytoplasm to the extracellular medium. This way the absorbed light energy is transduced into electrochemical energy. The cell uses it to synthesize ATP.

After photon absorption the bR molecule undergoes a cyclic photoreaction with a transient all-trans to 13-cis isomerization of the retinal chromophore. Six intermediate states labeled J, K, L, M, N, and O with widely different lifetimes have been identified in this “photocycle” and were originally characterized by their absorption spectra [1]. During this process, cyclic changes occur in the protein. The changes can be classified into four cycles.

1. Charge motion cycle. We start with this because all other changes promote or indicate the charge motion. Conceived simply, there are at least two steps in getting the pumped proton through the bR molecule: uptake on the intracellular side and release at the extracellular side. Actually, it happens in more than two steps as discussed later.

2. Light absorption cycle. The first indication of the existence of a cycle was that the absorption maximum changed in time after absorption of a photon. Measurements performed at different wavelengths of the visible spectra have shown changes that served to characterize intermediates of the photocycle.

3. Retinal cycle. In the all-trans bR, the isomeric state of the retinal changes during the photocycle from all-trans to 13-cis and back.

4. Opsin cycle. Changes in the UV region indicate alterations in protein structure, because tyrosine and tryptophan residues absorb in this range. Data from infrared spectroscopy reflect changes in protonation of different aspartic acids as well as motions of the backbone of bR. Recently, in addition to the three dimensional structure of bR at 1.55 A resolution [2], structures of intermediates have also been obtained [3-6]. These data show the motions of backbone, amino acid side chains, and water molecules in more detail.

A working model of the bR function should harmonize with all data collected for the four cycles. Recent attempts in this direction may be found in [7-9].

In this review we concentrate on the charge motion cycle, the topic studied in more detail in our group. We try to correlate our findings with the other three cycles and also with the recent results on the structure of bR.

METHODOLOGY

Charge translocation by bR involves charge motion inside the molecule. Charges moving in a dielectric, in this case the membrane bound protein, induce displacement current which can be picked by properly constructed measuring systems. The essential requirement is to have orientation, i.e., that more than half of the proteins faces in one direction. In such cases the currents do not sum to zero.

Different methods are used for orientation based on the asymmetrically charged surfaces of the purple membrane (PM) containing the bR molecules. Because of the asymmetry the PM attach themselves to a bilayer, for example, by their extracellular surface [10, 11]. In other cases lipid impregnated filters [12] or a Teflon septum [13] support the asymmetrically adhering PM. These assemblages separate two compartments in a measuring cell. Electrodes are inserted into these compartments, which may have solutions of different composition. Under illumination, the charges will move in one direction and charge up the capacity of the system or may excite currents if the membrane is permeable for the pumped ions (being protons in the majority of cases). The capacitive or real current is registered.

The charge asymmetry on a purple membrane means that they possess a permanent electric dipole moment. The purple membrane fragments in a suspension are randomly oriented, but due to their permanent electric dipole moment they can be oriented by an electric field in such a way that they become ordered and faced in one direction. Electric field strength of 15-20 V/cm is enough to produce more or less complete orientation. This orientation stays as long as the field is on and decays after it is off. This relaxation takes 300-500 msec depending on the size of the PM and the viscosity of the medium [14].

The oriented purple membrane can be immobilized by two methods: 1) orienting them in an acrylamide solution (3-6% w/w) and then adding a polymerizing agent to it (the formation of a polyacrylamide gel containing mainly oriented purple membrane takes only 1 min [15]); 2) depositing the purple membrane on a glass plate covered with a transparent conducting layer (for example, SnO₂) by electrophoresis and drying it [16].

In the oriented purple membrane (either in a suspension or after immobilization), the charges move in one direction and are synchronized if the photocycle is excited by laser flash or quasi-continuous illumination (we call continuous illumination a few seconds long quasi-continuous). Moving charges create displacement current that is conducted from the purple membrane in the suspension to the electrodes. The time dependence of the signal can be measured.

The advantage of this method is that the number of the excited molecules is so large (10¹⁴ molecules may be easily excited with a laser flash) that light absorption measurements can be performed on the same sample that produces the electric signals. The single oriented layer in other methods practically excludes this possibility. This fact motivated further studies to improve the orientation.

In the ELMA (applying ELectric and MAgnetic fields) method the PM is first oriented with d.c. electric field and then a strong magnetic field (17 T) orients it further [17]. The method needs fine-tuning: a solution of increased viscosity keeps the electric orientation for the time needed to reach the high magnetic field. The solution also contains monomers that will be polymerized after the electric and magnetic orientation is established. This way the PM is immobilized. In successful cases the orientation can be increased three times.

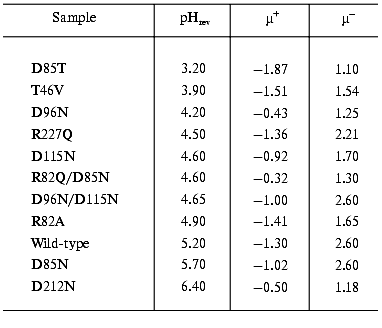
The study of the photocycle of bR mutants contributed greatly to understand the processes going on during the proton translocation. The electric responses are of special interest. To find optimal parameters for the necessary orientation we performed electrooptical measurements on PM containing different mutants of bR. The permanent electric dipole moment and polarizability of these membranes depends on pH [18]. It was already known that the sign of the permanent electric dipole moment changes at pH 5.2 in the case of PM with wild-type bR; consequently, the pH of the sample should be kept far from this pH_rev, better above it, during orientation. Table 1 contains data on pH_rev and the electric dipole moment µ for membrane containing different mutants.

Table 1. Values of pH_rev and the permanent electric dipole moment above (µ⁺) and below (µ^-) pH_rev (units of 10^-23 Cm per membrane)

PROTON TRANSFER AND PHOTOCYCLE

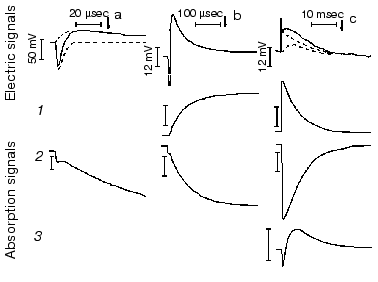
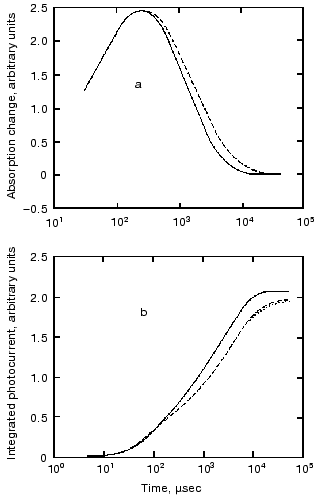
Protein electric response signal. A typical electric response signal in case of laser excited wild-type bR exhibits five time-resolved components as shown in Fig. 1 [14]. The first is a large, fast negative component, its decay time is determined by the measuring electric circuit, the second is a small negative component with 2 µsec lifetime (at room temperature), and it is followed by three positive components of 60 µsec, 8 msec and 2.2 msec lifetimes. The assignment of the sign of components is related to the direction of proton transfer: positive means positive charge motion from the cytoplasmic (CP) side to the extracellular (EC) side. The measured lifetimes coincided with the known lifetimes of the K, L, M and O intermediates of the photocycle [1]. Similar results were obtained later by Müller et al. [19]. It seemed straightforward to assign these components to charge motions during transitions between the intermediates. The amplitudes of the components also contained important information. Assuming that the photocycle is not-branching, unidirectional, only one proton moves and the dielectric inside the protein is homogeneous, we calculated the distances the protons take during each step. Table 2 contains these distances (we note that their sum was normalized to the thickness of PM). In spite of these assumptions and the simple theory used for evaluation (summarized in [20]), a reasonable interpretation based on early structural data [21] could be given to the distances. Namely, the major charge displacements occur during the millisecond part of the photocycle (M-O and O-bR transitions), corresponding to major proton movements between the intracellular side and the Schiff base and from the vicinity of the latter to the extracellular surface.

Fig. 1. Comparison of the electric and light absorption signals at different wavelengths: 408 (1), 522 (2), and 635 nm (3). a-c) Signals measured with different time resolution ((a) tens of microseconds, (b) hundreds of microseconds, (c) tens of milliseconds). Dashed lines in columns (a) and (c) denote the decomposition of the electric signals. The size of bars in absorption signals means a 10% change in absorption. Purple membrane in H₂O solution, orienting field 8.5 V/cm, temperature 20°C.

Table 2. Distances of the proton movements during the photocycle of bacteriorhodopsin estimated from the amplitude of the kinetic components of the electric signal (after [20])

^*Normalized to thickness of purple membrane.

Since that time a huge amount of data has been collected for wild-type bR and for its special mutants, analyzed with different photocycle models and compared to the more accurate three-dimensional structures of bR. These achievements lead to a new evaluation method of the electric response data combined with different photocycle model. Instead of distances the electrogenicity of the transitions was introduced [22-24]. The jth intermediate is characterized by the effective dipole magnitude:

where A is a normalizing factor,µ_ji are the dipole moments existing in the intermediate (for generality not only the displacement of the proton but other charged units are considered), and epsilon_ji is the dielectric constant of that section of the protein which surrounds the dipole. The electrogenicity of the intermediate is:

where D₀ is the ground state dipole magnitude. The electrogenicity changes during the transition from one intermediate to the other as their concentration changes. The generated electric current is:

    (1)

where the constant B is determined by the measuring circuit and C_j(t) is the concentration of the jth intermediate. Equation (1) is used to determine the electrogenicity of intermediates. The current has to be recorded and the C_j(t) values have to be determined. For this purpose, absorption kinetic measurements at different wavelengths and their evaluation are necessary. The normalizing constants A and B are not known. The usual method is to take the electrogenicity of the first, in general, not time-resolved signal, attributed to the primary charge separation, as a reference and to normalize the successive steps to it. The first signal in the case of wild-type bR is considered negative because it is opposite to the direction of proton translocation. Therefore it is taken as -1.

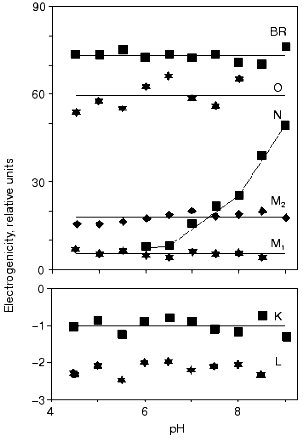
To achieve a reliable electric signal analysis the exact time constants and the time course of the concentration of intermediates have to be calculated. This is done by measuring absorption kinetics at different wavelengths. Each chosen wavelength is primarily characteristic for one of the intermediates of the photocycle. The current signal i(t) and its integral, the voltage u(t) are generated by the dipole changes occurring inside the membrane, during the whole photocycle. While the fast part of the signal is better characterized by the current signal, the slow charge motions, with much larger electrogenicities, give larger contribution to the integral. Therefore in a detailed study, measuring electrogenicities for wild-type bR in a broad pH range, the fitting procedure was performed on the voltage signals [24]. The result is presented in Fig. 2. We observe that electrogenicities of K and L intermediates are negative and small in the relative scale, while all the others are positive and much larger. They are pH independent except that of the N intermediate above pH 7. The transition through the N and O intermediates contains two major steps, the reprotonation of the Schiff base from Asp96 and the proton uptake step from the CP half channel of the membrane to Asp96 [25].

Fig. 2. The pH dependence of the electrogenicities of the intermediates. The horizontal lines are the average value of the corresponding electrogenicities. The error of calculations is less than ±15%.

The electrogenicity of intermediate O has a large positive value and is pH independent. At low pH, when no N, but much O is present in the photocycle, enough protons are still present to reprotonate Asp96 from the same distance and the rate limiting step is the reisomerization of the retinal. At high pH values, the reprotonation goes together with intermediate N and intermediate O kinetically disappears from the photocycle, indicating that the rate-limiting step is related to the proton translocation process. Around pH 6, both intermediates N and O are present in rather low concentrations. The fit of the N and O intermediates to the electric signal contains large error when their concentration is low (see the electrogenicity of O in Fig. 2). The very low electrogenicity of the intermediate N is compensated by a corresponding high value for O.

The electrogenicity of intermediate N seems to be pH dependent. Possibly, when the pH is increased the probability of taking up a proton from the surrounding decreases. The proton should come from a greater distance in the CP half channel. This suggests that there is not a well determined location of a proton donor for Asp96, but the conformational changes of the protein and the available free proton in the CP half channel modulate its accessibility. Another explanation of the pH dependency of the electrogenicity of intermediate N might be the fact that only one N intermediate was considered. It is known that two kinetically strongly overlapping N's exist with different protonation of the protein [25]. They may have different electrogenicities. By increasing the pH, the equilibrium between the two substates changes, resulting in a changing electrogenicity of the global N intermediate.

Similar electrogenicity measurements were performed on bR mutants D96N, D85N, and D212N [23, 26]. The cycle of 13-cis bR was also studied. The electric signal in this case also starts with a fast large negative signal as in the case of all-trans bR. An electric component corresponding to branching to the all-trans form was found too [27].

Very fast electric signal. The lifetime of the first electric response expected from absorption data is in the picosecond range. Conventional electric circuits are not applicable to measure so fast electric signals. To approach this time range, excitation with a picosecond laser and recording with a 30 GHz sampling oscilloscope were applied. In this early attempt the upper limit for the rise-time of the first response was found to be 30 psec [28]. Later, using a 170 fsec laser and 40 GHz sampling oscilloscope the forward (bR-K) and backward (K-bR) transitions were measured together [29]. The least square analysis of the recorded traces resulted in a 5 psec upper and 2.5 psec lower limit for the forward charge displacement process. The charge displacement driven by the backward transition was faster, having an upper limit of 3 psec. It is known that the first intermediate of the photocycle is the J intermediate appearing within 500 fsec and decaying to K within 5 psec. The 2.5 psec lower limit for the forward charge displacement seems to exclude charge motion connected to the bR-J transition. A much better time resolution, however, is desirable to confirm this result.

ELECTRIC SIGNALS IN THREE DIMENSIONS

Up to now, when speaking about electric signals, we tacitly understood them to be in the direction of the membrane normal. Although this is also the direction of the overall proton pumping, the charge displacements accompanying the photocycle are expected to have components parallel to the membrane plane, as well. The available methods, however, have long been unable to support the detection of such components, due to a rotational symmetry of the sample.

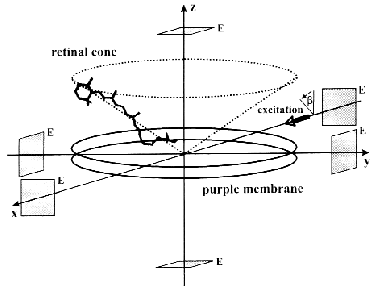
The ELMA technique, in combination with photoselective excitation, allowed us to measure the electric signals of bR in all the spatial dimensions [30]. The essence of the procedure is that the cylindrical symmetry of the system is broken by special photoselection. The sample of oriented PM is excited by low intensity light of appropriate linear polarization, so that bR molecules oriented in preferred directions are primarily excited (Fig. 3). Thus the in-plane components of the photocurrent can be determined. Figure 4 (a-c) shows traces detected in different spatial dimensions, I_x(t), I_y(t) and I_z(t), representing the Cartesian components of the photoelectric current measured on a sample containing PM oriented with the combination of electric and magnetic fields. As it was pointed out earlier [31], the time integral function of the photocurrent is proportional to the potential difference generated by the charge displacements during the pumping process, and it is properly scaled in terms of dipole moment changes accompanying the photocycle of bR molecules. Therefore, the integrated curves, U_x(t), U_y(t) and U_z(t) were considered in the subsequent analysis. A three-dimensional trajectory defined by the resulting dipole moment vector D(t) = [U_x(t),U_y(t),U_z(t)] in the first 400 µsec of the photocycle can be built.

Fig. 3. Geometry of a purple membrane oriented with its membrane normal coincident with the laboratory fixed z axis. The transition dipoles of individual retinal chromophores form a cone about this axis. The actinic laser pulse propagates along the laboratory fixed x axis with its polarization vector making an angle beta with the z axis. The rectangular symbols represent the measuring electrodes (E).

Fig. 4. Time-dependent photocurrents measured on PM oriented with the ELMA method, in the three perpendicular laboratory fixed spatial directions. The signals were picked up with electrode pairs oriented along the corresponding Cartesian axes: I_x(t) (a), I_y(t) (b), I_z(t) (c).

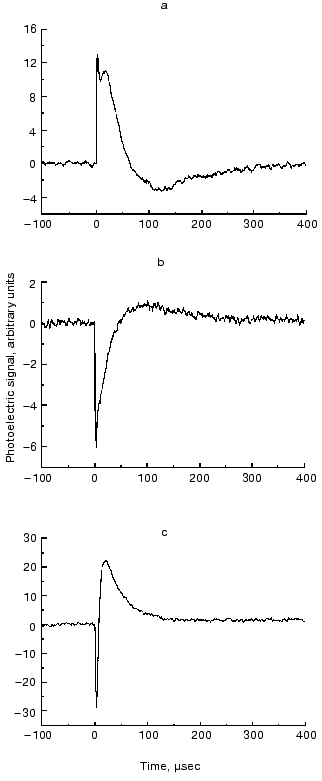
From the definition of the electric dipole moment it follows that this trajectory also characterizes the motion of the electric charge center of the bR molecules during the photocycle. For a single molecule, however, we assume a discrete stationary value for the dipole moment of an intermediate. The measured D(t) is a smooth function related to the whole sample, which always contains a mixture of intermediates. The corresponding µ_i values, therefore, can be determined if we know the time course of the concentration of the photocycle intermediates (c_i(t)) in the macroscopic sample. In order to determine the latter, absorption kinetics were measured on the same sample, under the same conditions, in addition to the photoelectric experiments.

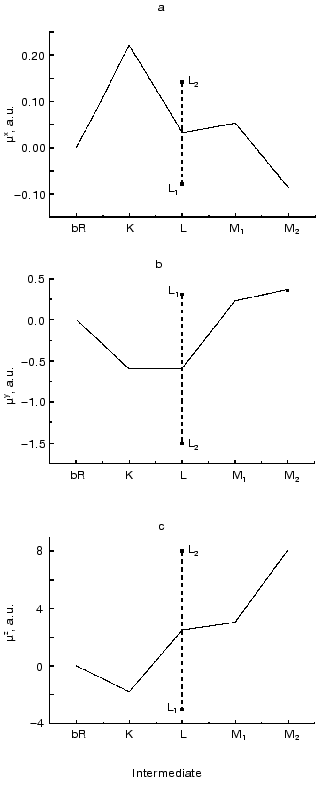
The absorption spectra of the K, L and M intermediates as well as the corresponding time dependent concentrations were determined according to [32], and the widely considered and tested photocycle model bR . K <--> L₁ <--> L₂ <--> M₁ <--> M₂ was used to calculate the intermediate concentrations up to 400 µsec. The result of a multilinear regression fit of D(t) with linear combinations of c_i(t) values yielded the µ_i values shown in Fig. 5 (a-c). As for the interpretation of the results in the molecular coordinate system, a positive µ_i^z corresponds to the displacement of a positive charge in the direction of the overall proton pumping. A positive µ_i^y results from the displacement of a positive charge parallel to the projection of the retinal transition dipole moment onto the membrane plane, roughly from helix E towards helix A. Finally, a positive µ_i^x corresponds to the displacement of a positive charge perpendicularly to both µ_i^y and µ_i^z, approximately from the direction of helix C to helix F.

Fig. 5. Dipole moment changes of the photocycle intermediates relative to the initial state obtained from three-dimensional photoelectric measurements. The individual dipole moments for the two L substates provided by our analysis were averaged to yield a single value comparable to the corresponding value from molecular dynamics calculations.

The experimentally determined µ_i^k values contain an undefined proportionality constant that is different in the three spatial directions. Consequently, the Cartesian components of a µ_i vector cannot be directly compared. However, the related µ_i^x, µ_i^y and µ_i^z components do contain important information about charge rearrangements inside the protein during the photocycle; therefore, their comparison with theoretically predicted data is of primary interest.

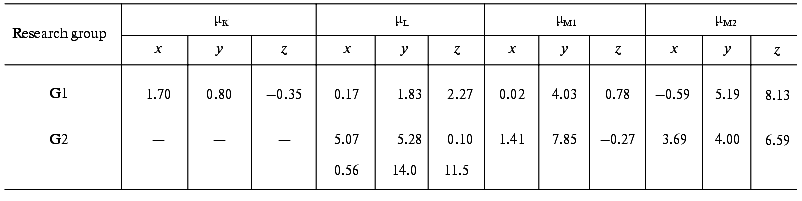
The later part of the photocycle still lies beyond the time window of traditional molecular dynamics theory. Based on the high resolution structure of bR determined by diffraction experiments, several attempts have been made using semiempirical or classical force field calculations and the method of simulated annealing, to compute the further progression of the photocycle [33-36]. Taking into account some known empirical parameters (pK values, FTIR data, etc.) and using plausible assumptions, structures for the L and M intermediates have also been published. We have calculated the µ_i values from two corresponding structures using the atomic coordinates and partial charge values, which include the surrounding water molecules in addition to the atoms of bR (personal communication by Professors Scharnagl and Schulten). Different molecular dynamics calculations yielded slightly different intermediate structures. Comparing the dipole moments (Table 3), one can conclude that the µ_i parameters represent a sensitive measure of these structural differences.

Table 3. Calculated electric dipole moment changes of the photocycle intermediates relative to bR from the molecular dynamics structures provided by two research groups: K. Schulten et al. (G1) and C. Scharnagl et al. (G2) (data from the latter group involve no K intermediate but two forms of L intermediate)

A detailed investigation regarding the assignment of components of the electric signal to rearrangements of particular charged and dipolar groups inside the bacteriorhodopsin molecule is in progress. Preliminary analysis suggests that, while proton motion makes a major contribution to the signals measured in the z direction, the signals measured in the x and y directions are apparently dominated by the reorientation and redistribution of water molecules.

These results imply that there is a good chance to find an improved theoretical model that could account for all the experimental results (including the observed charge displacements in the y direction), for which our method will provide the decisive test. Establishing such a model for the functional description of an ion pump protein at atomic level should have a strong impact on protein research in general.

NON-PROTON PUMPING

Bacteriorhodopsin in purple membrane near pH 2 shifts its absorption maximum from 568 to 605 nm forming the blue protein bR₆₀₅, which no longer transports protons, and shows no transient deprotonation of the Schiff base upon illumination [37, 38]. Continued acid titration with HCl or HBr but not H₂SO₄ restores the purple chromophore to yield bR₅₆₄(HCl) or bR₅₆₈(HBr) [39]. These acid purple forms also regain transmembrane charge transport (Fig. 6), but no transient Schiff base deprotonation is observed. (Here we would like to note that the late Dr. A. Kaulen and his coworker supported these results with independent experimental evidences gathered by another measuring technique [40].) In contrast to bR₅₆₈, no rate decrease of bR₅₆₄(HCl) transport kinetics is detected in ²H₂O, however, the transport rate decreases by a factor of ca. 2 in bR₅₆₈(HBr) compared with bR₅₆₄(HCl) [41]. The data indicated that in the acid purple form bR transports halide ions instead of protons. This conclusion is obviously important for understanding how bR functions and also interesting because the closely related halorhodopsin (hR) translocates halide ions at neutral pH.

Fig. 6. Quasi-stationary photocurrent signals of bR₆₀₅ (a) and bR₅₆₄ (b) at 24°C, pH 0.55 set by H₂SO₄ for bR₆₀₅ and HCl for bR₅₆₄. The curves depicted are the average of 64 traces. Arrow tips indicate timing of the first and the last laser pulse in the series. Transmission changes of bR₆₀₅ and bR₅₆₄ measured at 675 and 500 nm under the same conditions as the electric signals showed that stationary amplitude has been approximated to 90% within 30 msec (data not shown).

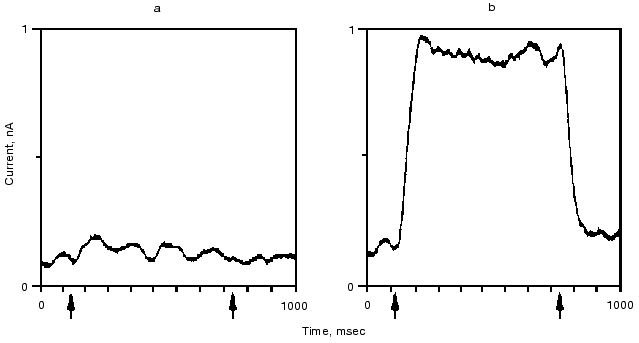
The retinal binding protein hR in the plasma membrane of Halobacterium salinarum functions as a light-driven Cl^- pump. It has a similar structure to bR and upon illumination undergoes similar absorption, retinal, and charge motion cycles. The first evidence for the latter was given in [42, 43]. In Fig. 7 we show the time dependence of the photoelectric signal. Correlation between the kinetics of electric and optical signals was established, and a “blue light effect” similar to that in bR was observed. Transient currents were observed both in the presence and the absence of Cl^-, net transport occurred only with Cl^- similarly to bR₅₆₄(HCl) [43].

Fig. 7. Photoelectric signal of hR measured at two different time resolutions: tens of microseconds (a) and tens of milliseconds (b). The sample was excited by 256 consecutive laser pulses (lambda = 575 nm; pulse length, 10 nsec; pulse energy, 1 mJ). Electrolyte composition: 100 mM NaCl, pH 6, 23°C.

A plausible model, based on the structure of bR and hR, was outlined to account for both types of transport in the two very similar proteins [41]. It explains how the essentially same retinal and opsin cycle and the same changes in local electric potential can move cations and anions in opposite directions. Minor changes in the protein affecting relative binding strengths and barrier heights can determine the pumping activity and which ion is transported. On the basis of the model we predicted that replacing Asp85 by a residue with a high pK OH^- group, e.g., threonine, which occupies the analogous position in hR, might allow Cl^- transport by bR at neutral pH. This has been shown to be the case [44].

ELECTRIC SIGNALS FROM INTERMEDIATES

The intermediates may also absorb photons and have their own photocycle ending in the ground state of bR. The study of the photocycle of the intermediates is important because it offers information on the photocycle of bR itself and because the behavior of bR under physiological conditions, i.e., under the continuous spectrum of the sunlight that excites the intermediates too, may be better understood [45]. Probably these are the reasons for the numerous reports dealing with photoexcitation of the intermediates (see review [46]). The majority of papers on excitation of intermediates deal with absorbance changes. The rather few studies of electric responses helped greatly in clarifying the intermediate photocycles.

The K intermediate absorbs at 610 nm. Its lifetime is 2 µsec at room temperature. In a study the oriented sample was cooled to liquid nitrogen temperature where its lifetime is extremely long. We could show that driving the photocycle forward with a green flash a fast negative signal appeared and a following red flash produced a positive electric signal of the same amplitude [47].

In the work for measuring the fast electric responses presented above [29] the femtoseconds laser ran with a repetition rate of 7 kHz and with wavelength of 620 nm that produced an equilibrium between bR and K. That way both lifetimes could be determined in the same measurement.

In the case of the L intermediate detailed studies have not yet been performed. The only existing data is that it begins with a fast positive component [48].

The best studied intermediate is M. In an experiment, continuous green light illumination of bR incorporated in a lipid bilayer produced current that could be decreased with additional blue light [45]. The authors correctly interpreted that illuminating M with blue light the photocycle was driven back to the ground state, i.e., proton translocation was interrupted. This effect is a photocycle regulator: the blue component of strong sunlight might diminish the activity of the photocycle. Working with flash light sources, it has been established that the M photocycle has two negative components [49]. Their amplitudes decrease with decreasing M population recorded as absorbance change. Summing the distances for motion in green and blue lights a zero distance was found.

The blue light effect has been used for different purposes. We mention three of them. In the case of the mutant D96N the presence of electrogenicity of the long-living component was checked illuminating the M intermediate with a blue flash and registering the known M response [50]. Dickopf and Heyn resolving the fast components of the M response in the nanosecond time range could discriminate between two M forms [48]. Similar results were found in another study but also compared to absorbance changes [51]. This latter paper contains information on M intermediate of mutants D96N and D85N too.

Much less is known about the electric signals associated with the late intermediates N and O. Published results exist only for the N intermediate of wild-type bR and mutant T46V [52]. N accumulates at high pH in case of wild-type bR and in mutant T46V, which has long living N component even at pH 7. With double flash experiments electric responses were found in both cases but their time-integral ended at zero, demonstrating that the N phototransformation did not involve charge translocation [52]. It turned out that the delay-time dependence of the electric signals is characterized by two distinct processes corresponding to two substates of the N intermediates postulated from absorbance measurements [25].

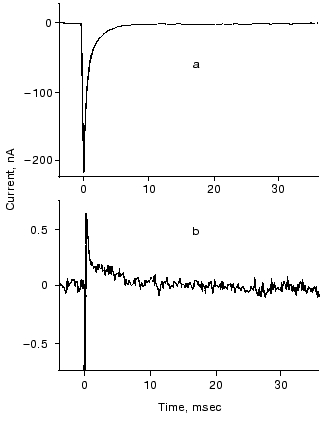
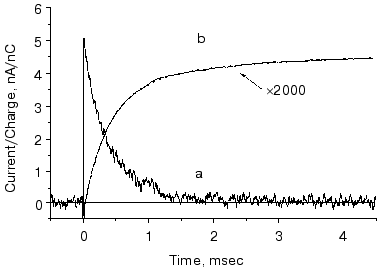
The O intermediate in wild-type bR accumulates at low pH (<5) and high temperature (~30°C). Experiments under these conditions provided evidences that the O photocycle of wild-type bR pumps protons too [53]. The time dependence of the current and translocated charge is shown in Fig. 8. The O intermediate of E204Q is different in that it does not pump protons.

Fig. 8. Electric signals for laser excitation (650 nm) of O of wild-type bacteriorhodopsin: a) current; b) time integral of the current.

The mutant L93A has a long living N intermediate in equilibrium with O [54]. The mutant has special features: O has 13-cis retinal, not all-trans as in wild-type bR (though even this is questioned [54]); the proton pumping activity in constant illumination of low intensity is small due to the very low turnover rate. The activity could be driven to approach that of wild-type bR in strong light. This latter characteristics is interpreted as a two-photon effect, i.e., that in strong constant light with broad spectrum the green components drive the photocycle to O and then the red components exciting O shortcut the cycle [54]. This way the turnover rate will increase.

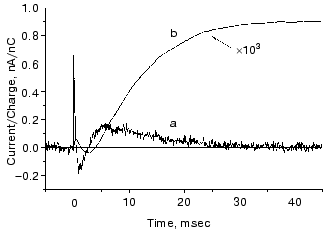
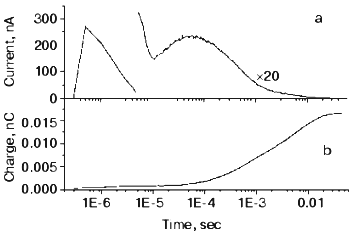
This mutant seemed well suited for studying the electric responses of the accumulated intermediates N and O. Using different techniques it was shown that the shortcut is in reality at N. It is known that in N the Schiff-base is reprotonated from Asp96, which is protonated again during the N-O transition. So, if there is a shortcut at N, a proton should move into the molecule from the cytoplasm to reestablish the ground state. This proton motion was really observed as shown in Fig. 9 [55]. The current is positive, in agreement with motion inward from the cytoplasmic side and its short lifetime (maximum 1.54 msec) harmonizes with a shortcut.

Fig. 9. a) Electric response due to the excitation of N intermediate in the case of mutant L93A; b) time-integral of the curve (a). The dashed line is the fit of curve (b) with two exponentials.

The O photocycle was also studied making use of the long lifetime. In this case the electric responses and measurement of proton release and uptake for the second flash at 650 nm, where O absorbs, provided evidence that the O photocycle is a proton pump [56]. Figure 10 depicts the time dependence of the current and translocated charge. It is interesting to note that the first fast signal is positive like in cases of K and L intermediates. The lifetime of O is ~140 msec, too long to accept its excitation as a shortcut.

Fig. 10. Electric response for laser excitation (650 nm) of O intermediate in the case of mutant L93A: a) time dependence of the current; b) its time integral.

APPLICATION FOR GENERAL PROBLEMS

The protein bR in PM is a simple system; its activity, after separation from cells, can be kept intact for a long time. Thus, bR is ideal for studying general problems of protein function, like effects of water, electric field, ions, and buffers.

Effect of water. It is well known that proteins can perform their function only if water is present. Water is necessary to keep the flexibility of proteins. In the case of bR the influence of water on the transitions between the different intermediates could be investigated.

The electric responses from dried oriented PM were studied in dependence of water content [16, 57]. The photocycle until M seemingly does not depend on water content. The deprotonated M is formed but the photocycle does not go beyond that intermediate at relative humidities below ~50%. The protons slowly return to the Schiff-base, performing an internal motion. Above this water content pumping is restored. These results are based on the time-integral (area) of the measured current being zero if pumping is absent and growing positive above 50% water content. The Arrhenius parameters of M decay also change abruptly at that water content. The O intermediate also appears, demonstrating its importance for pumping [57]. More details on the effect of water are found in references [58, 59]. Both papers, especially the second, compare absorbance changes and electric responses.

Effect of electric field. The activation enthalpy DeltaH and consequently the lifetime of a transition is effected in an external electric field [60]:

where V is the voltage on protein in the membrane of thickness D, d is the thickness of the barrier, i.e., the displacement of charge, F the Faraday constant, R the Boltzmann constant, and T the temperature. The measurement of the lifetime of transitions in externally applied electric field to PM is a possibility to determine the distance d the proton jumps between transitions.

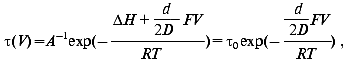
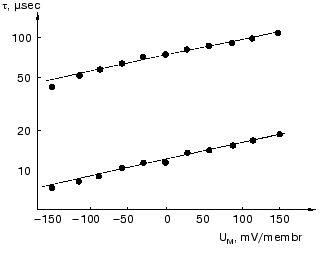
The dried oriented sample is ideal for such measurement. Figure 11 shows lifetime versus voltage data for the L-M transition [61]. The distance d obtained is 0.49 ± 0.02 nm, in good agreement with that in Table 2 for this transition.

Fig. 11. Voltage dependence of the lifetimes of the electric signals corresponding to the L-M transition in dried oriented samples. The two lines correspond to two components of the electric signals.

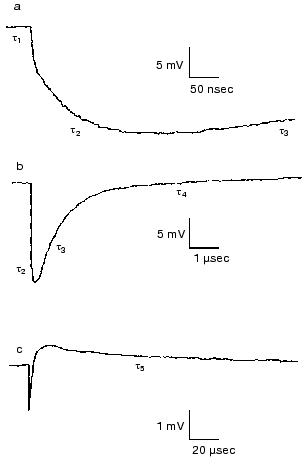
Effect of ions. Closer investigation of the rise of the first fast electric signal in solution after fast laser excitation indicated two kinetically distinct components, both temperature and ion concentration dependent [62]. Such signals are reproduced in Fig. 12. Though these signals were recorded in distilled water, extended measurements were performed in dependence of concentration of different monovalent and divalent ions [63]. In the nano- to microsecond region five lifetimes tau₁, tau₂, tau₃, tau₄ and tau₅ appear. The negative component with tau₄ is assigned to the K-L transition and the positive component with tau₅ to L-M transition. They do not depend on the ionic composition of the solution, only on temperature. The other three components, two in the rise and one in the decay, are the responses for the picosecond charge motion due to the bR-K transition (see section “Very fast electric signal”). The lifetime of decay tau₃ is due to the time constant (RC) of the input of the electronic circuit. If the resistance (R´) of the circuit is much larger than that of the solution, then R depends on the resistance of the solution, this way becoming ion-concentration dependent.

Fig. 12. Electric response signals from purple membrane oriented and immobilized in gel: a-c) signals with different amplitude and time scales ((a) tens of nanoseconds, (b) microseconds, (c) tens of microseconds). Distilled water suspension, temperature 22°C.

The real problem was to understand the components with lifetimes tau₁ and tau₂. The component tau₂ could also be resolved at temperatures above 0°C, tau₁ only below -80°C. Measuring ion-concentration and temperature dependence we found that the process with tau₁ can be assigned to conduction of electric current through H-bonds in ice and the process with tau₂ to diffusion of charges through the interfacial layer surrounding the PM [62].

The ratio of amplitudes of the two fast components remained a puzzle even after a very broad study performed in cases of different ions, concentrations, and temperatures [63]. It is surely connected with hitherto unknown peculiarities of the interfacial layer.

Ions surrounding purple membranes affect also the slower components of the electric signals. The effects of miscellaneous salts on the kinetics of absorption and photoelectric signals of bR at low ionic strength (<50 mM) have been attributed to changes in surface pH [64], buffer effects in the Gouy-Chapman layer (see next section), or cation binding to purple membranes [65]. Azide in millimolar concentrations is known to serve as a proton donor in certain bR mutants [66, 67], and high concentrations (>100 mM) of protonated azide have been recently shown to alter the photocycle kinetics and pathways of wild-type bR [68].

At moderate and high ionic strengths even neutral salts alter the millisecond phase of the photocycle via so-called Hofmeister interactions [69]. It was found that chaotropic thiocyanate ions accelerate the electric and absorption kinetic signals associated with the later part of the photocycle (Fig. 13). Bearing in mind that the major conformational changes accompanying the bR proton transport take place after the rise of the M intermediate, the observed acceleration of the photocycle was interpreted as a consequence of conformational destabilization by the chaotropic anions.

Fig. 13. Photocycle kinetics of bacteriorhodopsin in the presence of extremely chaotropic (SCN^-, solid line), polar kosmotropic (F^-, dashed and dotted lines), and Hofmeister-neutral (Cl^-, dashed line) anions at 25°C, pH 7.0. The result for acetate (kosmotropic) coincided with the chloride curve. a) Absorption monitored at 400 nm; b) photoelectric signals.

Effect of buffers. Buffers change the electric signals of light-excited bacteriorhodopsin molecules in purple membrane if their concentration and the pH of low salt solution are properly selected. We found that diamines reverse the current without changing the parameters of the photocycle [70, 71]. Later it turned out that there are “positive” buffers producing a positive component, and “negative” buffers producing a negative component additional to the signals due to proton pumping [72]. We set out to acquire more information on this important problem by studying the effects of buffers on the electric signals. We therefore selected a “positive” buffer (glycyl-glycine, Gly-Gly) and a “negative” buffer (bis-tris propane, BTP) and measured not only the components in the time range below millisecond, but all other components of the electric signals. We also determined the temperature dependencies of the rate constants not dealt with in [72].

Measurement of the buffer effects in the presence of Gly-Gly or BTP revealed an increase of ~2 and a change of sign and decrease to ~-0.5 in the translocated charge in these cases, respectively. These factors do not depend on temperature. The Arrhenius parameters established from the evaluation of the kinetics indicate activation enthalpies of 35-40 kJ/mol and negative activation entropies for the additional signals [73]. These values agree with those found by surface bound pH sensitive probes in the search of the timing of proton release and uptake [74, 75]. These authors assigned the probe signal to protons dwelling in the surface layer and migrating from the EC side to the cytoplasmic side. A unified explanation for the data obtained with surface bound probes and electric signals based on the clusters at EC and cytoplasmic sites of bacteriorhodopsin participating in proton release and uptake is as follows.

Recent studies with mutants assume that the proton release and uptake may occur in clusters at the EC side (Glu194, Glu204, and water molecules), and at the CP side (Arg227 and Asp38), respectively. We hypothesize that the proton release from the EC cluster and the uptake at the CP cluster involve reorganizations of the participant residues and water molecules. The protonation of amino acid Asp85 creates an electric dipole that induces ordering in EC and CP clusters (rise of the probe signal) to conformations able to release (EC side) or uptake and relay proton (CP side) in a second conformation change (decay of the probe signal). These reactions take place far from the neighborhood of the retinal, and therefore they do not influence the light-absorption signals, i.e., they are silent in the visible but may appear in the infrared. The processes have different activation enthalpy from the known values occurring in the photocycle and, as ordering phenomena, they have the characteristic negative entropy. These Arrhenius parameters, which should characterize the proton release and relaying, are measured with the proton sensitive probes at the two sides of the PM. This way, we assign the phenomena characterized with the probe signals to the bR molecule itself and not to surface properties. The probes are protonated as the protein releases the protons from the cluster at the EC side or as they are approaching the CP cluster. We assume that in the latter process the probe gets protonated first due to reorganization of the CP cluster and then transfers the proton to one of the members of the cluster. This hypothesis is an alternative interpretation of the probe data. However, it goes further by assigning the measured and not yet explained Arrhenius parameters to these processes.

The additional electric signals seemingly reflect the processes in the clusters if the buffers are added in appropriate concentration, salt, and pH. The coincidence of the Arrhenius parameters of the additional electric signals with those measured with the proton sensitive probe lead us to generalize the hypothesis and argue that the interaction of the clusters and buffers are responsible also for the additional currents.

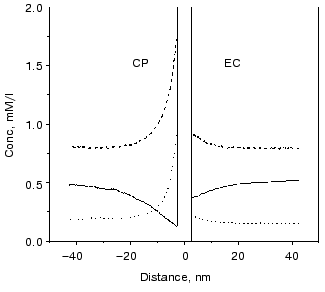
The surface charge asymmetry of PM, a four-charge difference between the CP and EC side, establishes an uneven microdistribution of the charged buffers in a more or less salt-free solution. At the pH of “good efficiency”, i.e., at which the additional charge motion is high, the charge states of buffers are shifted in the direction of deprotonation. Therefore, there are negatively charged Gly-Gly molecules, and singly and doubly positively charged BTP molecules in the solutions. Figure 14 shows that concentration gradients of the charged buffers build up around the PM. The main difference in the microdistribution of these buffers in addition to the uneven gradients at the two sides is that the positively charged BTP buffer molecules are much nearer to the membrane than the negatively charged Gly-Gly buffer molecules and the direction of the concentration gradient is opposite.

Fig. 14. Calculated microdistribution of the charged buffers around PM. Solid line, singly charged Gly-Gly; dashed line, singly charged BTP; dotted line, doubly charged BTP. Conditions: one negative charge at the EC surface, five negative charges at the CP surface per bacteriorhodopsin molecule, pH 7.5.

The difference between a buffered and a buffer-free solution, therefore, resides in the uneven, non-homogeneous microdistribution of the buffers determined by the surface charges of the PM. It is very important to note that buffers are special proton donors and acceptors. The buffers can efficiently take the protons away from the site or toward the site of reactions.

The cases of Gly-Gly and BTP buffer need different treatments. First we deal with the Gly-Gly buffer. As the protons are released from the EC cluster they are picked up by the buffers and guided along the concentration gradient of the negatively charged Gly-Gly molecules shown in Fig. 14. This proton motion is directed perpendicularly to the surface of PM and produces the EC part of the current. At the CP side protons are picked up by the CP cluster from the neutral buffers that become negative and are driven away from the membrane. This process occurs in the microsecond time domain controlled by the reorganization of the cluster as mentioned above. Motion of positive charge at the EC side and negative in opposite direction at the CP side induces the observed positive additional current.

In the case of the BTP buffer the additional current has microsecond and millisecond components. The Arrhenius parameters of the microsecond component are in the usual range with negative entropy, while the millisecond component has large activation enthalpy and positive activation entropy. The proton released from the cluster at the EC side diffuses to some distance and then a singly positively charged BTP molecule picks it up and now, being doubly charged, moves to the membrane, generating negative current. This process is responsible for the microsecond components of the additional current. At the CP side protons are picked up preferentially from the doubly charged buffers and, as singly charged molecules, they move away from the membrane, again generating negative current. This process is responsible for the long living component.

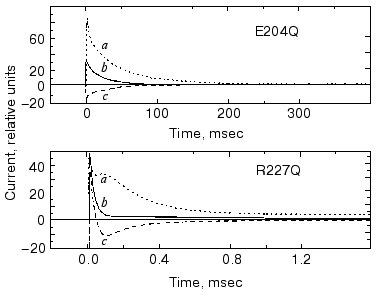
It seemed obvious to study the buffer effects on PM containing bR mutants with exchanged amino acids in the release or uptake clusters and also on delipidated PM containing wild-type bR. In Fig. 15 we show the change in current under laser flash illumination for mutants R227Q and E204Q. The mutant R227Q and other mutants with changed amino acids in the uptake cluster behaved like the wild-type bR, but the response in case of E204Q with changed release cluster was different. The response in case of delipidated PM containing wild-type bR did not deviate from that measured in case of normal PM, demonstrating that the additional current originated in bR itself. In the case of non-pumping mutants additional charge transfer was not found. Thus, the results with mutants are in agreement with the cluster hypothesis and also substantiate it [76].

Fig. 15. Current upon laser illumination in the case of mutants E204Q and R227Q measured in the presence of Gly-Gly (a) and BTP (c) buffers and without buffers (b). Buffer concentrations: 5 mM Gly-Gly, 1 mM BTP, respectively, pH 7.5, temperature 24°C (note the different time scales).

The results for internal charge motion in bacteriorhodopsin surveyed in this review have been obtained mainly with one method applied in our laboratory. As mentioned above, other powerful methods have also been elaborated [10-13]. All these studies piled up a great wealth of information. We believe that a comparative summary of all these results could illuminate many important aspects of charge transport by bacteriorhodopsin. It is regretful that one of the pioneers of these studies, Dr. A. Kaulen, cannot participate in that hypothetical endeavor.

We are thankful for the arduous work of all colleagues who participated in the reviewed studies in our laboratory. They are mentioned as authors of the publications. Special thanks are due to Drs. Zs. Dancsházy, G. Váró, and L. Oroszi for their help during writing this paper. This work was supported by the Hungarian National Science Fund OTKA T025236 and T029814.

REFERENCES

1.Lozier, R. H., Bogomolni, R. A., and Stoeckenius, W. (1975) Biophys. J., 15, 955-963.
2.Luecke, H., Schobert, B., Richter, H. T., Cartellier, J. P., and Lanyi, J. K. (1999) J. Mol. Biol., 291, 809-911.
3.Luecke, H., Schobert, B., Richter, H. T., Cartellier, J. P., and Lanyi, J. K. (1999) Science, 286, 255-260.
4.Royant, A., Edman, K., Ursby, T., Pebay-Peyroula, E., Landau, E. M., and Neutze, R. (2000) Nature, 406, 645-648.
5.Sass, H. J., Büldt, G., Gessenich, R., Hehn, D., Neff, D., Schlesinger, R., Berendzen, J., and Ormos, P. (2000) Nature, 406, 649-653.
6.Subramanian, S., and Henderson, R. (2000) Nature, 406, 653-656.
7.Lanyi, J. K. (2000) J. Phys. Chem., 104, 11441-11448.
8.Oesterhelt, D. (1998) Curr. Opin. Struct. Biol., 8, 489-500.
9.Stoeckenius, W. (1999) Protein Science, 8, 447-459.
10.Dancsházy, Zs., and Karvaly, B. (1976) FEBS Lett., 72, 136-138.
11.Bamberg, E., Dencher, N. A., Fahr, A., and Heyn, M. P. (1981) Proc. Natl. Acad. Sci. USA, 78, 7702-7706.
12.Drachev, L. A., Kaulen, A. D., and Skulachev, V. P. (1978) FEBS Lett., 87, 161-167.
13.Moltke, S., and Heyn, M. P. (1995) Biophys. J., 69, 2066-2073.
14.Keszthelyi, L., and Ormos, P. (1980) FEBS Lett., 109, 189-193.
15.Dér, A., Hargittai, P., and Simon, J. (1985) J. Biochem. Biophys. Meth., 10, 295-300.
16.Váró, G., and Keszthelyi, L. (1983) Biophys. J., 43, 47-51.
17.Dér, A., Tóth-Boconádi, R., Keszthelyi, L., Kramer, H., and Stoeckenius, W. (1995) FEBS Lett., 377, 419-420.
18.Mostafa, H. I. A., Váró, G., Tóth-Boconádi, R., Dér, A., and Keszthelyi, L. (1996) Bophys. J., 70, 466-472.
19.Müller, K. H., Butt, H.-J., Bamberg, E., Fendler, K., Hess, B., Siebert, F., and Engelhardt, M. (1991) Eur. J. Biophys., 19, 241-251.
20.Keszthelyi, L., and Ormos, P. (1989) J. Membr. Biol., 109, 193-200.
21.Henderson, R., Baldwin, J. M., Ceska, T. A., Zemlin, F., Beckmann, E., and Downing, K. H. (1990) J. Mol. Biol., 213, 899-929.
22.Trissl, H. W. (1990) Photochem. Photobiol., 51, 793-818.
23.Gergely, Cs., Ganea, C., Száraz, S., and Váró, G. (1995) J. Photochem. Photobiol. B: Biol., 27, 27-32.
24.Ludmann, K., Gergely, Cs., Dér, A., and Váró, G. (1998) Biophys. J., 75, 3120-3126.
25.Zimányi, L., Cao, Y., Needleman, R., Ottolenghi, M., and Lanyi, J. K. (1993) Biochemistry, 32, 7669-7678.
26.Gergely, Cs., Ganea, C., Groma, G. I., and Váró, G. (1993) Biophys. J., 65, 2478-2483.
27.Gergely, Cs., Ganea, C., and Váró, G. (1994) Biophys. J., 67, 855-861.
28.Groma, G. I., Szabó, G., and Váró, G. (1984) Nature, 308, 557-558.
29.Groma, G. I., Hebling, J., Ludwig, C., and Kuhl, J. (1995) Biophys. J., 69, 2060-2065.
30.Dér, A., Oroszi, L., Kulcsár, Á., Zimányi, L., Tóth-Boconádi, R., Keszthelyi, L., Stoeckenius, W., and Ormos, P. (1999) Proc. Natl. Acad. Sci. USA, 96, 2776-2781.
31.Dér, A., Tóth-Boconádi, R., and Száraz, S. (1992) Colloque INSERM, 221, 197-200.
32.Gergely, Cs., Zimányi, L., and Váró, G. (1997) J. Phys. Chem., 101, 9390-9395.
33.Humphrey, W., Xu, D., Sheves, M., and Schulten, K. (1995) J. Phys. Chem., 99, 14549-14560.
34.Xu, D., Sheves, M., and Schulten, K. (1995) Biophys. J., 69, 2745-2760.
35.Scharnagl, C., Hettenkofer, J., and Fischer, S. F. (1994) Int. J. Quantum Chem., 21, 33-56.
36.Engels, M., Gerwert, K., and Bashford, D. (1995) Biophys. Chem., 56, 95-104.
37.Mowery, P. C., Lozier, R. H., Chae, Q., Tseng, Y.-W., Taylor, M., and Stoeckenius, W. (1979) Biochemistry, 18, 4100-4107.
38.Dér, A., Tóth-Boconádi, R., and Keszthelyi, L. (1989) FEBS Lett., 259, 24-26.
39.Keszthelyi, L., Száraz, S., Dér, A., and Stoeckenius, W. (1990) Biochim. Biophys. Acta, 1018, 260-262.
40.Kalaidzidis, I. V., and Kaulen, A. D. (1997) FEBS Lett., 418,239-242.
41.Dér, A., Száraz, S., Tóth-Boconádi, R., Tokaji, Zs., Keszthelyi, L., and Stoeckenius, W. (1991) Proc. Natl. Acad. Sci. USA, 88, 4751-4755.
42.Dér, A., Fendler, K., Keszthelyi, L., and Bamberg, E. (1985) FEBS Lett., 187, 233-236.
43.Dér, A., Száraz, S., and Keszthelyi, L. (1992) J. Photochem. Photobiol., 15, 299-306.
44.Sasaki, J., Brown, L. S., Chon, Y.-S., Kandori, H., Maeda, A., Needleman, R., and Lanyi, J. K. (1995) Science, 269, 73-75.
45.Karvaly, B., and Dancsházy, Zs. (1977) FEBS Lett., 76, 36-40.
46.Balashov, S. P. (1995) Isr. J. Chem., 35, 415-428.
47.Ormos, P., Reinisch, L., and Keszthelyi, L. (1982) Biochim. Biophys. Acta, 732, 471-479.
48.Dickopf, S., and Heyn, M. P. (1997) Biophys. J., 73, 3171-3181.
49.Ormos, P., Dancsházy, Zs., and Keszthelyi, L. (1980) Biophys. J., 31, 207-213.
50.Butt, H.-J., Fendler, K., Bamberg, E., Tittor, J., and Oesterhelt, D. (1989) EMBO J., 8, 1657-1663.
51.Ludmann, K., Ganea, C., and Váró, G. (1999) J. Photochem. Photobiol. B. Biol., 49, 23-28.
52.Tóth-Boconádi, R., Szabó-Nagy, A., Taneva, S. G., and Keszthelyi, L. (1999) FEBS Lett., 499, 5-8.
53.Tóth-Boconádi, R., Taneva, S. G., and Keszthelyi, L. (2001) J. Biol. Phys. Chem., in press.
54.Delaney, J. K., Schweiger, U., and Subramaniam, S. (1995) Proc. Natl. Acad. Sci. USA, 92, 11120-11124.
55.Tóth-Boconádi, R., Keszthelyi, L., and Stoeckenius, W. (2001) Biophys. J., submitted.
56.Tóth-Boconádi, R., Keszthelyi, L., and Stoeckenius, W. (2001) Biophys. J., submitted.
57.Váró, G., and Keszthelyi, L. (1985) Biophys. J., 47, 243-246.
58.Kovács, I., and Váró, G. (1988) J. Photochem. Photobiol. B. Biol., 1, 469-474.
59.Groma, G., Kelemen, L., Kulcsár, Á., Lakatos, M., and Váró, G. (2001) Biophys. J., in press.
60.Zwolinsky, H. P., Eyring, H., and Reece, C. E. (1949) J. Phys. Chem., 53, 1426-1449.
61.Groma, G. I., Váró, G., and Keszthelyi, L. (1988) in Molecular Physiology of Retinal Proteins (Hara, T., ed.) Yamada Science Foundation, Japan, pp. 97-101.
62.Dioumaev, A. K., Chernavskii, D. S., Ormos, P., Váró, G., and Keszthelyi, L. (1992) Biophys. J., 61, 1194-1200.
63.Mostafa, H. I. A. (1996) Fine Structure of the Fast Electric Signal of Bacteriorhodopsin: Candidate's dissertation, Hungarian Academy of Sciences.
64.Ebrey, T. G. (1993) in Thermodynamics of Membranes, Receptors and Channels (Jackson, M., and Meyer, B., eds.) CRC Press, Orlando, FL, pp. 353-386.
65.Szundi, I., and Stoeckenius, W. (1987) Proc. Natl. Acad. Sci. USA, 84, 3681-3684.
66.Tittor, J., Soell, C., Oesterhelt, D., Butt H.-J., and Bamberg, E. (1989) EMBO J., 8, 3477-3482.
67.Otto, H., Marti, T., Holz, M., Mogi, T., Lindau, M., Khorana, H. G., and Heyn, M. P. (1989) Proc. Natl. Acad. Sci. USA, 86, 9228-9232.
68.Ormos, P., Dér, A., Gergely, Cs., Kruska, S., Száraz, S., and Tokaji, Zs. (1997) J. Photochem. Photobiol., 40, 111-115.
69.Dér, A. and Ramsden, J. J. (1998) Naturwissenschaften, 85, 353-355.
70.Tóth-Boconádi, R., Hristova, S. G., and Keszthelyi, L. (1986) FEBS Lett., 195, 164-168.
71.Dér, A., Tóth-Boconádi, R., and Keszthelyi, L. (1988) FEBS Lett., 229, 313-316.
72.Liu, S. Y., Kono, M., and Ebrey, T. G. (1991) Biophys. J., 60, 204-216.
73.Tóth-Boconádi, R., Dér, A., and Keszthelyi, L. (2000) Biophys. J., 78, 3170-3177.
74.Heberle, J., and Dencher, N. A. (1992) Proc. Natl. Acad. Sci. USA, 89, 5996-6000.
75.Heberle, J., Riesle, J., Thiedemann, G., Oesterhelt, D., and Dencher, N. A. (1994) Nature, 379, 379-382.
76.Tóth-Boconádi, R., Dér, A., Taneva, S. G., Tuparev, N., and Keszthelyi, L. (2001) Eur. J. Biophys., 30, 140-146.

---