New Approach to Analysis of Deviations from Hyperbolic Law in Enzyme Kinetics
B. I. Kurganov
Bach Institute of Biochemistry, Russian Academy of Sciences, Leninskii pr. 33, Moscow, 117071 Russia; fax: (095) 954-2732; E-mail: kurganov@gagarinclub.ru
Received February 10, 2000
An empirical equation that describes deviations from Michaelian kinetics is proposed. The equation allows the limiting values of the Michaelis constant at v/Vmax --> 0 and v/Vmax --> 1 to be estimated (v is the rate of the enzymatic reaction and Vmax is the limiting value of v at saturating concentrations of substrate). The applicability of the equation is demonstrated for kinetic data obtained for glutamate dehydrogenases from various sources (negative kinetic cooperativity for coenzyme) and for biosynthetic threonine deaminase from pea seedlings (sharper approaching the limiting value of the enzymatic reaction rate with increasing substrate concentration in comparison with the hyperbolic law). The negative cooperativity for the function of saturation of protein by ligand is also analyzed (data on binding of spin-labeled NAD, NADH, and NADPH by beef liver glutamate dehydrogenase and binding of cupric ions by BSA are used as examples).
KEY WORDS: enzyme kinetics, allosteric enzymes, negative cooperativity, glutamate dehydrogenase, biosynthetic threonine deaminase, NAD, NADH, NADPH
Deviations from the hyperbolic law for the dependences of enzymatic reaction rate on substrate concentration are of frequent occurrence in enzyme kinetics [1]. They can be connected with a complicated mechanism of the enzymatic process (especially in the case of multisubstrate enzyme reactions), non-equivalency of substrate-binding sites or interactions between substrate-binding sites in the molecule of an oligomeric enzyme, and the occurrence of enzymic forms (including oligomeric forms) differing in their catalytic properties in the enzyme preparation ([2], pp. 32-54). In order to interpret the deviations from Michaelian kinetics, experimenters, apart from the different kinetic approaches, should use physical and physicochemical methods providing control of conformational and oligomeric state of the enzyme at different stages of the enzymatic process. The experimenter often has great difficulty in choosing between the mechanisms that are proposed for explanation of the kinetic anomalies under observation. Therefore, empirical equations designed for description of the dependence of the enzymatic reaction rate (v) on the substrate concentration (S) remain popular. These equations are used for general characterization of the shape of the dependence of v on [S]. The Hill equation is very popular. In order to explain the appearance of the Hill equation, we start from the well-known Michaelis-Menten equation:
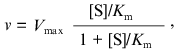 (1)
(1)where v is the steady-state rate of the enzymatic reaction, [S] is the initial concentration of the substrate, Vmax is the limiting value of v at saturating concentrations of the substrate (i.e., at [S] --> infinity), and Km is the Michaelis constant. In order to describe the deviations from the hyperbolic law, the Michaelis constant can be considered as an effective constant (Kmeff), which is a power function of the substrate concentration:
where K and n are constants. Application of this assumption leads to the Hill equation:
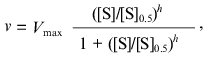 (3)
(3)where [S]0.5 is the “semisaturation” concentration, i.e., the substrate concentration at which v = Vmax/2, and h is the Hill coefficient. At h = 1 this equation is transformed into the classic Michaelis-Menten equation, [S]0.5 corresponding to the Michaelis constant Km. The case when h > 1 corresponds to the S-shaped dependences of v on [S], whereas the case when h < 1 corresponds to the dependences of v on [S] with delayed approaching the limiting value of the enzymatic reaction rate (Vmax) with increasing substrate concentration. Among three parameters of the Hill equation (Vmax, [S]0.5, and h), only parameter Vmax has clear physical meaning. The other two parameters are used for characterization of the shape of the v versus [S] curve: parameter [S]0.5 characterizes the position of the point at which v = Vmax/2 on the abscissa axis, whereas parameter h characterizes the slope of the straight line in coordinates {log[v/(Vmax - v)]; log[S]}. From comparison of Eqs. (2) and (3) it follows that
The chief disadvantage of the Hill equation is that the equation does not allow the values of the Michaelis constant at low and high substrate concentrations to be estimated. Actually, it is seen from Eq. (2) that at [S] --> 0 the Kmeff value approaches zero and at [S] --> infinity the Kmeff value tends to infinity. However, it is evident that finite values of Km should exist at [S] --> 0 and [S] --> infinity. Thus, the Hill equation can be used only for description of the central region of the values of v/Vmax (i.e., the values of v/Vmax near 0.5).
It is of special interest to go from the Hill equation to equations that would allow us to make estimates of the limiting values of Km at [S] --> 0 and [S] --> infinity. Ainsworth [3, 4] proposed that the effective Michaelis constant Kmeff is an exponential function of the v/Vmax ratio:
where K0 and Klim are the values of Kmeff at v/Vmax --> 0 and v/Vmax --> 1, respectively. The dependence of v on [S] has the following from:
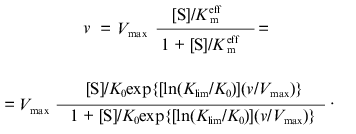 (5)
(5)In contrast to the Hill equation, all the parameters of the Ainsworth equation (Vmax, K0, and Klim) have clear physical meaning. However, in spite of the attractiveness of Eq. (5), the analysis of the data presented in [3] showed that this equation was not fulfilled in the regions of v/Vmax close to zero and unity. Therefore, parameters K0 and Klim calculated from the description of the central part of the dependence of v on [S] (i.e., the region of the v/Vmax values close to 0.5) can not be interpreted as the values of the Michaelis constant at v/Vmax --> 0 and v/Vmax --> 1, respectively. Thus, from the practical point of view the Ainsworth equation has no advantages over the Hill equation.
In the present work a new empirical equation for the dependence of v on [S] is proposed. In certain cases the equation allows the limiting values of the Michaelis constant at relatively low and relatively high concentrations of the substrate to be estimated. The equation proposed is applicable also for description of negative cooperativity for the functions of saturation of protein by ligand.
CALCULATING PROCEDURE
All the calculations in the present paper were carried out using the program Scientist (MicroMath, Inc., USA). In order to characterize the degree of agreement between the experimental data and calculated values, we used the determination coefficient R2 (without considering the statistical weight of the results of measurements) [5]:
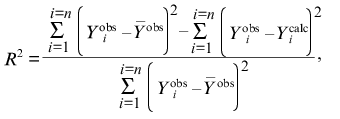 (6)
(6)
where
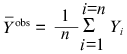 is the average of the experimental data
(Yiobs), Ycalc is the
theoretically calculated value of the function Y, and n
is the number of measurements.
is the average of the experimental data
(Yiobs), Ycalc is the
theoretically calculated value of the function Y, and n
is the number of measurements.
NEW EMPIRICAL EQUATION
Consider the situation when the deviations from Michaelian kinetics are due to interactions between substrate-binding sites in the molecule of oligomeric enzyme. Assume that owing to such interactions the effective Michaelis constant Kmeff is linearly changed with increasing the v/Vmax ratio:
where K0 and Klim are the values of Km at v/Vmax --> 0 and v/Vmax --> 1, respectively. The dependence of v on [S] has the following form:
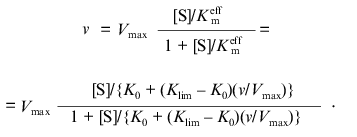 (8)
(8)The equation can be transformed in such a way that its right part contains only the substrate concentration:
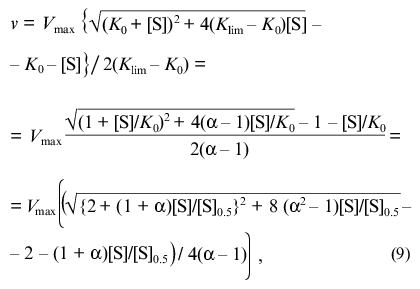
where [S]0.5 is the “semisaturation” concentration: [S]0.5 = (K0 + Klim)/2; alpha refers to the Klim/K0 ratio.
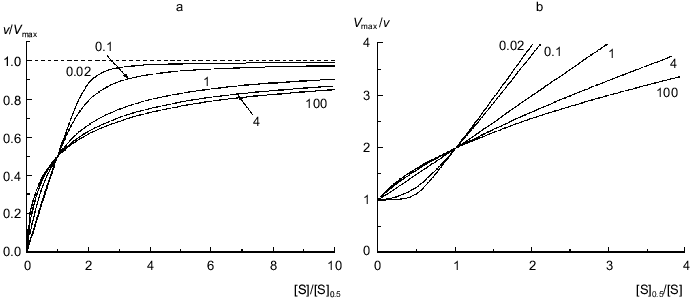
Figure 1a shows the theoretical dependences of the relative enzymatic rate v/Vmax on the dimensionless substrate concentration [S]/[S]0.5 calculated from Eq. (9) at various values of the Klim/K0 ratio (Klim/K0 = alpha). At alpha = 1 the dependence of v/Vmax on [S]/[S]0.5 is evidently hyperbolic. At alpha > 1 the deviations from Michaelian kinetics are manifested in convex curves in reciprocal coordinates (Fig. 1b). Such curves correspond to the situation when the affinity to substrate decreases with the degree of saturation of substrate-binding sites in the enzyme oligomer (negative cooperativity). At alpha < 1 the deviations from Michaelian kinetics are manifested in convex curves in reciprocal coordinates (Fig. 1b). Such curves correspond to the special type of positive cooperative interactions between substrate-binding sites in the enzyme oligomer, when these interactions show themselves not as the S-shaped v versus [S] curves (as usually happens with the allosteric enzymes) ([2], pp. 32-35) but as a sharper approaching the limiting value of the enzymatic reaction rate with increasing the substrate concentration in comparison with the hyperbolic law. Thus, it is of interest to check the applicability of the empirical equation proposed by us for description of two types of deviations from hyperbolic kinetics: negative cooperativity and the case of sharp approaching the limiting value of the enzymatic reaction rate at [S] --> infinity.
If the dependence of v on [S] follows expression (8), the variation of the order of the enzymatic reaction rate with respect to substrate nS = dlogv/dlog[S] with increasing v/Vmax ratio is described by the equation:Fig. 1. Theoretical dependences of the rate of the enzymatic reaction on the substrate concentration calculated from Eq. (9) at various values of the Klim/K0 ratio (Klim/K0 = alpha) in coordinates {v/Vmax; [S]/[S]0.5} (a) and in reciprocal coordinates (b). Numbers near the curves refer to the values of alpha.
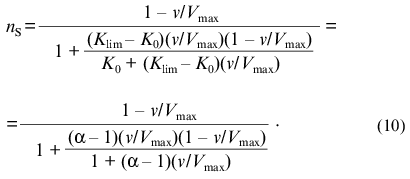
It should be noted that, when describing kinetic anomalies by the Hill equation, negative cooperativity is characterized by values of the Hill coefficient less than unity. When we use empirical equation (8), the degree of deviations from the hyperbolic law is characterized by the Klim/K0 ratio (Klim/K0 = alpha). It is of interest to compare the values of the Hill coefficient with the alpha values for the dependences of v on [S] relating to the case of negative cooperativity. Taking into account that h = dlog[(v/Vmax)/(1 - v/Vmax)]/dlog[S] = nS/(1 - v/Vmax), we can get the following relationship between the value of h at the point of semisaturation (i.e., at v/Vmax = 0.5) and the value of alpha: h0.5 = 2(1 + alpha)/(1 + 3alpha). If alpha = 1, the h0.5 value is equal to 1. As the value of alpha increases, the value of h0.5 decreases (h0.5 --> 2/3 = 0.667 at alpha --> infinity).
It should be noted that if the experimental data allow the limiting value of v at [S] --> infinity to be estimated, the value of Vmax obtained in such a way can be directly used for calculation of the values of the effective Michaelis constant:
The construction of the Kmeff versus v/Vmax plot allows us to prove the assumption that the effective Michaelis constant linearly increases with increasing the v/Vmax ratio.
Equation (8) can be written as a function of v/[S] of v:
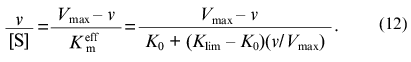
Thus, the experimental data can be analyzed in coordinates {v/[S]; v}. These coordinates are equivalent to the well-known Scatchard coordinates which are applied for analysis of binding of ligands by proteins: {r/[L]; r} (r is concentration of bound ligand divided by the protein concentration and [L] is equilibrium concentration of ligand).
When v --> 0 the curve in coordinates {v/[S]; v} approaches a linear asymptote:
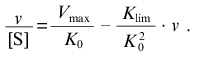 (13)
(13)The intercept on the ordinate axis is Vmax/K0.
The linear asymptote at v --> Vmax has the following form:
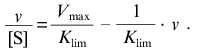 (14)
(14)The intercept on the abscissa axis corresponds to Vmax and the slope of the asymptote is equal to -1/Klim.
When analyzing the deviations of the functions of saturation of protein by ligand from the hyperbolic law, we can use the equations equivalent to Eqs. (8), (9), and (12):
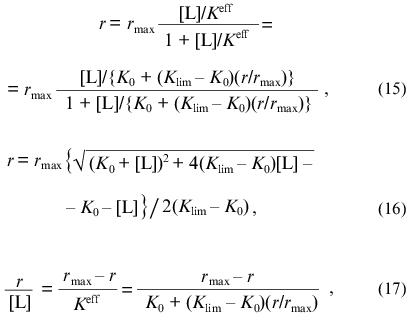
where r is the number of ligand molecules bound by one protein molecule, rmax is the adsorption capacity of the protein (the limiting number of ligand molecules bound by one protein molecule), and [L] is the equilibrium concentration of ligand. In Eqs. (15) and (17) Keff refers to the effective dissociation constant for the complex of protein with ligand, which is a linear function of the r/rmax ratio: Keff = K0 + (Klim - K0)(r/rmax), where K0 and Klim are the limiting values of Keff at r --> 0 and r --> rmax, respectively.
At r --> 0 the curve in coordinates {r/[L]; r} approaches a linear asymptote:
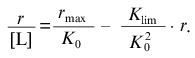 (18)
(18)The intercept on the ordinate axis is equal to rmax/K0.
The linear asymptote at r --> rmax has the following form:
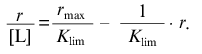 (19)
(19)The intercept on the abscissa axis is equal to rmax and the slope of the asymptote is equal to -1/Klim.
ANALYSIS OF EXPERIMENTAL DATA
Dependences of the Enzymatic Reaction Rate on the Substrate Concentration
We demonstrate the applicability of empirical equation (8) for description of the dependences of v on [S] of abnormal form using glutamate dehydrogenase and biosynthetic threonine deaminase as examples.
Glutamate dehydrogenase. Glutamate dehydrogenases catalyzing transformation of L-glutamate to 2-oxoglutarate or the reverse reaction have a pivotal role in nitrogen and carbon metabolism [6]. Mammalian glutamate dehydrogenase (EC 1.4.1.3) uses NAD and NADP as a coenzyme with comparable efficacy. The enzymatic properties and structure of glutamate dehydrogenase from beef liver mitochondria have been studied in detail. The enzyme molecule consists of six identical subunits with molecular mass of 56 kD each. One of the distinctive kinetic characteristics of beef liver glutamate dehydrogenase is a non-hyperbolic character of the dependence of the enzymatic reaction rate on NAD concentration: the dependence of the reciprocal value of the enzymatic reaction rate on 1/[NAD] is convex [7-11]. Analysis of such dependences using the Hill equation gives Hill coefficient values less than unity. Recently Peterson and Smith [12] have determined the atomic structure of bovine glutamate dehydrogenase in complex with NADH, glutamate, and the allosteric inhibitor GTP to 2.8 Å resolution. The molecule of glutamate dehydrogenase is a dimer of trimers stacked on top of each other with 32 symmetry (one symmetry axis of the third order and three symmetry axes of the second order). Antennae involving a 23-residue helical segment and a 25-residue random coil segment protrude from the body of each subunit. The antennae from each trimer are twisted counterclockwise along the threefold axis. It is suggested that the subunit interactions within the antenna region play an important role in the realization of the mechanism of allosteric regulation [12]. Two sites for NADH binding have been observed in each subunit: one NADH molecule is bound in the active site and the other NADH molecule is bound in the allosteric site, the distance between the active and allosteric sites being ~20 Å.
Banerjee et al. [13] showed that each subunit of beef liver glutamate dehydrogenase contains two NAD-binding sites with equal affinity to NAD. However, in the presence of the product of the enzymatic reaction (2-oxoglutarate) the affinity to one site (presumed to be the active site) is considerably increased.
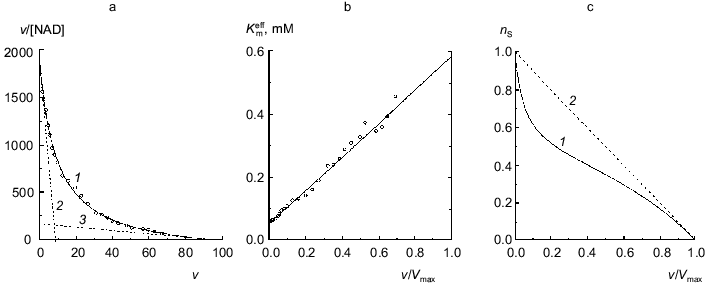
The dependence of the rate of the enzymatic reaction catalyzed by beef liver glutamate dehydrogenase on the concentration of NAD in a wide range of concentrations of coenzyme encompassing three orders of the magnitude was first obtained by Dalziel and Engel [7]. We have analyzed a dependence of such type obtained in more recent work by Engel [10]. Figure 2a shows the dependence of the enzymatic reaction rate on NAD concentration in coordinates {v/[NAD]; v}. The v value refers to the specific enzymatic activity, i.e., the rate of the enzymatic reaction divided by the enzyme concentration. The measurements of the enzymatic activity were carried out in the range of NAD concentrations from 0.001 to 1 mM. Application of Eq. (12) for description of the dependence of v/[NAD] on v gives the following values of parameters: Vmax = 97 ± 7 sec-1, K0 = 0.052 ± 0.004 mM, and Klim = 0.58 ± 0.11 mM (R2 = 0.9970). The Klim/K0 ratio is found to be 11 ± 3. The value of [S]0.5 calculated as (Klim + K0)/2 is equal to 0.32 ± 0.11 mM. Figure 2b demonstrates the linear character of the dependence of the effective Michaelis constant Kmeff calculated from Eq. (11) on the relative rate of the enzymatic reaction v/Vmax.
It is of interest to give the results of analysis of the dependence of the enzymatic reaction rate catalyzed by beef liver glutamate dehydrogenase on NAD concentration under discussion using the Hill equation: Vmax = 105 ± 6 sec-1, [S]0.5 = 0.40 ± 0.07 mM, and h = 0.65 ± 0.02 (R2 = 0.9993).Fig. 2. Analysis of the dependence of the rate of the enzymatic reaction catalyzed by beef liver glutamate dehydrogenase on NAD concentration (Na-phosphate buffer, pH 7.0, I = 0.25, 25°C, 50 mM glutamate) [10]. a) The kinetic data in coordinates {v/[NAD]; v}. The dimension of [NAD] is mM; the dimension of v, specific enzymatic activity, is sec-1. Points are experimental data. Solid curve 1 is calculated from Eq. (12) at values of parameters given in the text. Straight lines 2 and 3 are asymptotes calculated from Eqs. (13) and (14), respectively. b) The dependence of the effective Michaelis constant Kmeff defined by Eq. (11) on the v/Vmax ratio. c) The dependence of the order of the enzymatic reaction rate with respect to substrate nS on the v/Vmax ratio (curve 1 corresponds to the experimental dependence of v on [NAD]; straight line 2 corresponds to the hyperbolic dependence of v on [S]).
The dependence of the order of the enzymatic reaction rate with respect to substrate nS on the v/Vmax ratio represented in Fig. 2c (curve 1) is calculated by Eq. (10). When the dependence of v on [S] follows the hyperbolic law, the nS value linearly decreases with increasing the v/Vmax ratio (straight line 2). The order of the enzymatic reaction rate with respect to substrate characterizes the sensitivity of the enzymatic reaction rate to variation of the substrate concentration. The comparison of curves 1 and 2 directly demonstrates that the enzymatic reaction rate catalyzed by glutamate dehydrogenase is characterized by lower sensitivity to variation of the coenzyme concentration than the rate of the enzymatic reaction following Michaelian kinetics. Therein probably lies the physiological significance of negative cooperativity for glutamate dehydrogenase ([14-16] and also [2], pp. 68-70).
Bacterial glutamate dehydrogenases, for example, dehydrogenase from Clostridium symbiosum, also show non-Michaelian kinetics. The three-dimensional structure of NAD+-linked glutamate dehydrogenase from Clostridium symbiosum has been solved to 1.96 Å resolution [17]. The enzyme molecule is a hexamer with 32 symmetry composed from six identical subunits with molecular mass of 48 kD. Each subunit consists of two domains separated by a deep cleft. NAD is bound in an extended conformation with the nicotinamide moiety deep in the cleft between the two domains.
In order to elucidate the mechanism of negative cooperativity for glutamate dehydrogenase from Clostridium symbiosum, Aghajanian and Engel studied hybridization of the wild-type enzyme and the mutant form of the enzyme in which Cys320 was replaced by serine [18]. Modification of residue Cys320 in the wild-type enzyme by SH-reagents results in full inactivation of the enzyme. By contrast, C320S-mutant, which has catalytic characteristics close to those of the wild-type enzyme, is insensitive to treatment with SH-reagents. Aghajanian and Engel obtained [18] the hybrid form containing five subunits of the wild-type enzyme modified by 5,5´-dithiobis-(2-nitrobenzoate) and one subunit of C320S-mutant. In this hybrid form, only the subunit belonging to C320S-mutant is catalytically active. After treatment of this hybrid form with beta-mercaptoethanol, all six subunits of the hexamer become active.
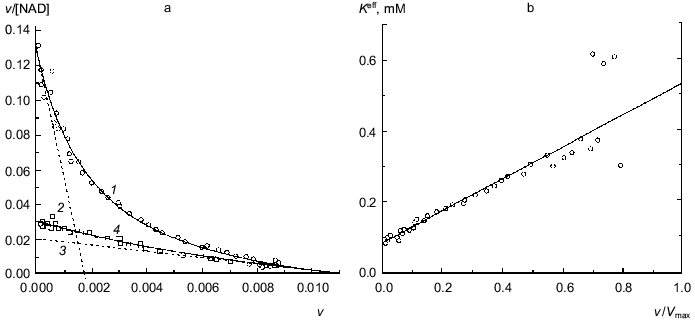
When studying the dependence of the enzymatic reaction rate on NAD concentration for hexamer with six active subunits, clearly defined negative cooperativity is observed: the curves in coordinates {v/[NAD]; v} are concave (Fig. 3a, open circles). The application of Eq. (12) for description of the dependence of v/[NAD] on v gives the following values of parameters: Vmax = 0.0109 ± 0.0010 units, K0 = 0.083 ± 0.007 mM, and Klim = 0.53 ± 0.12 mM (R2 = 0.9839). The Klim/K0 ratio is equal to 6.4 ± 1.9. Figure 3b demonstrates the linear character of the dependence of the effective Michaelis constant Kmeff calculated from Eq. (11) on the relative rate of the enzymatic reaction v/Vmax.
The experimental dependence of v on [NAD] has been analyzed also using the Hill equation: Vmax = 0.0098 ± 0.0003 units, [S]0.5 = 0.21 ± 0.02 mM, and h = 0.80 ± 0.03 (R2 = 0.9955).Fig. 3. Analysis of the dependence of the rate of the enzymatic reaction catalyzed by glutamate dehydrogenase from Clostridium symbiosum on NAD concentration (0.1 M K-phosphate buffer, pH 7.0, 25°C, 40 mM glutamate) [18]. a) The kinetic data in coordinates {v/[NAD]; v}. The dimension of [NAD] is mM. Open circles correspond to hexamer with six active subunits; open squares correspond to hexamer with one active subunit (enzyme concentrations were 2.35 and 0.35 µg/ml, respectively) (4). Solid curve 1 is calculated from Eq. (12) at the values of parameters given in the text. Straight lines 2 and 3 are asymptotes calculated from Eqs. (13) and (14), respectively. b) The dependence of the effective Michaelis constant Kmeff defined by Eq. (11) on the v/Vmax ratio for hexamer with six active subunits.
The catalytic activity of hexamer containing one active subunit of C320S-mutant was measured at an enzyme concentration that was about 6 times lower than the concentration of fully active enzyme form. As seen from Fig. 3a, there is no pronounced negative cooperativity for the enzyme form with one active subunit in hexamer (open squares) and the dependence of v/[NAD] on v is close to the limiting asymptote for hexamer with active subunits corresponding to the region v --> Vmax. Thus, data obtained can be considered as direct evidence that the reason of kinetic anomalies for glutamate dehydrogenase from Clostridium symbiosum is interactions between NAD-binding sites in the hexameric enzyme molecule. It is believed that the formation of hexamer from subunits is accompanied by a marked decrease in the Michaelis constant for NAD (i.e., increase in affinity to NAD) for each subunit. As the hexameric enzyme molecule is saturated by coenzyme, the influence of neighbor subunits is weakened and the Michaelis constant increases to the value corresponding to free subunit.
Biosynthetic threonine deaminase. Biosynthetic threonine deaminase (EC 4.2.1.16) participates in the control of synthesis of the branched-chain amino acids in plants and microorganisms [19-22]. Oligomeric structure and mechanism of allosteric regulation of the enzyme from Escherichia coli have received the most study [23-28]. The molecule of biosynthetic threonine deaminase from E. coli is a tetramer with 222 symmetry consisting of identical subunits with molecular mass of 56 kD.
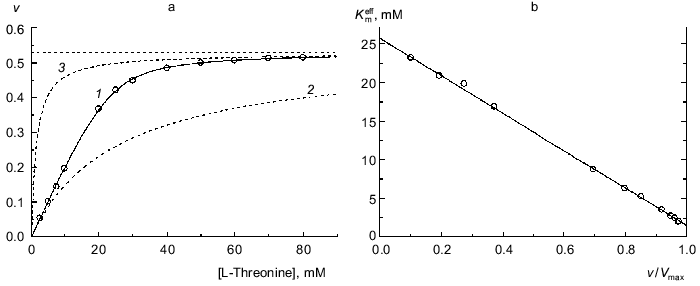
When analyzing the kinetics of the enzymatic reaction catalyzed by biosynthetic threonine deaminase from pea seedlings, we observed kinetic anomalies, which are manifested in “sharper” approaching the limiting value of the enzymatic reaction rate with increasing substrate concentration in comparison with the hyperbolic law [29]. Figure 4a shows the dependence of the enzymatic reaction rate on the substrate concentration (L-threonine) obtained in [29]. For such type of kinetic anomalies the Hill coefficient is close to unity at relatively low values of the v/Vmax ratio; however the Hill coefficient exceeds unity at v/Vmax higher than 0.5 [29]. Equation (9) describes satisfactorily the experimental dependence of v on [S] (Fig. 4a; solid curve). The following values of parameters are obtained: Vmax = 0.529 ± 0.003 µmoles of alpha-ketobutyric acid formed in 1 h per mg of protein, K0 = 25.7 ± 0.5 mM, and Klim = 1.51 ± 0.15 mM (R2 = 0.9998). The Klim/K0 ratio is equal to 0.059 ± 0.007. The dependences of the enzymatic reaction rate on the substrate concentration calculated from the Michaelis equation with the Michaelis constants equal to 25.7 mM (Km = K0) and 1.51 mM (Km = Klim) are presented in Fig. 4a by the dotted lines. Figure 4b demonstrates the linear character of the dependence of the effective Michaelis constant calculated from Eq. (11) on the relative rate of the enzymatic reaction v/Vmax. Thus, the character of the interactions between the substrate-binding sites in biosynthetic threonine deaminase from pea seedlings is that which results in 17-fold decrease in the Michaelis constant as the enzyme oligomer is saturated by the substrate.
Functions of Saturation of Protein by LigandFig. 4. Analysis of the kinetics of the enzymatic reaction catalyzed by threonine deaminase from pea seedlings. a) The dependence of the enzymatic reaction rate v on concentration of L-threonine (0.1 M phosphate buffer, pH 9.1; 30°C) [29]. Points are experimental data. Solid curve 1 is calculated from Eq. (9) at values of parameters given in the text. Curves 2 and 3 are calculated from Eq. (1) at values of Km equal to 25.7 and 1.5 mM, respectively. The horizontal line corresponds to Vmax. The dimension of v is µmoles of alpha-ketobutyric acid formed in 1 h per mg of protein. b) The dependence of the effective Michaelis constant Kmeff defined by expression (11) on the v/Vmax ratio.
We demonstrated the applicability of empirical equation (8) for description of negative cooperativity for functions of saturation of protein by ligand using data on binding of ligands by glutamate dehydrogenase and BSA as examples.
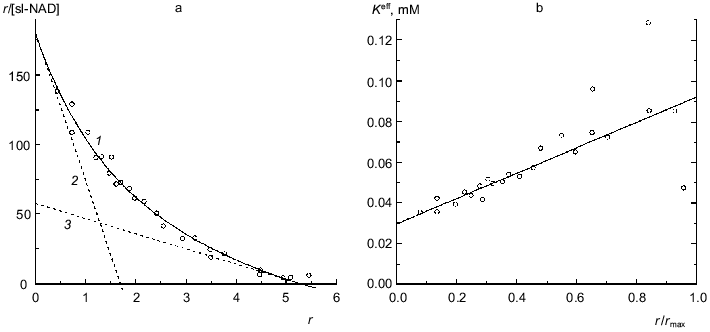
Glutamate dehydrogenase. Figure 5 shows data on binding of a spin-labeled analog of NAD (sl-NAD) by beef liver glutamate dehydrogenase in the presence of 2-oxoglutarate (0.1 M phosphate buffer, pH 7.4, 20°C; [30]). sl-NAD is capable of functioning as a coenzyme in the enzymatic reaction catalyzed by glutamate dehydrogenase. As seen from Fig. 5a, binding of sl-NAD is characterized by negative cooperativity. The experimental data can be satisfactorily described by Eq. (17) at the following values of parameters: rmax = 5.3 ± 0.2, K0 = 0.0295 ± 0.0015 mM, and Klim = 0.0924 ± 0.013 mM (R2 = 0.9841). The Klim/K0 ratio is equal to 3.1 ± 0.6. Asymptotes at r --> 0 and r --> rmax are drawn in Fig. 5a by the dotted lines. Figure 5b shows the linear character of the dependence of the effective dissociation constant Keff for the complex of protein with ligand calculated with the formula
on the r/rmax ratio. Thus, as in the case of NAD [13], in the presence of 2-oxoglutarate only six coenzyme-binding sites in the molecule of glutamate dehydrogenase show sufficiently high affinity to sl-NAD.
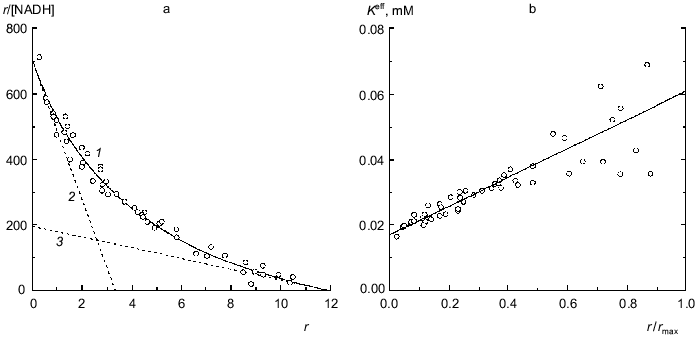
Binding of NADH by beef liver glutamate dehydrogenase is also characterized by negative cooperativity (0.067 M Na-phosphate buffer, pH 7.6; 20°C) [31]. The experimental data represented in Fig. 6a can be satisfactorily described by Eq. (17) at the following values of parameters: rmax = 11.9 ± 0.6, K0 = 0.0169 ± 0.0008 mM, and Klim = 0.061 ± 0.009 mM (R2 = 0.9810). The Klim/K0 ratio is equal to 3.6 ± 0.7. Figure 6b demonstrates the linear character of the dependence of the effective dissociation constant for the complex of protein with ligand calculated with formula (20) on the r/rmax ratio. The value of rmax obtained (rmax ~ 12) means that each subunit of the hexameric molecule of glutamate dehydrogenase contains two NADH-binding sites.Fig. 5. Analysis of data on binding of spin-labeled NAD (sl-NAD) by beef liver glutamate dehydrogenase in the presence of 80 mM 2-oxoglutarate (0.1 M Na-phosphate buffer, pH 7.4) [30]. a) Binding curve in Scatchard coordinates. [sl-NAD] is equilibrium concentration of sl-NAD (mM). Points are experimental data. Solid curve 1 is calculated from Eq. (17) at the values of parameters given in the text. Straight lines 2 and 3 are asymptotes corresponding to Eqs. (18) and (19). b) The dependence of the effective dissociation constant Keff defined by Eq. (20) on the r/rmax ratio.
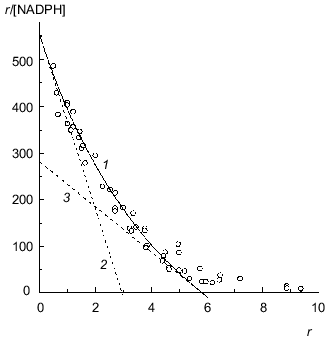
The study of binding of NADPH by beef liver glutamate dehydrogenase showed that only 6 from 12 coenzyme-binding sites have significantly high affinity to NADPH (Fig. 7; [31]). This circumstance allowed us to apply Eq. (17) to the initial part of the isotherm of binding (r <= 4.6). The following values of parameters have been obtained: rmax = 5.8 ± 0.3, K0 = 0.0104 ± 0.0004 mM, and Klim = 0.021 ± 0.004 mM (R2 = 0.9841). The Klim/K0 ratio is equal to 2.0 ± 0.5.Fig. 6. Analysis of the data on binding of NADH by beef liver glutamate dehydrogenase (0.067 M Na-phosphate buffer, pH 7.6; 20°C) [31]. a) Binding curve in Scatchard coordinates. [NADH] is equilibrium concentration of NADH (mM). Points are experimental data obtained by the sedimentation method. Solid curve 1 is calculated from Eq. (17) at the values of parameters given in the text. Straight lines 2 and 3 are asymptotes corresponding to Eqs. (18) and (19). b) The dependence of the effective dissociation constant Keff defined by Eq. (20) on the r/rmax ratio.
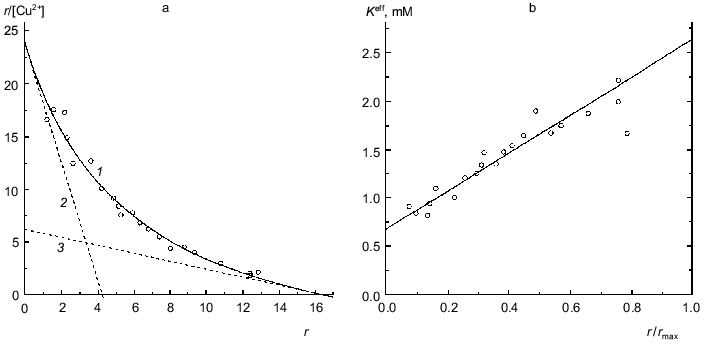
BSA. Figure 8a is a Scatchard plot for data on binding of Cu2+ by BSA obtained by Klotz and Curne [32]. It should be noted that these experimental data were the subject of the theoretical analysis in [33, 34]. The dependence of r/[Cu2+] on r is concave. The reason is evidently that Cu2+-binding sites are non-equivalent. As can be seen from Fig. 8a, the experimental data are described satisfactorily by Eq. (17). The values of parameters are the following: rmax = 16.4 ± 1.6, K0 = 0.68 ± 0.06 mM, Klim = 2.6 ± 0.8 mM (R2 = 0.9745). The Klim/K0 ratio is equal to 3.9 ± 1.4.Fig. 7. Analysis of data on binding of NADPH by beef liver glutamate dehydrogenase in Scatchard coordinates (0.067 M Na-phosphate buffer, pH 7.6; 20°C) [31]. [NADPH] is the equilibrium concentration of NADPH (mM). Points are experimental data obtained by the sedimentation method. Solid curves 1 are calculated from Eq. (17) at the values of parameters given in the text. Straight lines 2 and 3 are asymptotes corresponding to Eqs. (18) and (19).
Figure 8b demonstrates the linear character of the effective dissociation constant Keff for the complex of protein with ligand calculated from Eq. (20) on the r/rmax ratio.
Fig. 8. Analysis of data on binding of Cu2+ by BSA (Na-acetate buffer, pH 4.83, 25°C) [32]. a) Scatchard plot. [Cu2+] is the equilibrium concentration of Cu2+ (mM). Points are the experimental data. Solid curve 1 calculated from Eq. (17) at the values of parameters given in the text. The straight lines 2 and 3 are asymptotes corresponding to Eqs. (18) and (19). b) The dependence of the effective dissociation constant Keff defined by expression (20) on the r/rmax ratio.
PHYSICAL MEANING OF PARAMETERS K0 AND Klim
Consider the situation when deviations of the functions of protein saturation by ligand from the hyperbolic law are connected with interactions between ligand-binding sites in the protein oligomer resulting in a change in the affinity to ligand as ligand-binding sites in the protein molecule are occupied by ligand. In this case parameters K0 and Klim are the limiting values of the dissociation constant corresponding to initial (r/rmax --> 0) and final (r/rmax --> 1) steps of saturation of protein by ligand.
It is of special interest to discuss what kinds of interactions between ligand-binding sites in the protein molecule can result in the linear dependence of the effective dissociation constant on the r/rmax ratio. Assume that the protein molecule contains n equivalent ligand-binding sites interacting with each other. Let Ki be the microscopic dissociation constant for the protein-ligand complex containing i molecules of ligand (P is the protein molecule):
The function of saturation of protein by ligand has the following form ([2], p. 122):
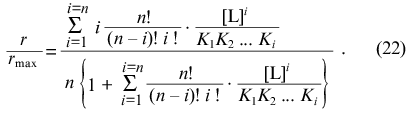
Negative interactions between ligand-binding sites corresponds to the case when the values of Ki increase with increasing i, whereas positive interactions between ligand-binding sites corresponds to the case when the values of Ki decrease with increasing i.
Consider, for example, the situation when the molecule of a model protein contains six equivalent ligand-binding sites interacting with each other. Assume that the saturation function is described by empirical equation (15) and the Klim/K0 ratio is equal to 10 (alpha = 10). Let K0 = K1 be 1 mM (Klim = K6 = 10 mM). We have constructed the theoretical dependence of r on [L] in the range of values of [L] from 10-2 to 103 mM and selected 100 points uniformly distributed on the logarithmic scale in this interval. The model curve was described further by Eq. (22). The following values of Ki were obtained:
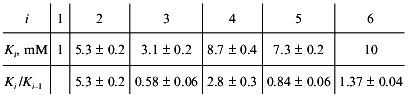
Analysis of the experimental data on glutamate dehydrogenase allows us to suggest that non-hyperbolic character of the dependence of the enzymatic reaction rate on NAD concentration is due to interactions between six NAD-binding sites in a hexameric enzyme molecule. If we assume further that interactions between the active sites result only in the change in the Michaelis constant (but not the catalytic constant), the calculated values of K0 and Klim give the estimations of Km for NAD at v/Vmax --> 0 and v/Vmax --> 1, respectively.
Consider the situation when alpha < 1. Let alpha = 0.1. We assume that the molecule of a model protein contains four identical and non-interacting sites. Let K0 = K1 = 1 mM (Klim = K4 = 0.1 mM). We constructed the theoretical dependence of r on [L] in the range of the values of [L] from 3·10-3 to 3·10 mM and selected 100 points in this range. Thereupon the model curve was described by Eq. (22). The following values of Ki were obtained:
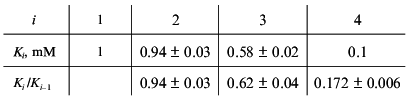
What is the physical meaning of parameters Klim and K0 for the case when ligand-binding sites in the protein molecule are non-identical? The saturation function for the protein containing n non-identical and non-interacting ligand-binding sites has the following form:
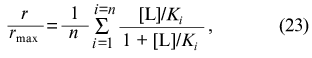
where Ki is the microscopic dissociation constant for binding of ligand in the site of type i. At r --> 0 we get the following expression for r/rmax:
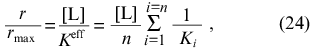
and, consequently,
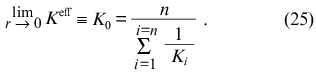
At r --> rmax the expression
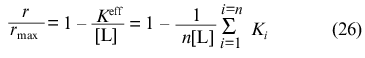
holds for r/rmax and, consequently,
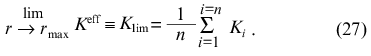
Thus, the calculation of rmax, K0, and Klim allows the following combinations of constants Ki to be obtained: the sum of reciprocal values of Ki and the sum of values of Ki (note that rmax = n).
Consider, for example, the situation when the molecule of a model protein contains six non-identical and non-interacting ligand-binding sites. Assume that the saturation function is described by empirical equation (15) and the Klim/K0 ratio is equal to 10 (alpha = 10). Let K0 be 1 mM (Klim = 10 mM). We described the model dependence of r on [L] by Eq. (23) in the range of values of [L] from 10-2 to 103 mM. The following values of Ki given in order in their increasing were obtained:
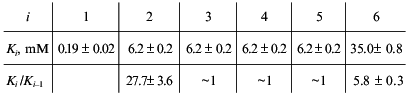
It seems likely that negative cooperativity observed for binding of NADH by beef liver glutamate dehydrogenase (Fig. 6) is due to non-equivalency of NADH-binding sites as well as to interactions between NADH-binding sites in the enzyme molecule. As for binding of NADPH, negative cooperativity for this ligand (for the initial part of the isotherm of binding) is due solely to interactions between NADPH-binding sites in the glutamate dehydrogenase molecule.
The empirical equation proposed can be used for the quantitative description of the deviations from Michaelian kinetics, which manifest themselves as “negative cooperativity” (convex curves in coordinates {1/v; 1/[S]} or concave curves in coordinates {v/[S]; v}, as well as for description of negative cooperativity for the functions of saturation of protein by ligand. The equation contains three parameters: Vmax (or rmax), K0, and Klim. The Klim/K0 ratio can be considered as a characteristic of the degree of deviations of the experimental curve from the hyperbolic law. If the protein molecule contains (1) n equivalent ligand-binding sites interacting with each other or (2) n non-identical and non-interacting ligand-binding sites, parameters K0 and Klim have clear physical meaning. In the former case K0 = K1 and Klim = Kn (K1 and Kn are the microscopic dissociation constants for complexes of protein with ligand containing one and n ligand molecules, respectively). The relationship between parameters K0 and Klim allows the free energy of intersubunit interaction to be estimated [35]: DeltaF = -RTln(K1/Kn) = -RTln(K0/Klim). In the latter case parameters K0 and Klim are defined by Eqs. (25) and (27), and the Klim/K0 ratio is equal to:
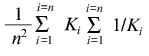
(Ki is the microscopic dissociation constant for binding of ligand in the site of type i).
This study was funded by grants 99-04-48639 and 00-15-97787 from the Russian Foundation for Basic Research.
REFERENCES
1.Hill, C. M., Waight, R., and Bardsley, W. G. (1977)
Mol. Cell. Biochem., 15, 173-178.
2.Kurganov, B. I. (1982) Allosteric Enzymes.
Kinetic Behaviour, J. Wiley and Sons, Chichester.
3.Ainsworth, S. (1977) J. Theor. Biol.,
68, 391-413.
4.Ainsworth, S., and Gregory, R. B. (1978) J.
Theor. Biol., 75, 97-114.
5. Scientist for Experimental Data Fitting.
Microsoft Windows Version 2.0 (1995) MicroMath, Inc., Salt Lake
City, p. 466.
6.Hudson, R. C., and Daniel, R. M. (1993) Comp.
Biochem. Physiol. B, 106, 767-792.
7.Dalziel, K., and Engel, P. C. (1969) FEBS
Lett., 1, 349-352.
8.Engel, P. C., and Dalziel, K. (1969) Biochem.
J., 115, 621-631.
9.Markau, K., Schneider, J., and Sund, H. (1972)
FEBS Lett., 24, 32-36.
10.Engel, P. C., and Ferdinand, W. (1973)
Biochem. J., 131, 97-105.
11.Electricwala, A. H., and Dickinson, F. M. (1979)
Biochem. J., 177, 449-459.
12.Peterson, P. E., and Smith, T. J. (1999)
Structure, 7, 769-782.
13.Banerjee, A., Levy, H. R., Levy, G. C., LiMuti,
C., Goldstein, B. M., and Bell, J. E. (1987) Biochemistry,
26, 8443-8450.
14.Cornish-Bowden, A. (1975) J. Theor. Biol.,
51, 233-235.
15.Levitzki, A. (1978) Quantitative Aspects of
Allosteric Mechanisms, Springer-Verlag, Berlin, pp. 79-88.
16.Ghosh, R. (1981) J. Theor. Biol.,
93, 395-401.
17.Baker, P. J., Britton, K. L., Engel, P. C.,
Farrants, G. W., Lilley, K. S., Rice, D. W., and Stillman, T. J. (1992)
Proteins: Struct. Funct. Genet., 12, 75-86.
18.Aghajanian, S., and Engel, P. C. (1998)
Protein Eng., 11, 569-575.
19.Szentirmai, A., and Horvath, I. (1976) Acta
Microbiol. Acad. Sci. Hung., 23, 137-149.
20.Iaccarino, M., Guardiola, J., De Felice, M., and
Favre, R. (1978) Curr. Top. Cell. Regul., 14, 29-73.
21.Eikmanns, B. J., Eggeling, L., and Sahm, H.
(1993-1994) Antonie Van Leeuwenhoek, 64, 145-163.
22.Epelbaum, S., LaRossa, R. A., VanDyk, T. K.,
Elkayam, T., Chipman, D. M., and Barak, Z. (1998) J. Bacteriol.,
180, 4056-4067.
23.Kagan, Z. S., Dorozhko, A. I., Kovaleva, S. V.,
and Yakovleva, L. I. (1975) Biochim. Biophys. Acta, 403,
208-220.
24.Eisenstein, E. (1991) J. Biol. Chem.,
266, 5801-5807.
25.Eisenstein, E., Yu, H. D., and Schwarz, F. P.
(1994) J. Biol. Chem., 269, 29423-29429.
26.Eisenstein, E. (1995) Arch. Biochem.
Biophys., 316, 311-318.
27.Chinchilla, D., Schwarz, F. P., and Eisenstein,
E. (1998) J. Biol. Chem., 273, 23219-23224.
28.Gallagher, D. T., Gilliland, G. L., Xiao, G.,
Zondlo, J., Fisher, K. E., Chinchilla, D., and Eisenstein, E. (1998)
Structure, 6, 465-475.
29.Kagan, Z. S., Khashimov, D. A., and Kurganov, B.
I. (1970) Biokhimiya, 35, 937-952.
30.Zantema, A., Trommer, W. E., Wenzel, H., and
Robillard, G. T. (1977) Eur. J. Biochem., 72,
175-184.
31.Krause, J., Büchner, M., and Sund, H. (1974)
Eur. J. Biochem., 41, 593-602.
32.Klotz, I. M., and Curme, H. G. (1948) J. Amer.
Chem. Soc., 70, 939-943.
33.Klotz, I. M., and Hunston, D. L. (1975) J.
Biol. Chem., 250, 3001-3009.
34.Fletcher, J. E. (1977) J. Phys. Chem.,
81, 2374-2378.
35.Wyman, J. (1964) Adv. Prot. Chem.,
19, 223-286.