REVIEW: Mitochondrial ATP Synthase: Fifteen Years Later

A. D. Vinogradov

Department of Biochemistry, School of Biology, Lomonosov Moscow State University, Moscow, 119899 Russia; fax: (7-095) 939-3955; E-mail: adv@biochem.bio.msu.su

Received June 21, 1999

---

Mitochondrial F_o·F₁-H⁺-ATP synthase is the main enzyme responsible for the formation of ATP in aerobic cells. An alternating binding change mechanism is now generally accepted for the operation of the enzyme. This mechanism apparently leaves no room for the participation of nucleotides and P_i other than sequential binding to (release from) the catalytic sites. However, the kinetics of ATP hydrolysis by mitochondrial ATPase is very complex, and it is difficult to explain it in terms of the alternating binding change mechanism only. F_o·F₁ catalyzes both Deltaµ_H+-dependent ATP synthesis and ATP-dependent Deltaµ_H+ generation. It is generally believed that this enzyme operates as the smallest molecular electromechanochemical reversible machine. This essay summarizes data which contradict this simple reversible mechanism and discusses a hypothesis in which different pathways are followed for ATP hydrolysis and ATP synthesis. A model for a reversible switch mechanism between ATP hydrolase and ATP synthase states of F_o·F₁ is proposed.

---

KEY WORDS: F_o·F₁-ATPase, ATP synthase, reversibility of enzyme catalysis, mitochondria

Gibbsian statistical mechanics may well be a fairly adequate model of what happens in the body; the picture suggested by the ordinary heat engine certainly is not. The thermal efficiency of muscle action means next to nothing, and certainly does not mean what it appears to mean.

Norbert Weiner ("Cybernetics", The M.I.T. press and John Wiley and Sons, Inc., New York, London, 1961, p. 57)

1. INTRODUCTION

Fifteen years ago in the short review article "Catalytic Properties of the Mitochondrial ATP Synthase" published in Biokhimiya (now Biochemistry (Moscow)) [1] I summarized experimental results obtained in the laboratory and raised doubts about a central dogma of enzymology: any enzyme is a catalyst and, because of that, the molecular mechanisms of the forward and reverse enzymatic reactions are identical; the only difference in mechanism is the direction of the transformation of the intermediates (microreversibility principle). It would not be judicious to say that the hypothesis of different reaction mechanisms for ATP hydrolysis and synthesis catalyzed by the mitochondrial F_o·F₁ complex, as it was originally formulated in 1980 [2], has been agreeably accepted by the workers in the field. Most investigators simply ignored our arguments; others argued (explicitly or implicitly) that we attribute a role of a Maxwell's demon to the enzyme, thus violating the Second Law of thermodynamics.

The proton-translocating ATPases have been perhaps the most extensively studied enzymes in bioenergetics during the last decade. The outstanding achievements in the study of structure and mechanism reached by P. Boyer and J. Walker were awarded the 1997 Nobel Prize in Chemistry. In this essay I will summarize some generally accepted concepts on the reaction mechanism of the enzyme and analyze again the problem of its reversibility. The discussion will be mostly focused on the experimental results obtained by my own group, and so this essay is hardly a regular review. A number of comprehensive reviews on the subject have been published during the last decade; each of them contains hundreds references to original papers relevant to the F₁-ATPases studies. It is not unusual that a newcomer in the field will find some contradictory statements in different reviews; this is especially true when the kinetic properties of the enzyme (the particular area where our group has some experience) are discussed. This is why the kinetics of the enzyme is the main subject to be analyzed here.

The mitochondrial H⁺-ATP-synthase (F_o·F₁-H⁺-ATPase) is an extremely complex membrane-bound energy transducing enzyme which produces most of the ATP present in aerobic cells. The substrates--nucleotides and, possibly, inorganic phosphate--bind to (release from) so-called "catalytic sites" located in the hydrophilic part (F₁); F_o, which is an intrinsic part of the inner mitochondrial membrane, serves as the specific proton-conducting path. It is generally accepted that the enzyme operates as follows: the work done by the proton flow down the electrochemical potential gradient (Deltaµ_H+) is transformed to the chemical work needed to synthesize ATP by F₁ according to Eq. (1):

where n is a quotient for stoichiometric vectorial proton translocation from cytoplasm (H⁺_out) to the matrix space (H⁺_in) and m is a stoichiometric quotient for scalar proton consumption which is determined by the difference in total acidity of the substrates (ADP and inorganic phosphate) and product (ATP). The exact value of n (2-4) is not established; m is close to 1 at pH > 7.5 and depends predominantly on pH and Mg²⁺ concentration, which forms more (ATP) or less (ADP and P_i) stable complexes with the reaction product and substrates. Energy-dependent ATP synthesis is phenomenologically reversible: ATP hydrolysis in tightly coupled membranous preparations results a difference between the electrochemical potentials of hydrogen ions (Deltaµ_H+) at different sides of the coupling inner mitochondrial membrane. Whether the ATPase activity of those preparations is a simple reversal of ATP synthesis is not known, since the precise mechanisms of neither ATP hydrolysis nor its synthesis are known.

Spectacular achievements have been made in recent years in elucidating the ternary structure of F₁ at the atomic resolution of 2.8 Å [3, 4]. The F₁ (alpha₃·beta₃·gamma·delta·epsilon subunit composition) appears as a trimer of tightly packed alpha·beta-subunit pairs, and the long, rod-like gamma-subunit, is positioned in the central cavity of the overall spherical, orange-like globular protein [3]. The ternary structure of smaller delta- and epsilon-subunits and their positions relative to the alpha₃·beta₃·gamma heptamer have not been revealed by crystallography. F_o has the structure a·b₂·c_9-12 (the minimal composition); only the structure of the c-subunit, which seems to be a key component of the proton-conducting path, is well established [5]. The catalytic sites residing on F₁ are located far from the plane of the coupling membrane. This spatial separation suggests that Deltaµ_H+-dependent ATP synthesis must be a complex electromechanochemical process. The rotational alternating binding change mechanism originally based on quantitative measurements of isotope exchange reactions [6] and supported by numerous studies including elegant demonstrations of strong negative cooperativity in ATP binding and positive cooperativity in ATP hydrolysis [7, 8] is now widely accepted [9, 10]. Essential features of this mechanism are as follows: 1) the free energy produced by H⁺ flow is used not to synthesize ATP (DeltaG ~ 8 kcal/mole) but to release tightly bound ATP spontaneously (isoenergetically) formed at the very high-affinity ATP-binding site of the enzyme [Footnote: This certainly does not mean that solubilized ATPase is capable of the overall ATP synthesis. Isoenergetic ATP formation at the active site is only "half" of the enzyme turnover. According to the proposed mechanism the driving force for isoenergetic synthesis, at least partially, is a difference between the free energies of binding ATP and ADP + P_i, i.e., chemical work is done by the energy released when the protein conformation is changed from the state when it contains ADP + P_i to the state when it contains ATP. Thus, the isoenergetic ATP synthesis means only that the equilibrium constant for the reversible reaction ADP·E·P_i {} E·ATP is close to 1.]; 2) each catalytic site sequentially (on the turnover time scale) appears as: empty --> tight --> loose in terms of occupation and tightness of nucleotide binding; 3) the occupation and mode of nucleotide binding at one catalytic site within the alpha·beta trimer strictly determine the properties of two other sites.

The most plausible way to realize such a mechanism is to rotate one element of the F₁ structure relative to the trimerically arranged catalytic sites [9]. The spatial structure of F₁ seems to fit ideally the proposed mechanism. Perhaps the most impressive achievements of bioenergetic enzymology recent decades were the original prediction and further indirect demonstration [11-13] and finally direct visualization [14, 15] of ATP-dependent rotation of the gamma-subunit (the rotor) within three alpha·beta-subunit pairs structure (the stator). These exciting results led to the conclusion that F_o·F₁-ATP synthase is the smallest electrical machine created by Nature and a number of technical terms previously unknown to enzymology such as: rotor, shaft, stator, torque, clutch are now widely used to describe the enzyme operation.

The rotational alternating binding change mechanism apparently leaves no alternative for ADP, P_i, ATP, and Deltaµ_H+ but to participate in the overall reaction in a way different from that required for the substrate (product) binding (release) and driving force, respectively, as depicted in Eq. (1). Indeed, the steady-state rates of ATP hydrolysis or synthesis are expected to be strictly determined by occupation of the catalytic sites by nucleotides and P_i only. However, the kinetic properties of either soluble F₁ or membrane-bound F_o·F₁ are far from being trivial.

F_o·F₁-ATPase is now frequently described as a molecular machine and the problem of its reversibility seems to be of great importance. If, according to several language dictionaries, a general definition of a machine is an "assemblage of parts that transit forces, motions and energy from one to another in a predetermined manner" [16] is to be accepted, the question arises: do reversible machines exist? In my opinion the molecular machines created by Nature as well as those created by mankind are made exclusively for unidirectional energy transduction. Thus, a special mechanism(s) that can be switched on or off by the applied driving force, thus permitting unidirectional energy transmission, must be a component of any machine. If ATP synthase is a small electromechanical engine, its performance should be described as a mechanical device and not as thermal engine. An analysis of any mechanical machine in terms of thermodynamics seems to be extremely complex (if not basically unsolvable) problem. Impossibility of the Maxwell demon of the molecular size realized as the well known mechanical ratchet mechanism was brilliantly discussed in detail by R. Feynman [17]. The key point in his arguments is that in the long run the molecular "demon" is itself in a thermal equilibrium with a surrounding media. However, temperature is not a parameter needed to describe a mechanical engine, and a number of ratchet mechanisms (which are certainly not within the molecular size range) smoothly operate in many real devices such as the mechanical clock or windlass. I believe that thermodynamic arguments against unidirectional enzymes are due to some misunderstanding. It is true that any enzyme being a catalyst is not able to change the equilibrium between the substrate and product reached in a reversible reaction. However, this is true only when the enzyme as a mechanical device is not subjected to the energy supply. A possible mechanism which allows an enzyme to operate unidirectionally will be proposed below. Another pertinent question directly related to the present discussion can be formulated as follows: are parts of a molecular machine (enzyme) in thermal equilibrium with the surrounding medium? If so, neither part of this "machine" would be able to operate as an energy transducer; it would dissipate energy (for example that of the conformational constraint) as heat, and the device would not be a "machine". This difficulty can be overcome with the restriction: time needed for thermal relaxation is much longer than that needed for "useful transport" of energy. In this case thermodynamic arguments against the unidirectional enzyme became irrelevant simply because time is not a variable for the thermodynamic functions which determine an equilibrium. The lack of strong theory for an adequate analysis of the systems composed of some parts which are yet neither mechanical devices (cogwheel, crankshaft, etc.) nor the statistical ensemble of small particles, does not permit clear description of miniature machines--the most conceivably perfect devices created by Nature. The natural molecular machines fall just in that in-between range.

2. GENERAL REMARKS ON THE KINETICS OF MITOCHONDRIAL ATPase

When soluble F₁, oligomycin-sensitive purified F_o·F₁, or submitochondrial particles are added to a reaction mixture containing ATP and Mg²⁺, rapid hydrolysis of ATP is observed. The enzyme activity under "optimal" conditions corresponds to a turnover number of several hundreds per second. It might be expected that the standard kinetic parameters of this remarkably stable and highly active enzyme could easily be determined. However this is not the case. Meaningful interpretation of the enzyme kinetics is only possible when the initial steady-state rates are measured. When the hydrolytic activity of F₁-type ATPase is considered, the initial rate, as such, is not an unambiguous term. There are several reasons for this. First, many preparations contain a small natural inhibitory peptide, an ATPase inhibitor protein (IF₁) [18], which is an intrinsic part of the mitochondrial F_o·F₁-ATP synthase. The inhibitory effect of this protein is time-, pH-, ionic-strength-, and ATP-dependent and may also be dependent on Deltaµ_H+ and the presence of divalent cations [18-22]. It appears that uncontrolled contaminations of the protein inhibitor might cause serious errors in measurements of the actual initial velocities of ATPase in many early studies, including our own [23].

Second, the product of ATP hydrolysis, ADP, is an inhibitor of all ATPase preparations. One type of inhibition (rapidly equilibrating competitive) [24] can be easily prevented if ATP-regenerating systems, such as phosphoenolpyruvate and pyruvate kinase or phosphocreatine and creatine kinase, are used in the assays. However, the system becomes more complex when the ATP-regenerating enzymes are present, and the experimental approaches are somehow restricted when nucleotide specificity or metal requirement are being verified because the "regenerating" enzymes themselves depend on the nucleotides and cations (Mg²⁺, K⁺, Ca²⁺) in a complex way. Another unusual type of inhibition (modulation) by ADP which is quite different from "simple equilibrium" and which is characteristic for all F₁-type ATPases [25, 26] and V-type ATPase [27] is a potential source of serious errors in the ATPase assays even in the presence of ATP-regenerating systems. For F₁-type ATPases this ADP-dependent inhibition results in strong dependence of the measured activity on the "history" of a particular preparation. If the enzyme is not subjected to special treatment (see below) the ATP hydrolytic activity is never constant and either "lag" or "burst" are seen even in the presence of ATP-regenerating system added in "kinetic excess". The complexities and possible errors in measurements of the initial rates can hardly be overestimated. Depending on particular assay and the actual time scale, the ADP-dependent inhibition can be easily overseen. For example, if the "initial rates" are measured on a time scale of minutes, the activity is proportional to a fraction of the active enzyme which is in a slow equilibrium with completely inactive form; this equilibrium depends on ATP, Mg²⁺, and anions which are present. On the other hand, if the time intervals are small, the apparent initial rate is again proportional to an unknown fraction of the active enzyme. Although the details of the unusual "hysteretic" behavior of ATPase has been described by us about 20 years ago [28, 29] and more recently were specially emphasized by P. Boyer [9], only a few research groups have paid attention to this phenomenon, and thus the results of ATPase kinetics studies should be interpreted with great caution.

3. STEADY-STATE ATP HYDROLYSIS

Some standard kinetic parameters of ATP hydrolysis by mitochondrial ATPase are summarized in the table and briefly discussed below.

Steady-state kinetic parameters for mitochondrial F_o·F₁-ATPase (submitochondrial particles)^*

^*The quantitative data (right column) are given for pH 7.5, 25°C, ionic strength of 0.1 M (KCl) and refer to the initial rates (10-30 sec) of ATP hydrolysis by completely activated (preincubation with either 10 mM potassium phosphate or phosphoenolpyruvate and pyruvate kinase) F_o·F₁-ATPase.

ATP. ATP and other nucleotides (ITP, GTP) are hydrolyzed at significant rates only in the presence of Mg²⁺ or some other divalent cations (Mn²⁺, Co²⁺, Fe²⁺) [30]. At high Mg²⁺ concentrations (2-10 mM at pH 7.0-8.0) the dependence of the hydrolytic rate on ATP concentration is a simple hyperbolic function within the 2-5000 µM range with an apparent K_m of approximately 10^-4 M [28]. This contrasts with several reports in the literature in which two or three K_m values for ATP have been found [31-33]. There are strong reasons to believe that the non-hyperbolic dependence of ATPase on ATP concentration is due to an erroneous perception of the observed rates as the initial ones (see above). It is worth noting that the experimentally well-documented strong negative cooperativity in ATP binding and extremely positive cooperativity in hydrolytic performance [7, 8] do not conflict with the simple Michaelis--Menten kinetics of the steady-state ATP hydrolysis. So-called uni-site catalysis is seen only under the conditions when the enzyme concentration is several times larger than that of ATP. The affinity for ATP binding to the "first" catalytic site is extremely high (approximately 10^-12 M) and this concentration range is never covered in the standard steady-state kinetic measurements ([S] >> [E]_t). Also, simple Michaelis--Menten kinetics do not conflict with the alternating binding change mechanism [6, 9]: if cooperativity of binding is very strong or absolute (as in the "flip-flop" mechanism [34-36]), a single "entrance" for the substrate and a single "exit" for the products would exist.

An interesting possibility we would like to propose is that, during the steady-state performance of F₁-type ATPase/synthase, a "gate" and special "path" operate which determine the penetration of ATP (or ADP) from the medium into a "catalytic cavity" where three exchangeable sites (out of six total) are located. In the light of the structural arrangement of F₁ [3, 4], it seems unlikely that what are assigned as "catalytic" and "noncatalytic" sites on the beta- and alpha-subunits are readily accessible to nucleotides from the solution. If this proposal is correct, the apparent K_m for ATP is a quantitative measure of the nucleotide affinity to a "gate" and not to the catalytic site(s) where chemical reaction takes place; the latter would contain "occluded" nucleotides.

The K_m value for ATP depends strongly on Mg²⁺ concentration. At high concentration (a significant molar excess over [Mg²⁺]) ATP inhibits ATPase activity [37]. This inhibition is most likely due to a decrease in free [Mg²⁺], which is needed (in addition to that bound as an ATP·Mg complex) for the catalysis (see below).

ADP. ADP, the product of the ATPase reaction, is an inhibitor of the hydrolytic activity. Quantitative and qualitative parameters for inhibition by ADP in terms of the steady-state kinetics are difficult to determine because ADP slowly deactivates the enzyme (the term "deactivation" will be used throughout this article to discriminate a decrease or complete inhibition of only the initial velocity, i.e., the lag phase in the enzyme performance, from the usual inhibition of the activity, see below). From the initial rate measurements it has been concluded that ADP is a simple competitive inhibitor (with ATP) of the hydrolysis [24]. We found that free ADP, not the ADP·Mg complex, competes with the ATP·Mg complex for the "substrate-binding" site [37]. This finding is of particular interest because the ADP·Mg complex was shown to be a true substrate for oxidative phosphorylation catalyzed by submitochondrial particles [38] and for photophosphorylation in chloroplasts [39]. Certainly, as it was pointed out above, one needs to define clearly what is assumed to be the "substrate-binding site": one of those which are seen in the resolved F₁ structure, or it is an apparent affinity to the entrance in the proposed "gate-specific path" mechanism which may contribute significantly in the overall steady-state reaction.

P_i. Although P_i is equally important as ADP as a substrate/product of ATP synthase, only a few studies, compared with those on nucleotide binding, are available on its specific effects on the ATP hydrolysis catalyzed by F₁ or by F_o·F₁. Soluble F₁ has been shown to bind P_i with a relatively high affinity [40, 41]. It would seem logical to expect that P_i must inhibit ATP hydrolysis with an apparent K_i similar to its K_m value for oxidative phosphorylation (in the millimolar range [38]). However, this is not the case, and P_i either has no effect on ATP hydrolysis or it slightly stimulates ATPase activity, as do several other anions. It is extremely difficult, if not impossible, to construct a kinetic scheme which includes the reversible P_i release step and which does not contain a P_i inhibition term in an equation for the steady-state reaction rate. This problem has been somehow overlooked in many detailed discussions of the enzyme mechanism. The only possible explanation for the absence of its inhibitory effect is that P_i irreversibly dissociates from the active site during ATP hydrolysis: this proposal immediately creates an unavoidable problem in viewing ATP synthase as a reversible ATPase.

Mg²⁺. It is well established that Mg²⁺ (or some other divalent cation) is needed for ATPase activity [23, 30, 42]. Since the early publications on ATPase kinetics [23, 42], statements on the inhibition of ATPase by free excess Mg²⁺ have been widely circulated in the literature. Recently, we have reinvestigated the problem and found no inhibition of the enzyme activity by Mg²⁺ (up to 10-15 mM) provided that true initial rates are measured. It appears that the previously reported inhibitory effects of Mg²⁺ were due to underestimations of its other effect: Mg²⁺-induced, ADP-dependent (or vice versa) slow deactivation of the enzyme. Moreover, we found that free Mg²⁺, in addition to that bound in the true substrate (ATP·Mg)^2-, is needed for ATPase activity [37]. The kinetic analysis suggests that activating Mg²⁺ is involved in the overall reaction according to the so-called "ping-pong" mechanism, i.e., it participates after irreversible dissociation of one of the products from the active site. Since the structure of alpha₃·beta₃·gamma at 2.8 Å resolution is now available [3, 4], an obvious question arises: where the Mg²⁺-specific "activating" site is located? The structures of the nucleotide-binding sites in asymmetric F₁ containing Mg²⁺--nucleotide complexes bound to the alpha and beta subunits were visualized. Surprisingly, no Mg²⁺ other than that originating from the Mg²⁺--nucleotide complexes was seen, despite the presence of adenosine-5´-phosphoimidophosphate, ADP, Mg²⁺, and sodium azide and the absence of P_i in the crystallization medium [43]. It is possible that the Mg²⁺-specific site is located on the disordered "invisible" part of the gamma-subunit.

When only a limiting concentration of free Mg²⁺ is available, ATPase activity becomes strongly pH-dependent, as to be expected if Mg²⁺ binds to a deprotonated group with a pK_a of 7.4 [37].

Deltaµ_H+. The ATPase activity of intact mitochondria is greatly stimulated by uncoupling agents. Unfortunately, ATPase of coupled submitochondrial particles is only slightly (not more than twofold) accelerated when Deltaµ_H+ is collapsed. It should be admitted that our knowledge on the possible effects of Deltaµ_H+ on steady-state ATP hydrolysis are very limited.

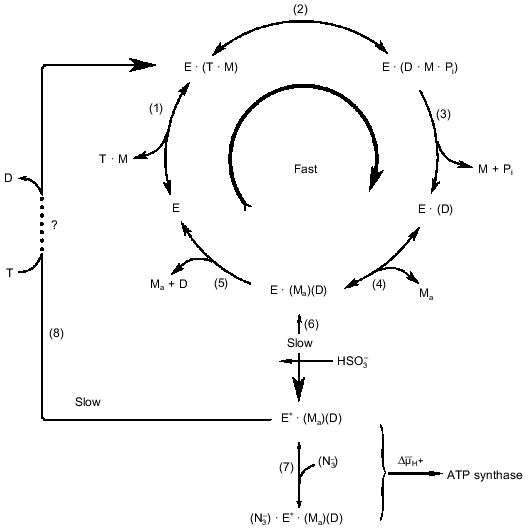
The kinetic data summarized in the table suggest the simplest kinetic scheme for the steady-state ATPase reaction as depicted in Fig. 1. The initial steady-state rate reaction mechanism (under the conditions where slow deactivation of the enzyme is prevented) are shown as the sequence of steps (1)-(5). In addition to what was discussed above, some other comments concerning the reaction sequence is worth mentioning. The participation of free Mg²⁺ corresponds to so-called ping-pong kinetics. Mechanistically this means that "activating" Mg²⁺ participate in the reaction after release of one of the products (ADP or P_i). We believe that P_i leaves the active site before ADP. It is known that P_i is not required for binding of ADP by the enzyme. Also the absence of any inhibitory effect of P_i on F_o·F₁-ATPase suggests that it leaves the enzyme during uncoupled ATP hydrolysis from a site with very low or no affinity and this is taken as the thermodynamic reason for the kinetic sequence of the products release. The simple competitive inhibition of ATPase by free ADP is in accord with the reaction sequence depicted in Fig. 1, where free ADP leaves the catalytic site via a Mg²⁺-dependent mechanism. If the proposal for gamma-subunit Mg²⁺-binding is correct, the structural arrangements of the events shown as the reaction scheme in Fig. 1 would be as follows: free ADP, that is left at the catalytic site after the departure of P_i·Mg, is then released to the solution via an interaction with the Mg²⁺-liganded arm of gamma-subunit. It should be emphasized that the reaction scheme is based an well established fact: the steady-state ATP hydrolysis is described by the simple Michaelis--Menten kinetics [28] as it would be expected if a single substrate-binding site participate in the reaction mechanism. As it was pointed out before, the same behavior is expected if two or more sites participate and high or absolute cooperativity in the catalytic performance exist. The final note is that the proposed kinetic scheme is not aimed to describe the structural rearrangements during the reaction. For example, the release of free ADP by the "magnesium arm" may correspond to the key point of the rotational mechanism with direct interaction between the ADP-containing alpha·beta-subunit and gamma-subunit which sequentially serves alpha·beta pairs.

Fig. 1. Kinetic model of ATP hydrolysis by the mitochondrial ATPase. Reactions (1)-(5) describe the initial steady-state hydrolysis. T, D, M, and M_a stand for ATP, ADP, and Mg²⁺ bound to nucleotide and free (activating) Mg²⁺, respectively. Step (5) is shown as an irreversible reaction because for the initial rate conditions [D] = 0, whereas the irreversibility of step (3) is due to the properties of the catalytic site. The participation of M_a is shown as two separate steps--association, step (4) (pH-dependent binding with pK_a equal to 7.5 [37, 50, 71]), and dissociation, step (5)--for the sake of clarity; the kinetic behavior will be the same if M_a would be permanently bound to one of the enzyme subunits. Steps (6)-(8) describe the slow changes of the enzyme activity (see Section 4). The large curly bracket indicates the intermediates which are subjected to the energy-dependent transformation (see Section 5). The step-by-step mechanism of the ATP-dependent activation of the ADP-deactivated enzyme (8) remains unknown.

4. NON-STEADY-STATE ENZYME KINETICS

Effect of ADP. Mitchell and Moyle were the first to observe a relatively slow time-dependence of some kinetic properties of the ATPase: inhibition by Mg²⁺ and activation by some anions (sulfite) [44, 45]. This phenomenon, although demonstrated for ATPases from a variety of sources [44-47], was somehow ignored for a long time. In 1979, it was discovered in my group that ADP is responsible for the slow transient kinetics of ATPase [25]. Since then, a number of detailed studies have shown that an ADP(Mg²⁺)-dependent slow active/inactive transition is a universal property of F₁-type ATPases. Some essential features of this still enigmatic phenomenon are briefly summarized below.

1. When ATP at relatively low concentrations (<=K_m) is hydrolyzed by ATPase free of protein inhibitor in the absence of an ATP-regenerating system, a rapid decline in the activity is observed which is not due to a decrease in the substrate concentration. Further addition of the enzyme results in a newly observed activity which would be expected if the enzyme added previously have been irreversibly inactivated [25].

2. Brief preincubation of F_o·F₁ (submitochondrial particles) or soluble F₁ with very low, almost stoichiometric concentrations of ADP in the presence of Mg²⁺ results in a considerable lag (in a time scale of minutes) in the onset of ATPase activity measured in the presence of an ATP-regenerating system. Qualitatively the same phenomenon is seen for standard F₁ preparations after preincubation with Mg²⁺ alone, but it is absent when nucleotide-depleted F₁ is assayed with an ATP-regenerating system after preincubation with Mg²⁺ [29, 48].

3. The initial rates of ATP hydrolysis by submitochondrial particles or F₁ measured under unified conditions (with or without regenerating enzymes) are poorly reproducible. The activities are markedly increased and becomes quite reproducible after prolonged preincubation of the preparations in the presence of phosphoenolpyruvate plus pyruvate kinase or phosphocreatine and creatine kinase. After such activation, the ATPase activity measured with an ATP-regenerating system becomes biphasic: a rapid initial phase slowly decreases to 50-70% of the original level, and the reaction then proceeds at a constant rate [29].

4. Neither azide (a specific inhibitor of F₁-ATPase) nor sulfite (activator of the enzyme) affect the initial rapid phase of ATP hydrolysis, whereas the delayed steady-state rate is inhibited by azide and stimulated by sulfite [49]. Hydrolysis of other nucleotides (ITP, GTP) by activated ATPase occurs at a constant rate (no "lags" or "bursts") and is insensitive to azide or sulfite. Preincubation of the enzyme with IDP or GDP has no effect on its ATPase activity, whereas preincubation with ADP completely blocks the initial rates of hydrolysis of the other nucleotides.

5. The duration of the lag-phase in the ATP regeneration assay depends on the ATP concentration approximately in the same way as does the steady-state ATPase activity itself. Thus, activation of the enzyme during preincubation with pyruvate kinase plus phosphoenolpyruvate (no ATP is present, see point 3 above) occurs much more slowly than in the assay system in the presence of added ATP.

6. When ATPase is first deactivated by ADP + Mg²⁺ and then passed through a Sephadex column in the presence of EDTA to remove Mg²⁺, the enzyme becomes "active" and can be deactivated again by added Mg²⁺ [50]. In other words, F_o·F₁ bears a specific site for Mg²⁺ binding with an apparent affinity close to that measured in the steady-state kinetics experiments. Mg²⁺-affinity as revealed by these two independent approaches is strongly pH-dependent. It increases at alkaline pH and decreases upon acidification [37, 50].

7. P_i, which does not affect ATP hydrolysis, strongly modulates the ADP(Mg²⁺)-induced deactivation. It decreases the affinity for ADP at the deactivating site, so that the enzyme can be reactivated equally well either by pyruvate kinase or by P_i [51]. P_i also significantly increases the rate of EDTA-induced activation (see point 6 above) [50].

The results listed above suggest, that in addition to the rapid ATP hydrolytic steady-state turnover route (Fig. 1, steps (1)-(5)), an additional pathway of the enzyme transformation exists (as described in Fig. 1 by steps (6), (7), and (8)), which explains the pre-steady-state kinetics of ATP hydrolysis and also the inhibitory and activating effects of azide and sulfite.

5. UNIDIRECTIONAL TRANSFORMATIONS OF ATPase/SYNTHASE AND REVERSIBILITY OF THE ENZYME OPERATION

ADP dissociates from its ATPase inhibiting site very slowly (the first-order rate constant varies from 0.1 to 1 min^-1). Thus, this site can not be considered as one which participates in the rapid ATPase reaction. Many years ago we showed that ADP(Mg²⁺)-deactivated ATPase is able to catalyze oxidative phosphorylation without any lag in ATP formation [2]. This observation led us to conclude [1, 52, 53] that, when F₁ catalyzes ATP hydrolysis or Deltaµ_H+-dependent ATP synthesis, the enzyme exists in at least two slowly interconvertible conformations. In other words, the microreversibility principle, which is usually quantitatively expressed in enzymology as Haldane relationships does not hold for F₁-ATPase. The main difficulty in obtaining experimental evidence for or against such a proposal is that the conditions for measurement of the reaction in the two directions are quite different. Some recent findings relevant to this problem are briefly discussed below.

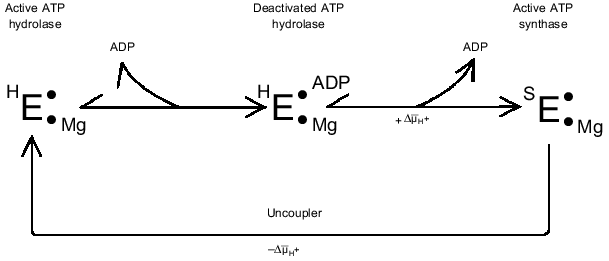
The ADP(Mg²⁺)-deactivated enzyme can be trapped by azide [49] (see Fig. 1, step (7)). Surprisingly, tightly coupled submitochondrial particles in which ADP-deactivated F₁ is trapped by azide catalyze succinate-supported ATP synthesis at the same rate as control samples, whereas both uncoupled ATPase activity and ATP-dependent Deltaµ_H+-generation ceased [53]. Further studies of this unusual unidirectional inhibition have revealed that Deltaµ_H+ ("substrate" or "product" of the reactions) is a strong effector of the F_o·F₁ complex [54]. When ATP synthesis catalyzed by the azide-trapped deactivated enzyme is stopped because of the collapse of Deltaµ_H+, no further hydrolysis of added ATP proceeds. However, if ATP is added first, rapid hydrolysis becomes evident after subsequent addition of an uncoupler to the submitochondrial particles, and the reaction decreased slowly over time because of inhibition by azide. It has been shown that this striking effect of Deltaµ_H+ is not due to back pressure (inhibition by a "product"), and the only ligand that prevents Deltaµ_H+-dependent enzyme transformation is free ADP. Our interpretation of these results is shown in Fig. 2 [54]. The scheme does not describe the detailed mechanism of Deltaµ_H+-dependent transformation of the enzyme. The key point is that the transition ATP hydrolase --> ATP synthase is energy- and ADP-dependent. We observed in our preliminary experiments (unpublished) that the Deltaµ_H+ value needed to transform the enzyme is considerably less than that which is needed as a driving force for ATP synthesis. The "difficult" point in the scheme is that ADP catalyzes the Deltaµ_H+-dependent transition. It may be speculated that this "catalysis" is due to ADP binding at one site and to its Deltaµ_H+-dependent release from another site.

Fig. 2. Deltaµ_H+-dependent transformation of the catalytic activities of F_o·F₁ complex. See text for explanations.

A similar (if not identical) phenomenon of Deltaµ_H+-dependent transformation of ATPase in chloroplasts has been well documented [55-59], and it was interpreted using quite complex kinetic schemes where the coupled ATPase is considered as a "reversible" machine [57]. More recently, our results on the unidirectional inhibition of ATPase activity by azide has been confirmed in the elegant studies on the reconstituted system composed of Thermus thermophilus F_o·F₁-ATP synthase and bacterial rhodopsin [60].

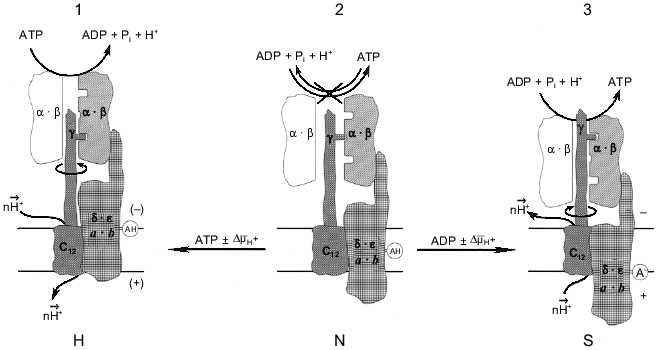
The different reaction pathways for ATP synthesis and hydrolysis catalyzed by F_o·F₁ has been discussed in our previous publications using a language for enzyme kinetics which is not enjoyably acceptable by most scholars in the field. The remarkable progress in structural studies of the enzyme [3, 4] enable us to present our working hypothesis as the scheme shown in Fig. 3. The key point in this scheme is that the "clutch" between a rotating gamma-subunit and alpha₃·beta₃ complex is changed when the enzyme operates in different directions. The simplest driving mechanism to shift the "clutch" from one mode of operation to the other could be the vertical (perpendicular to the plane of the membrane) Deltaµ_H+-dependent movement of one or several subunits of F_o that are firmly attached to the F₁ part. The minimal requirement for such a movement would be the positioning of a charged (or potentially charged) group within the membrane-embedded area to function as a Deltaµ_H+-sensitive sensor. This model is different from those in which elastic spring (gamma-subunit) is proposed for the transmission of a torque from F_o to the catalytic sites of F₁ [15, 61]. I believe that a rigid ratchet mechanism operates in the electromechanical energy transduction. The difficulties which arise when "conformational" energy must be "transported" (which is equivalent to the energy storage in a form of the elastic Young module) were briefly discussed above (see "Introduction"). In my opinion, if Nature has created an electromechanical motor, it has also provided it with a special mechanism to allow it to work effectively as a mechanoelectrical generator, just like similar devices created by mankind are differently constructed although they use the same physical principles when they operate in opposite directions.

Fig. 3. The hypothetical energy-dependent switch-mechanism for F_o·F₁-ATP hydrolase/synthase. For the sake of simplicity F_o·F₁ complex is shown as being composed of three parts. The catalytic part is shown as only one (out of three total) working pair of the alpha·beta-subunits (shadowed). The drive is shown as the proton channel (subunits c) and the gamma-subunit. The third part is a switch-device which is shown as the combination of a-, b-, delta-, and epsilon-subunits. The spatial organization of the subunits is not specified. For detailed information on the structure and dynamics of separate subunits the reader is addressed to an excellent mini-review series published in the Journal of Bioenergetics and Biomembranes [72]. An acidic group AH is shown as an Deltaµ_H+ sensor; a similar model can be easily constructed with a positively charged group. The enzyme state shown in the center corresponds to inactive (incapable of neither hydrolysis nor synthesis) form (N, neutral) in which the proton channel is closed. The synthase state (S) and the hydrolase state (H) are shown on the right and the left, respectively. The different "conformations" may corresponds to the "collapsed" and "extended" states of F_o·F₁ which were described by Green's group many years ago [73]. It is assumed that both S and H states are metastable. Nucleotides participating in the switch mechanism are shown in italic to emphasize their regulatory function. It does not seem to be inconceivable that the binding sites (or type of binding) which are considered as "noncatalytic" sites for ATP hydrolysis operate as "catalytic" sites in the ATP synthesis reaction.

What are the biological advantages of an enzyme operating differently in forward and reverse directions? In a broad sense the answer can be formulated as follows: the separation of the forward and reverse mechanisms is required for improvement of energy transduction efficiency. The term "efficiency" is used here not to mean the ordinary thermal efficiency. It is very hard, if not impossible, to define what is useful for mitochondrion, cell, or whole organism. The quantitative comparison of the thermal efficiencies for some ATP-producing metabolic pathways, such as glycolysis and oxidative phosphorylation, which are often circulated in many biochemistry textbooks, seems to me rather naive. In my understanding the meaning of an "efficiency" is that mitochondria provide the physiologically required rate of ATP synthesis independent of Lipman's phosphoryl potential [62]. On the other hand, an efficient molecular machine must maintain Deltaµ_H+ across the mitochondrial membrane when "glycolytic" ATP is to be used when needed, again independent of phosphoryl potential. The latter appears to occur only under extreme conditions, at least for mammalian cells. An "efficient" ATP synthase should also provide safe electric insulation during its operation. As discussed elsewhere [63, 64], any energy-transducing membrane-bound enzyme is potentially "dangerous" for the others because it contains a proton conducting path. Finally, an efficient machine must be under precise metabolic control. The different mechanisms for forward and reverse reactions make independent metabolic control of the enzyme activities possible, since different conformations of the protein are likely to be susceptible in different ways to the same (or different) ligands. It is well known that different anabolic and catabolic pathways are widely exploited for metabolic regulation in cells. Different enzymes, for example, phosphofructokinase and fructose-bis-phosphatase, operate in glycolysis and gluconeogenesis; again isoenzymes, such as different lactate dehydrogenases, participate in the metabolism of the same substrates in different organs or cell compartments. The rapidly expanding concept that considers an enzyme as a molecular machine makes me think that "the one-way traffic" principal is also realized at the level of a single enzyme. Several recent findings indicate that such a principal applies to another mitochondrial molecular machine, i.e., Complex I of the mitochondrial respiratory chain [64, 65].

6. CONCLUSIONS AND PERSPECTIVES

Tremendous experimental effort has been made for more than half of a century to determine the molecular mechanism of ATP synthesis during oxidative phosphorylation and photophosphorylation. One recent review on the subject contains 284 references, citing almost exclusively papers published since 1990 [66] ! In spite of spectacular progress in the field, it can not be denied that this problem is far from being solved. The great majority of mechanistic studies in the past have been focused on the ATP hydrolysis reaction catalyzed by F₁ which, by definition, is only a hydrolase. An obvious reason for that is that the "synthetic" reaction is far more complex: the Deltaµ_H+-generating system must be included in any assay. Does it mean that we are looking for the lost object exclusively within the illuminated area? Most studies have been performed with explicit or implicit assumption that the enzyme reversibly operates within the F_o·F₁ Deltaµ_H+-dependent ATP synthase complex.

I believe that substantial data have been accumulated in recent years which hardly fit this simple, perhaps unintentionally desired, assumption. Hopefully, in the future, more emphasis will be focused on F_o·F₁ operating in the "physiological direction" (at least for the mammalian enzyme). One may expected that many current dogmas concerning the enzyme mechanism will be reevaluated. After brilliant experiments, where rotation of the gamma-subunit within trimeric alpha·beta pairs composed F₁, was directly visualized [14, 15], the rotary mechanism of F₁ operation comes to be generally accepted. However, it does not seem improbable that the rotation does not occur at all when the complete F_o·F₁ complex operates as a Deltaµ_H+-consuming or Deltaµ_H+-generating device. If some analogy with mechanical machines is to be used, many examples can be found when some part moves reciprocally in the assembled mechanism and it starts to rotate when the device is disassembled. It is hard to predict when the structure of F_o·F₁ at an atomic resolution will be available. Other techniques such as modern cryo-electron microscopy [67, 68] may reveal the Deltaµ_H+-dependent difference in the structure of F_o·F₁ as predicted by the model shown in Fig. 2. Another prediction of the model is that the reactivities and the sites of incorporation for some irreversible inhibitors (nucleotide analogs) are expected to be **Deltaµ_H+-dependent. Perhaps the most direct proof of our hypothesis would be construction of site-directed mutants capable of coupled ATPase and incapable of oxidative phosphorylation (or vise versa). In fact, a recent report on the alpha-subunit mutated thermophilic F₁ [69] strongly support our hypothesis: the mutant catalyzes only the initial rapid phase of ATP hydrolysis (see point 3 in Section 4), whereas this mutated F₁ incorporated (together with bacteriorhodopsin and F_o) into proteoliposomes is perfectly capable of light-induced ATP synthesis [60]!

Enzymatic catalysis is so complex that it is hard to expect formulation of the precise mechanism for any enzyme: the answer concerning a mechanism depends on what particular question is asked. The enzymes are superb because of their catalytic efficiency, specificity and, perhaps most importantly, because of their extremely refined control mechanisms. The later aspect of ATP synthase operation is still at a primitive stage. It hard to believe that "The ATP synthase -- a splendid molecular machine" [70] is not subjected to sophisticated metabolic control.

The work carried out in my laboratory was partially supported by the Russian Foundation for Basic Research (Grants 96-04-48185, 99-04-48082) and by the Program for Advanced Schools in Science (Grant 96-15-97822). I thank all my colleagues past and present for many stimulating discussions. The great help of Mr. F. Kasparinsky and Dr. V. Grivennikova in the preparation of the manuscript is gratefully acknowledged.

REFERENCES

1.Vinogradov, A. D. (1984) Biokhimiya, 49, 1220-1238.
2.Minkov, I. B., Vasilyeva, E. A., Fitin, A. F., and Vinogradov, A. D. (1980) Biochem. Int., 1, 478-485.
3.Abrahams, J. P., Leslie, A. G. W., Lutter, R., and Walker, J. E. (1994) Nature, 370, 621-628.
4.Bianchet, M. A., Hullihen, J., Pedersen, P. L., and Amzel, L. M. (1998) Proc. Natl. Acad. Sci. USA, 95, 11065-11070.
5.Fillingame, R. H. (1997) J. Exp. Biol., 200, 217-224.
6.Gresser, M. J., Myers, J. A., and Boyer, P. D. (1982) J. Biol. Chem., 257, 12030-12038.
7.Grubmeyer, C., Cross, R. L., and Penefsky, H. S. (1982) J. Biol. Chem., 257, 12092-12100.
8.Grubmeyer, C., and Penefsky, H. S. (1981) J. Biol. Chem., 256, 3728-3734.
9.Boyer, P. (1993) Biochim. Biophys. Acta, 1140, 215-250.
10.Boyer, P. (1998) Biosci. Reports, 18, 97-117.
11.Duncan, T. M., Bulygin, V. V., Zhou, Y., Hutcheon, M. L., and Cross, R. (1995) Proc. Natl. Acad. Sci. USA, 92, 10964-10968.
12.Sabbert, D., Engelbrecht, S., and Junge, W. (1996) Nature, 381, 623-625.
13.Junge, W., Sabbert, D., and Engelbrecht, S. (1996) Ber. Bunsenges. Phys. Chem., 100, 2014-2019.
14.Noji, H., Yasuda, R., Yoshida, M., and Kinoshita, K. (1997) Nature, 386, 299-302.
15.Yasuda, R., Noji, H., Kinoshita, K., and Yoshida, M. (1998) Cell, 93, 1117-1124.
16.Ishlinskii, A. Yu. (ed.) (1989) Engineering and Technology Dictionary [in Russian], 3rd ed., Sovetskaya Entsiklopediya, Moscow.
17.Feynman, R. P., Leighton, R. B., and Sands, M. (1963) in The Feynman Lectures on Physics, Vol. 1, Chap. 46, Addison-Wesley Publishing Company, Inc. Massachusetts.
18.Pullman, M. E., and Monroy, G. C. (1963) J. Biol. Chem., 238, 3762-3769.
19.Panchenko, M. V., and Vinogradov, A. D. (1989) Biokhimiya, 54, 569-579.
20.Panchenko, M. V., and Vinogradov, A. D. (1985) FEBS Lett., 184, 226-230.
21.Vasilyeva, E. A., Panchenko, M. V., and Vinogradov, A. D. (1989) Biokhimiya, 54, 1490-1498.
22.Yamada, E. W., and Huzel, N. J. (1988) J. Biol. Chem., 263, 11498-11503.
23.Akimenko, V. K., Minkov, I. B., Bakeeva, L. E., and Vinogradov, A. D. (1972) Biokhimiya, 37, 348-358.
24.Hammes, G. G., and Hilborn, D. A. (1971) Biochim. Biophys. Acta, 233, 580-590.
25.Fitin, A. F., Vasilyeva, E. A., and Vinogradov, A. D. (1979) Biochem. Biophys. Res. Commun., 86, 434-439.
26.Jault, J.-M., and Allison, W. S. (1994) J. Biol. Chem., 269, 319-325.
27.Yokoyama, K., Muneyuki, E., Amano, T., Mizutani, S., Yoshida, M., Ishida, M., and Ohkuma, S. (1998) J. Biol. Chem., 273, 20504-20510.
28.Vasilyeva, E. A., Fitin, A. F., Minkov, I. B., and Vinogradov, A. D. (1980) Biochem. J., 188, 807-815.
29.Vasilyeva, E. A., Minkov, I. B., Fitin, A. F., and Vinogradov, A. D. (1982) Biochem. J., 202, 9-14.
30.Selwyn, M. J. (1967) Biochem. J., 105, 279-288.
31.Alexander, A., Carignani, G., and Rossi, C. A. (1975) FEBS Lett., 52, 111-115.
32.Shuster, S. M., Ebel, R. E., and Lardy, H. A. (1975) J. Biol. Chem., 250, 7848-7853.
33.Wong, S. Y., Matsuno-Yagi, A., and Hatefi, Y. (1984) Biochemistry, 23, 5004-5010.
34.Lazdunski, M. (1972) in Current Topics in Cellular Regulation (Horecker, B. L., and Stadman, E. R., eds.) Vol. 6, Academic Press, New York-London, pp. 267-278.
35.Repke, K. R. H., and Schön, R. (1973) Acta Biol. Med. Germ., 31, k19-k30.
36.Repke, K. R. H., and Schön, R. (1974) Acta Biol. Med. Germ., 33, k27-k38.
37.Syroeshkin, A. V., Galkin, M. A., Sedlov, A. V., and Vinogradov, A. D. (1999) Biochemistry (Moscow), 64, 1128-1137.
38.Galkin, M. A., and Syroeshkin, A. V. (1999) Biochemistry (Moscow), 64, 1176-1185.
39.Zhou, J.-M., and Boyer, P. D. (1992) Biochemistry, 31, 3166-3171.
40.Penefsky, H. S. (1977) J. Biol. Chem., 252, 2891-2899.
41.Kasahara, M., and Penefsky, H. S. (1978) J. Biol. Chem., 253, 4180-4187.
42.Fleury, B., di Pietro, A., Godinot, C., and Gautheron, D. C. (1980) Biochimie, 62, 733-737.
43.Lutter, R., Abrahams, J. P., van Raaij, M. J., Todd, R. J., Lundqvist, T., Buchanan, S. K., Leslie, A. G. W., and Walker, J. E. (1993) J. Mol. Biol., 229, 787-790.
44.Mitchell, P., and Moyle, J. (1971) Bioenergetics, 2, 1-11.
45.Moyle, J., and Mitchell, P. (1975) FEBS Lett., 56, 55-61.
46.Recktenwald, D., and Hess, B. (1977) FEBS Lett., 80, 187-189.
47.Recktenwald, D., and Hess, B. (1979) FEBS Lett., 108, 257-260.
48.Minkov, I. B., Fitin, A. F., Vasilyeva, E. A., and Vinogradov, A. D. (1979) Biochem. Biophys. Res. Commun., 89, 1300-1306.
49.Vasilyeva, E. A., Minkov, I. B., Fitin, A. F., and Vinogradov, A. D. (1982) Biochem. J., 202, 15-23.
50.Bulygin, V. V., and Vinogradov, A. D. (1991) Biochem. J., 276, 149-156.
51.Yalamova, M. V., Vasilyeva, E. A., and Vinogradov, A. D. (1982) Biochem. Int., 4, 337-344.
52.Vinogradov, A. D., Vasilyeva, E. A., and Evtushenko, O. A. (1985) Proc. 16th FEBS Congr., Part B, VNU Science Press, pp. 291-299.
53.Syroeshkin, A. V., Vasilyeva, E. A., and Vinogradov, A. D. (1995) FEBS Lett., 366, 29-32.
54.Galkin, M. A., and Vinogradov, A. D. (1999) FEBS Lett., 448, 123-126.
55.Junge, W. (1970) Eur. J. Biochem., 14, 582-592.
56.Du, Z., and Boyer, P. D. (1989) Biochemistry, 28, 873-879.
57.Gräber, P. (1994) Biochim. Biophys. Acta, 1187, 171-176.
58.Zhou, J.-M., and Boyer, P. D. (1993) J. Biol. Chem., 268, 1531-1538.
59.Groth, G., and Junge, W. (1995) FEBS Lett., 358, 142-144.
60.Bald, D., Amano, T., Muneyuki, E., Pitard, B., Rigaud, J.-L., Kruip, J., Hisabori, T., Yoshida, M., and Shibata, M. (1998) J. Biol. Chem., 273, 865-870.
61.Cherepanov, D. A., Mulkidjanian, A. Y., and Junge, W. (1999) FEBS Lett., 449, 1-6.
62.Lipmann, F. (1960) in Molecular Biology (Nachmansohn, D., ed.) Academic Press, New York, pp. 49-61.
63.Maklashina, E. O., Sled, V. D., and Vinogradov, A. D. (1994) Biochemistry (Moscow), 59, 707-714.
64.Vinogradov, A. D. (1998) Biochim. Biophys. Acta, 1364, 169-185.
65.Vinogradov, A. D., Gavrikova, E. V., Grivennikova, V. G., Zharova, T. V., and Zakharova, N. V. (1999) Biochemistry (Moscow), 64, 136-152.
66.Weber, J., and Senior, A. E. (1997) Biochim. Biophys. Acta, 1319, 19-58.
67.Gogol, E. P., Johnston, E., Aggeler, R., and Capaldi, R. A. (1990) Proc. Natl. Acad. Sci. USA, 87, 9585-9589.
68.Singh, S., Turina, P., Bustamante, C. J., Keller, D. J., and Capaldi, R. (1996) FEBS Lett., 397, 30-34.
69.Matsui, T., Muneyuki, E., Honda, M., Allison, W. S., Dou, C., and Yoshida, M. (1997) J. Biol. Chem., 272, 8215-8221.
70.Boyer, P. (1997) Annu. Rev. Biochem., 66, 717-749.
71.Bulygin, V. V., Syroeshkin, A. V., and Vinogradov, A. D. (1993) FEBS Lett., 328, 193-196.
72.Pedersen, P. L. (ed.) (1996) J. Bioenerg. Biomembr., 28.
73.Hatase, O., Wakabayashi, T., Hayashi, H., and Green, D. E. (1972) J. Bioenerg., 3, 509-514.

---