Kinetics of Heat Aggregation of Proteins
B. I. Kurganov
Bakh Institute of Biochemistry, Russian Academy of Sciences, Leninskii pr. 33, Moscow, 117071 Russia; fax: (095) 954-2732; E-mail: inbio@glas.apc.org
Received January 26, 1998
The mechanism of heat aggregation of proteins proposed by the author involves the stage of irreversible denaturation, the stage of nucleation, and the stage of growth of aggregates. It was shown that the initial parts of the kinetic curves of aggregation followed by monitoring the increase in absorbance (A) or intensity of light scattering (I) are linearized in coordinates {dA/dt; t} and {A; t2} (or, respectively, in coordinates {dI/dt; t} and {I; t2}). The slope of these linear anamorphoses is proportional to the product of the rate constant of irreversible denaturation and the rate constant of growth of aggregates. The mechanism of heat aggregation proposed is fulfilled for pig heart citrate synthase. The dI/dt versus t curves for heat aggregation of glycogen phosphorylase b from rabbit skeletal muscles display a lag period whose appearance is caused by intramolecular predenaturational changes in the enzyme molecule.
KEY WORDS: protein aggregation, denaturation, citrate synthase, glycogen phosphorylase
Heat denaturation of proteins is often accompanied by aggregation of denatured protein molecules [1]. Accumulation of aggregates may be easily registered by monitoring the increase in absorbance or intensity of light scattering. The great interest of biochemists to protein aggregation is due to intensive investigations of folding of proteins which are being done at the present time. Aggregation of partially folded polypeptide chains decreases markedly the yield of the final product of the folding process--a native conformer possessing a biological activity. The cell contains special proteins, molecular chaperons, which are able to bind partly folded polypeptide chains and facilitate their folding to the native conformation [2]. The study of the influence of chaperon-like proteins (for example, heat shock proteins) on heat aggregation of model proteins is considered as one of the tests for chaperon-like activity. It is evident that in order to interpret the results being obtained the experimenter must have in his disposal the methods of quantitative estimation of the effect of chaperon-like proteins on the rate of aggregation of a model protein. In the present paper we have proposed the mechanism of heat aggregation of proteins which allows the initial parts of the kinetic curves of aggregation to be quantitatively described.
The mechanism of heat aggregation under discussion involves the following stages. The initial stage is denaturation of a protein which is considered for the sake of simplicity as an irreversible reaction
kden
N --> D (1)
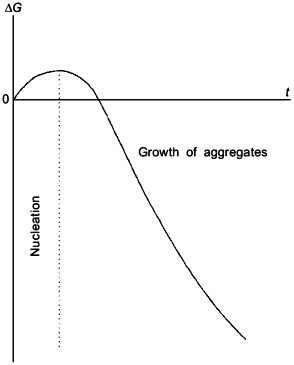
In order to describe the kinetics of aggregation of denatured molecules of a protein, we have used a theory of protein aggregation proposed by Patro and Przybycien [3]. It is the authors’ opinion that the initial stages of reversible protein aggregation involve the reaction of nucleation and the reaction of growth of aggregates (Fig. 1). The stage of nucleation is thermodynamically unfavorable (the change of free energy, DeltaG, is positive) because of the loss in configurational entropy. When the aggregating phase contains a sufficient number of stable nuclei, the system reaches a critical state beyond which "monomer" D addition is favorable, leading to decrease in the system free energy. We can write the stage of nucleation and the stage of growth of aggregates as follows:
| kagg |
| Dn + D --> Dn+1 (3) |
(n is the number of "monomers" D participating in the formation of a nucleus and kagg is the rate constant for the stage of growth of aggregates). We ignore the reversibility of aggregation since our main interest is the initial rate of aggregation.
At sufficiently low values of time (t) the accumulation of denatured form D proceeds linearly in time: [D] = kden[N]0t ([N]0 is the initial concentration of the protein). For initial parts of the kinetic curves a registered value of absorbance A (or intensity of light scattering I) is proportional to the amount of aggregates formed and the rate of the change in the A value, dA/dt, is proportional to the product kagg[D] (assuming that the nuclei concentration is constant). Taking into account the linear character of accumulation of the form D, we obtain that dA/dt proportional to kdenkagg[N]0t (4). Thus, with the above assumptions the kinetic curves of aggregation should be linearized in coordinates {dA/dt; t}, the slope of the straight line in these coordinates being proportional to the product kdenkagg[N]0. Integration of Eq. (4) shows that at sufficiently low values of time the A value is proportional to t2: A proportional to kdenkagg[N]0t2. It should be noted that after the completion of the stage of nucleation the process of heat protein aggregation is essentially described by reactions (1) and (3).Fig. 1. Free energy change (DeltaG) as a function of time (t) for the initial stages of reversible protein aggregation [3].
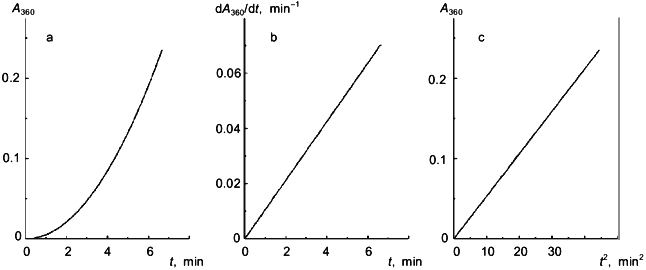
Pig heart citrate synthase (EC 4.1.3.7) is a dimeric enzyme (Mr = 96 kD) which is used in many works as a model protein suitable for the estimation of chaperon-like activity of the proteins under study. The loss in the enzymatic activity of citrate synthase at elevated temperatures follows the exponential law [4-6]. A typical kinetic curve of heat aggregation of citrate synthase is presented in Fig. 2a. As can be seen from Figs. 2b and 2c, the kinetic curves are linearized in coordinates {dA/dt; t} and {A; t2}. An analogous conclusion was made by us when analyzing the data on citrate synthase aggregation obtained by Buchner and coworkers [4-6]. Thus, the kinetics of aggregation of citrate synthase follows the mechanism of protein aggregation proposed by us. The slope of the straight line in coordinates {dA/dt; t} or {A; t2} is proportional to the product of the rate constants kden and kagg. In the case of testing the specific ligands which are able to interact with the native form N (for example, for testing the substrate, oxalacetic acid, revealing marked stabilizing effect), the change in the slope of the straight line in the above coordinates is due to the change in the value of the rate constant kden. At the same time, in the case of testing the chaperon-like proteins which do not interact with the native protein and do not affect the inactivation rate of citrate synthase (for example, for testing Hsp25 [6], the component of Hsp90, FKBP52 [5], and Hsp 16.3 [7]), the change in the slope of the straight line in the above coordinates is caused by the alteration of the rate constant kagg.
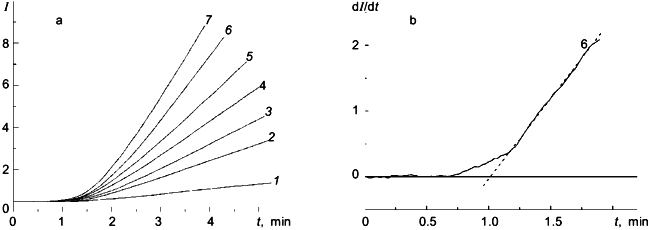
The kinetics of heat aggregation of another dimeric enzyme--glycogen phosphorylase b (Mr = 194.8 kD) from rabbit skeletal muscles--are more complex. As can be seen from Fig. 3a, the initial parts of the kinetic curves obtained at various initial concentrations of the enzyme [E]0 have a delayed character. This conclusion is confirmed by the construction of dI/dt versus t plots (I is intensity of light scattering). As an example, Fig. 3b shows a kinetic curve constructed in coordinates {dI/dt; t} at [E]0 = 0.93 mg/ml. Since the current value of the derivative dI/dt is proportional to the current concentration of the denatured form D, the appearance of a lag period on the dI/dt versus t curves means that the formation of the form D is preceded by the predenaturational changes in the phosphorylase b molecule. The slope of the linear part of the dependence of dI/dt on t after the passing of a lag period (designated by us as w0) is proportional to the rate of accumulation of the D form. The duration of the lag period (tau) is independent of the enzyme concentration, and the value of w0 increases linearly with increasing the [E]0 value. In accordance with the theory of dissociating enzyme systems [9] such a character of the dependences of the tau and w0 values on [E]0 indicates that the predenaturational changes in the phosphorylase b molecule are not associated with the processes of dissociation-association of protein molecules.Fig. 2. Heat aggregation of pig heart citrate synthase. a) Time-course of the increase in absorbance at 360 nm, A360 (50 mM Hepes, pH 7.0; 39.5°C) [7]. b, c) Linear anamorphoses in coordinates {dA360/dt; t} and {A360; t2}, respectively.
This study was funded by grants 96-04-50819 and 96-04-10016C from the Russian Foundation for Basic Research.Fig. 3. Heat aggregation of phosphorylase b from rabbit skeletal muscles. a) Dependences of intensity of light scattering (I) at 600 nm on time obtained at the following values of the enzyme concentration [E]0 (mg/ml): 1)0.17;2) 0.35;3) 0.46; 4) 0.58;5) 0.70;6) 0.93;7) 1.16(80 mM Hepes, pH 6.8; 53°C) [8]. b) Linear anamorphosis in coordinates {dI/dt; t} at [E]0 = 0.93 mg/ml.
REFERENCES
1.Joly, M. (1965) A Physicochemical Approach to
the Denaturation of Proteins, Academic Press, New York, pp.
153-170.
2.Martin, J., and Hartl, F. U. (1997) Curr. Opin.
Struct. Biol., 7, 41-52.
3.Patro, S. Y., and Przybycien, T. M. (1996)
Biophys. J., 70, 2888-2902.
4.Jakob, U., Lilie, H., Meyer, I., and Buchner, J.
(1995) J. Biol. Chem., 270, 7288-7294.
5.Bose, S., Weikl, T., and Buchner, J. (1996)
Science, 274, 1715-1717.
6.Ehrnsperger, M., Gräber, S., Gaestel, M., and
Buchner, J. (1997) EMBO J., 16, 221-229.
7.Chang, Z., Primm, T. P., Jakana, J., Lee, I. H.,
Serysheva, I., Chiu, W., Gilbert, H. F., and Quiocho, F. A. (1996)
J. Biol. Chem., 271, 7218-7223.
8.Kornilaev, B. A., Kurganov, B. I., Eronina, T. B.,
Chebotareva, N. A., Livanova, N. B., Orlov, V. N., and Chernyak, V. Ya.
(1997) Mol. Biol. (Moscow), 31, 82-89.
9.Kurganov, B. I. (1978) Allosteric Enzymes.
Kinetic Behaviour, J. Wiley and Sons, Chichester, pp. 151-313.